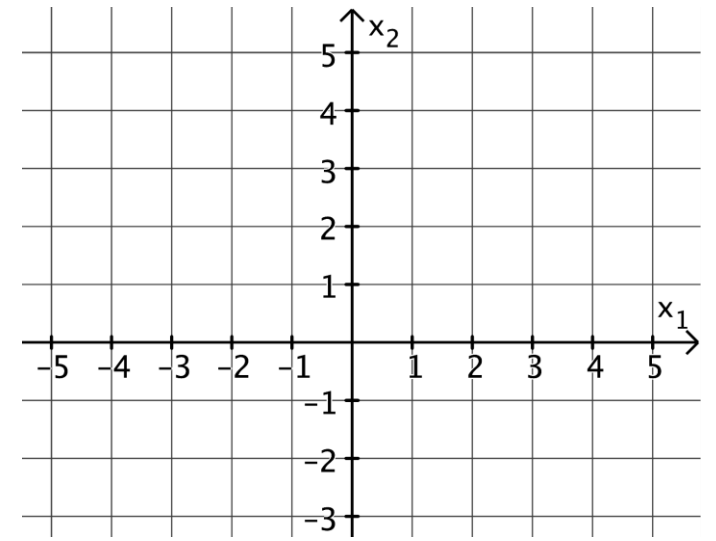
Verschiebt man jeden der Punkte $𝐴,𝐵,𝐶,𝐷$ und $𝑀$ parallel zur ${𝑥}_3$-Achse in die

$x_1{x}_2$-Ebene, so ergeben sich die Punkte $A^{\prime },B^{\prime },C^{\prime },D^{\prime }$ bzw. $M^{\prime }$. Das Viereck $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ ist ein Parallelogramm, dessen Diagonalen sich im Punkt $M^{\prime }$ schneiden. Zeichnen Sie das Viereck $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ und $M^{\prime }$ in die Abbildung ein. [3 BE]

Berechnen Sie den Wert des Skalarprodukts $\overrightarrow{CM}\circ \overrightarrow{CB}=\left(\begin{array}{c}1\\ -2\\ -9\end{array}\right)\circ \left(\begin{array}{c}2\\ -1\\ 2\end{array}\right)$ und beurteilen Sie, ob der Winkel zwischen den Vektoren $\overrightarrow{CM}$ und $\overrightarrow{CB}$ kleiner als ${90}^{\circ }$ ist.

[2 BE]