Aufgabe P3
Die Punkte , , und sind Eckpunkte des in der Abbildung dargestellten Quaders .
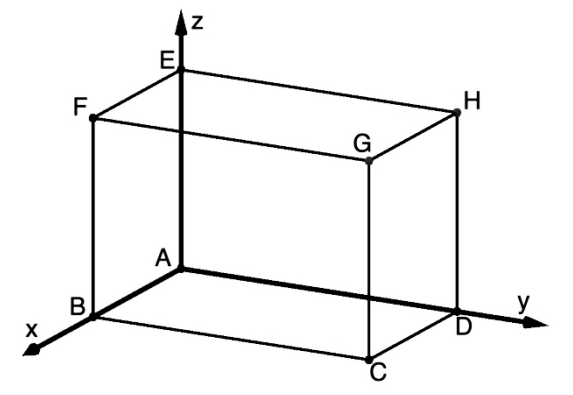
Geben Sie die Koordinaten des Punktes an. [1 BE]
Der Quader wird so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen im Koordinatenursprung befindet. Dabei entsteht der Quader .
Ermitteln Sie die Koordinaten des Punkts . [3 BE]
Geben Sie einen Eckpunkt des Quaders an, der nur positive Koordinaten hat. [1 BE]
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
serlo.orgDieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
→ Was bedeutet das?