Pflichtteil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

1
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P1
Gegeben ist die in $R$ definierte Funktion $f$ mit $f (x) = x^{3} - 4 x$ .
1. Begründen Sie, dass der Graph von $f$ symmetrisch bezüglich des Koordinatenursprungs ist. [1 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punktsymmetrie
  Der Graph von $f$ ist symmetrisch bezüglich des Koordinatenursprungs
  Der Funktionsterm enthält nur ungerade Exponenten, d.h. der Graph von $𝑓$ ist symmetrisch bezüglich des Koordinatenursprungs.
  Alternativ:
  $f (- x) = (- x)^{3} - 4 (- x) = - x^{3} + 4 x = - (x^{3} - 4 x) = - f (x)$
  Aus $f (- x) = - f (x)$ folgt, dass der Graph von $𝑓$ symmetrisch bezüglich des Koordinatenursprungs ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte die Potenzen von $x$ .
2. Der Graph von $f$ und die x-Achse schließen eine Fläche ein, die aus zwei Flächenstücken besteht. Berechnen Sie den Inhalt dieser Fläche. [4 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Berechne den Inhalt dieser Fläche
  Für die Flächenberechnung werden die Nullstellen der Funktion benötigt.
  $0=x(x^2-4)\;\Rightarrow\;x_1=0$ und $x_{2{,}3}=\pm2$
  Im Intervall $[- 2; 0]$ ist $f(x)\geq0$ und wegen der Punktsymmetrie bezüglich des Koordinatenursprungs gilt dann:
  $A=2\cdot\displaystyle\int_{-2}^0f(x)\;\mathrm{d}x=2\cdot\left[\dfrac{1}{4}x^4-2x^2\right]_{-2}^0=2\cdot(0-(4-8))=8$
  Der Inhalt dieser Fläche beträgt $8\; \text{FE}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Nullstellen der Funktion und beachte die Punktsymmetrie des Graphen von $f$ bezüglich des Koordinatenursprungs.
2
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P2
Bei einer Werbeaktion erhält jedes Kind einen blickdicht verpackten Ball. Die Wahrscheinlichkeit dafür, dass dieser Ball rot ist, beträgt $40 %$ .
1. Zeigen Sie, dass die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen roten Ball erhält, kleiner als $10 %$ ist. [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen roten Ball erhält, ist kleiner als $10 %$
  Gegeben ist $p_{\text{rot}}=0{,}4$ .
  Gesucht ist die Wahrscheinlichkeit $P (X = 3)$ :
  $P(X=3)=0{,}4^3=0{,}064<0{,}1$
  Damit ist $P(X=3)<10\; \%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $P (X = 3)$ mit $p = 0,4$ und $n = 3$ .
2. Beschreiben Sie im Sachzusammenhang ein Zufallsexperiment, bei dem die
  Wahrscheinlichkeit eines Ereignisses mit dem Term $1 ⋅ 0{,}4^0⋅ 0{,}6^4 + 4 ⋅ 0{,}4^1⋅ 0{,}6^3$ berechnet werden kann. Geben Sie dieses Ereignis an. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Gib dieses Ereignis an
  Der Term $1 ⋅ 0{,}4^0⋅ 0{,}6^4 + 4 ⋅ 0{,}4^1⋅ 0{,}6^3$ beschreibt die Wahrscheinlichkeit eines Zufallsexperiments.
  $1 ⋅ 0{,}4^0⋅ 0{,}6^4$ ist die Wahrscheinlichkeit dafür, dass von $4$ Kindern keines einen roten Ball erhält.
  $4 ⋅ 0{,}4^1⋅ 0{,}6^3$ ist die Wahrscheinlichkeit dafür, dass $1$ Kind (von den $4$ Kindern) einen roten Ball erhält.
  Somit beschreibt der angegebene Term folgendes Zufallsexperiment:
  Vier Kinder erhalten jeweils einen Ball.
  Das Ereignis lautet dann: "Höchstens einer der Bälle ist rot".
  Hinweis: der angegebene Term lässt sich auch so schreiben:
  $\displaystyle 1 \cdot 0{,}4^0⋅ 0{,}6^4 + 4 \cdot 0{,}4^1⋅ 0{,}6^3=\binom{4}{0}p_\text{rot}^0\cdot (1-p_\text{rot})^4+\binom{4}{1}p_\text{rot}^1\cdot (1-p_\text{rot})^3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Untersuche getrennt die beiden Teile des angegebenen Terms.
3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P3
Die Punkte $A (0 ∣ 0 ∣ 0)$ , $B (3 ∣ 0 ∣ 0)$ , $E (0 ∣ 0 ∣ 4)$ und $H (0 ∣ 6 ∣ 4)$ sind Eckpunkte des in der Abbildung dargestellten Quaders $A B C D E F G H$ .
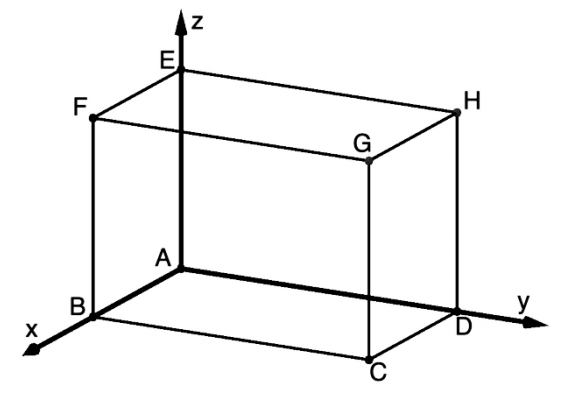
1. Geben Sie die Koordinaten des Punktes $G$ an. [1 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Das Koordinatensystem
  Gib die Koordinaten des Punktes $G$ an
  $G$ hat dieselbe $x$ -Koordinate wie $B$ , dieselbe $y$ -Koordinate wie $H$ und dieselbe $z$ -Koordinate wie $H$ .
  Die Koordinaten des Punktes $G$ lauten: $G (3 ∣ 6 ∣ 4)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege Dir anhand der gegebenen Koordinaten, welche Koordinaten der Punkt $G$ hat.
2. Der Quader wird so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen im Koordinatenursprung befindet. Dabei entsteht der Quader $A^{'} B^{'} C^{'} D^{'} E^{'} F^{'} G^{'} H^{'}$ .
  Ermitteln Sie die Koordinaten des Punkts $H^{'}$ . [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden
  Ermittle die Koordinaten des Punktes $H^{'}$
  Für die Koordinatenermittlung von $H^{'}$ wird der Schnittpunkt $S$ der beiden Raumdiagonalen des Quaders benötigt.
  Dieser Schnittpunkt $S$ ist der Mittelpunkt der Strecke $\overline{B H}$ .
  $\overrightarrow{O S}=\dfrac{1}{2}\cdot\left(\overrightarrow{O B}+\overrightarrow{O H}\right)=\dfrac{1}{2}\cdot\left(\begin{pmatrix}3\\0\\0\end{pmatrix}+\begin{pmatrix}0\\6\\4\end{pmatrix}\right)=\dfrac{1}{2}\cdot\begin{pmatrix}3\\6\\4\end{pmatrix}=\begin{pmatrix}1{,}5\\3\\2\end{pmatrix}$
  Somit gilt: $S (1,5 ∣ 3 ∣ 2)$ .
  Der Quader wird so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen $S$ im Koordinatenursprung befindet.
  $\Rightarrow\;\overrightarrow{OH'}=\overrightarrow{OH}-\overrightarrow{OS}=\begin{pmatrix}0\\6\\4\end{pmatrix}-\begin{pmatrix}1{,}5\\3\\2\end{pmatrix}=\begin{pmatrix}-1{,}5\\3\\2\end{pmatrix}$
  Die Koordinaten des Punkts $H^{'}$ lauten $(- 1,5 ∣ 3 ∣ 2)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für die Koordinatenermittlung von $H^{'}$ wird der Schnittpunkt der beiden Raumdiagonalen des Quaders benötigt. Dieser Schnittpunkt $S$ ist der Mittelpunkt der Strecke $\overline{B H}$ . Berechne $S$ .
  Der Quader wird so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen $S$ im Koordinatenursprung befindet.
  $\overrightarrow{OH'}=\overrightarrow{OH}-\overrightarrow{OS}$
3. Geben Sie einen Eckpunkt des Quaders $A^{'} B^{'} C^{'} D^{'} E^{'} F^{'} G^{'} H^{'}$ an, der nur positive Koordinaten hat. [1 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quader
  Gib einen Eckpunkt des Quaders $A^{'} B^{'} C^{'} D^{'} E^{'} F^{'} G^{'} H^{'}$ an, der nur positive Koordinaten hat
  Der Punkt $G$ des Quaders wird bei der Verschiebung auf den Punkt $S$ geschoben. $S$ hat die Koordinaten $(1,5 ∣ 3 ∣ 2)$ . Somit hat $G^{'}$ nun die Koordinaten von $S$ , die alle positiv sind.
  Der Punkt $G^{'}$ ist der gesuchte Eckpunkt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Punkt $S$ hat z.B. nur positive Koordinaten. Überlege Dir, welcher Punkt bei der Verschiebung des Quaders auf $S$ fällt.
4
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe Q1
Die Abbildung zeigt den Graphen $𝐺_{𝑓}$ einer in $R$ definierten Funktion $𝑓$ .
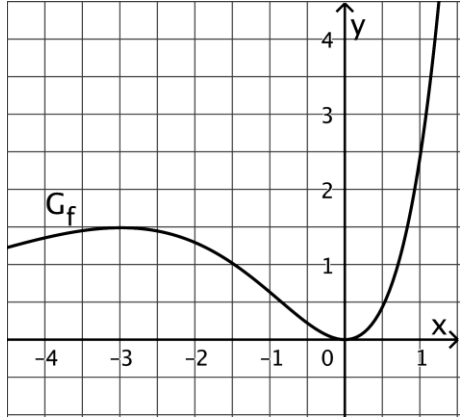
1. Bestimmen Sie grafisch den Wert des Integrals $\displaystyle\int^{−1{,}5}_{−3} f(x)\;\mathrm{d}x$ . [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Bestimme grafisch den Wert des Integrals
  Man zählt die Kästchen zwischen dem Graphen von $f$ und der x-Achse im Bereich von $- 3$ bis $- 1,5$ . Es sind etwa $8$ Kästchen.
  $4$ Kästchen ergeben eine Einheit, d.h. der Wert des Integrals $\displaystyle\int^{−1{,}5}_{−3} f(x)\;\mathrm{d}x$ ist etwa $2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zähle die Kästchen zwischen dem Graphen von $f$ und der x-Achse im Bereich von $- 3$ bis $- 1,5$ .
2. Beschreiben Sie, wie der Graph der in $R$ definierten Funktion $u$ mit $u (𝑥) = - f (𝑥) + 2$ aus $𝐺_{f}$ erzeugt werden kann.
  Geben Sie die Koordinaten des Hochpunkts des Graphen von $u$ an. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Transformationen von Funktionen
  Beschreibe, wie der Graph der in $R$ definierten Funktion $u$ mit $𝑢 (𝑥) = - 𝑓 (𝑥) + 2$ aus $𝐺_{𝑓}$ erzeugt werden kann
  $f(x)\xrightarrow{\text{Spiegelung an der x-Achse}}-f(x)\xrightarrow{\text{Verschiebung um 2 in positive y-Richtung}}-f(x)+2$
  Gib die Koordinaten des Hochpunkts des Graphen von $𝑢$ an
  Wird der Graph an der x-Achse gespiegelt, dann wird der Hochpunkt $(- 3 ∣ 1,5)$ zum Tiefpunkt und der Tiefpunkt $(0 ∣ 0)$ wird zum Hochpunkt.
  Nun muss der Graph noch um $2$ in positive y-Richtung verschoben werden, sodass der Hochpunkt nun die Koordinaten $(0 ∣ 2)$ hat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  $- f (x)$ entspricht einer Spiegelung an der x-Achse. $+ 2$ verschiebt den Graphen um 2 nach oben.
  Teil 2
  Spiegele den Graphen an der x-Achse und verschiebe ihn um $2$ nach oben. Dann kann man die Koordinaten des Hochpunkts ablesen.
5
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe Q2
Im hinteren Teil eines Klassenzimmers stehen sechs Stühle in einer Reihe.
1. Es gibt vier Möglichkeiten, drei der sechs Stühle so auszuwählen, dass zwischen je zwei ausgewählten Stühlen mindestens ein weiterer Stuhl steht.
  Geben Sie diese Möglichkeiten an. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kombinatorik
  Gib diese Möglichkeiten an
  Die $4$ Möglichkeiten, drei der sechs Stühle so auszuwählen, dass zwischen je zwei ausgewählten Stühlen mindestens ein weiterer Stuhl steht, sind in der folgenden Abbildung dargestellt.
  Die schwarzen Kreise zeigen die ausgewählten Stühle an.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Male Dir $4$ Reihen mit jeweils $6$ Kästchen und markiere die besetzten Stühle.
2. Die Schüler Aaron, Bert und Can sollen sich so auf jeweils einen der sechs Stühle setzen, dass zwischen je zwei Schülern mindestens ein weiterer Stuhl steht.
  Berechnen Sie, wie viele Möglichkeiten es dafür gibt. [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kombinatorik
  Berechne, wie viele Möglichkeiten es dafür gib
  $3!$ ist die Anzahl für die Anordnung von $3$ Personen.
  Da es $4$ Reihen sind (siehe Aufgabe a), folgt für die gesamte Anzahl $n$ der Möglichkeiten: $n=4\cdot3!=24$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Drei Personen können auf $3!$ Arten angeordnet werden.
  Beachte, wie viele Reihen es in der Aufgabe a) gibt

Aufgabe Q3

Gegeben sind die Punkte $P (2 ∣ 0 ∣ 23)$ und $Q_{t} (6 ∣ 𝑡 ∣ 20)$ mit $t ∈ \mathbb{R}$ .

Entscheiden Sie, ob es einen Wert von $t$ gibt, für den die Gerade $P Q_{t}$ parallel zur xy-Ebene verläuft.
Begründen Sie Ihre Entscheidung. [2 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
Gibt es einen Wert von $t$ , für den die Gerade $P Q_{t}$ parallel zur xy-Ebene verläuft
Es gibt keinen solchen Wert für $t$ , da $P$ und $Q_{t}$ für alle $t$ unterschiedliche z-Koordinaten haben.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Vergleiche die z-Koordinaten der Punkte $P$ und $Q_{t}$ .

Der Koordinatenursprung und die Punkte $P$ und $Q_{t}$ bilden ein Dreieck.

Ermitteln Sie diejenigen Werte von $T$ , für die das Dreieck in $Q_{t}$ einen rechten Winkel hat. [3 BE]

7
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe R1
Gegeben ist die in $\mathbb{R}$ definierte Funktion f mit $f(x) =\frac{1}{2}⋅ x^2$
Die Abbildung zeigt den Graphen von $f$ sowie die Tangente $t$ an den Graphen von $f$ im Punkt $(4 ∣ f (4))$ .
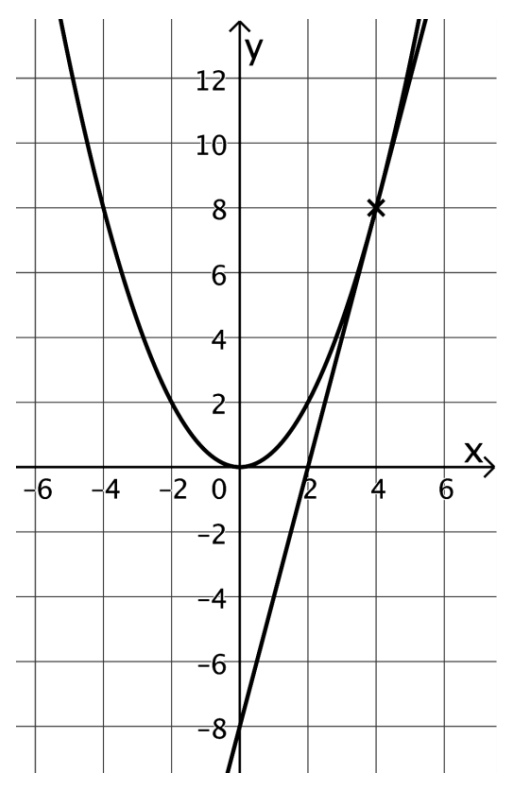
1. Geben Sie anhand der Abbildung eine Gleichung der Tangente $t$ an. [1 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Gleichung der Tangente t
  Tangente mit Steigungsdreieck
  $t: y=m\cdot x+b$
  Der y-Achsenabschnitt $b = - 8$ (Schnitt von $t$ mit der y-Achse) und mit dem eingezeichneten Steigungsdreieck erhält man $m=\dfrac{\Delta y}{\Delta x}=\dfrac{16}{4}=4$ .
  Also ist $t: y=4\cdot x-8$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $t: y=m\cdot x+b$ .
  Lies den y-Achsenabschnitt $b$ ab.
  Zeichne ein passendes Steigungsdreieck ein und bestimme $m$ .
2. Weisen Sie nach, dass für jeden Wert $𝑢 ∈ \R$ die Tangente an den Graphen von $𝑓$ im Punkt $(𝑢 ∣ 𝑓 (𝑢))$ die 𝑦-Achse im Punkt $(0 ∣ - 𝑓 (𝑢))$ schneidet. [4 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Tangente an den Graphen von $f_{a}$ im Punkt $(u ∣ f_{a} (u))$ schneidet die y-Achse im Punkt $(0 ∣ - f_{a} (u))$
  Es ist $f_a(x)=ax^2 \;\Rightarrow\; f_a'(x)=2ax$ und der Punkt ist $(u ∣ f_{a} (u))$ .
  $\Rightarrow\; f_a'(u)=2au=m_T$
  Weiterhin gilt für die Tangente:
  $t: y=m_T\cdot x+b=2au\cdot x+b$
  Setze die Koordinaten von $(u ∣ f_{a} (u))$ in $t: y=2au\cdot x+b$ ein:
  $t: f_a(u)=2au\cdot u+b\;\Rightarrow\;b=f_a(u)-2au^2$
  Mit $f_{a} (u) = a u^{2}$ folgt dann für $b = a u^{2} - 2 a u^{2} = - a u^{2}$
  Damit erhält man für die Tangentengleichung im Punkt $(u ∣ f_{a} (u))$ :
  $\displaystyle t: y=2au\cdot x-au^2$
  Für den Schnittpunkt der Tangente $t$ mit der y-Achse setze $x = 0$ in $t$ ein:
  $t: y=2au\cdot x-au^2$ mit $x = 0$ folgt $y = - a u^{2} = - f_{a} (u)$
  Also ist:
  $\displaystyle S_y(0|-f_a(u))$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Gleichung der Tangente für $f_{a} (x)$ im Punkt $(u ∣ f_{a} (u))$ .
  Setze $x = 0$ in die Tangentengleichung ein, um den Schnittpunkt mit der y-Achse zu bekommen.
8
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe R2
In einem Betrieb werden Geräte hergestellt, von denen jedes mit einer Wahrscheinlichkeit
von $90 %$ fehlerfrei ist. Eine Kontrolle identifiziert ein fehlerfreies Gerät mit einer Wahrscheinlichkeit von $99 %$ . Dagegen wird ein fehlerhaftes Gerät mit einer Wahrscheinlichkeit von $5 %$ ebenfalls als fehlerfrei eingestuft.
1. Zeigen Sie, dass die Wahrscheinlichkeit dafür, dass ein Gerät fehlerfrei ist und
  als fehlerfrei eingestuft wird, $89{,}1 \;\%$ beträgt. [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Zeige, dass die Wahrscheinlichkeit dafür, dass ein Gerät fehlerfrei ist und als fehlerfrei eingestuft wird, $89{,}1 \;\%$ beträgt
  Es ist $p=0{,}9\cdot 0{,}99=0{,}891$
  Die Wahrscheinlichkeit dafür, dass ein Gerät fehlerfrei ist und als fehlerfrei eingestuft wird, beträgt demnach $89{,}1 \;\%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte die Pfadregeln.
2. Formulieren Sie eine Aussage im Sachzusammenhang, die sich in Verbindung
  mit der Gleichung $0,891 + 0,1 \cdot 0,05 = 0,896 0{,}891 + 0{,}1 ⋅ 0{,}05 = 0{,}896$ aus der folgenden Ungleichung ergibt:
  $\displaystyle \sum^{100}_{k=90} \binom{100}{k} \cdot 0{,}896^k⋅ 0{,}104^{100−k} > 0{,}5$ . [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Formuliere eine Aussage im Sachzusammenhang
  $F$ : das Gerät ist fehlerfrei, $\overline{F}$ : das Gerät ist nicht fehlerfrei
  Die Gleichung $0,891 + 0,1 \cdot 0,05 = 0,896 0{,}891 + 0{,}1 ⋅ 0{,}05 = 0{,}896$ ergibt die Wahrscheinlichkeit, dass das Gerät fehlerfrei ist.
  Es ist: $P(F)=0{,}9\cdot 0{,}99+0{,}1\cdot0{,}05=0{,}891 + 0{,}1 ⋅ 0{,}05 = 0{,}896$
  $P(X\geq 90)=\displaystyle \sum^{100}_{k=90} \binom{100}{k} \cdot 0{,}896^k⋅ 0{,}104^{100−k} > 0{,}5$
  Der Term beschreibt die Wahrscheinlichkeit dafür, dass bei der Kontrolle von $100$ Geräten mindestens $90$ als fehlerfrei eingestuft werden, ist größer als $50 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Was beschreibt die Gleichung $0,891 + 0,1 \cdot 0,05 = 0,896 0{,}891 + 0{,}1 ⋅ 0{,}05 = 0{,}896$ ?
  $0,896$ erscheint auch im Term $\displaystyle \sum^{100}_{k=90} \binom{100}{k} \cdot 0{,}896^k⋅ 0{,}104^{100−k} > 0{,}5$
  Was beschreibt dann dieser Term?

Aufgabe R3

Betrachtet wird das Quadrat, das folgende Eigenschaften besitzt:

Das Quadrat liegt in der $x_{1} x_{2}$ -Ebene.
Ein Eckpunkt liegt im Koordinatenursprung.
Der Schnittpunkt der Diagonalen des Quadrats liegt

auf der Geraden g mit $\vec x = \begin{pmatrix}1\\1\\0\end{pmatrix}+\lambda\cdot\begin{pmatrix}2\\3\\0\end{pmatrix}$ , $\lambda \in \mathbb{R}$ ,

und auf der Geraden $h ℎ$ mit $\vec x = \begin{pmatrix}0\\4\\3\end{pmatrix}+\mu\cdot\begin{pmatrix}-1\\0\\1\end{pmatrix}$ , $\mu \in \mathbb{R}$ .

Bestimmen Sie die Koordinaten des Schnittpunkts der Diagonalen und berechnen Sie den Flächeninhalt des Quadrats. [5 BE]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden

Bestimme die Koordinaten des Schnittpunkts der Diagonalen

Berechne den Schnittpunkt $M$ der beiden Geraden.

$g\cap h$ :

$\displaystyle \begin{pmatrix}1\\1\\0\end{pmatrix}+\lambda\cdot\begin{pmatrix}2\\3\\0\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}0\\4\\3\end{pmatrix}+\mu\cdot\begin{pmatrix}-1\\0\\1\end{pmatrix}$	$\displaystyle -\begin{pmatrix}1\\1\\0\end{pmatrix}$
$\displaystyle \lambda\cdot\begin{pmatrix}2\\3\\0\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}-1\\3\\3\end{pmatrix}+\mu\cdot\begin{pmatrix}-1\\0\\1\end{pmatrix}$

Aus Gleichung $\mathrm{(II)}$ folgt: $3\cdot \lambda=3\;\Rightarrow\;$ $\lambda =1$

Aus Gleichung $\mathrm{(III)}$ folgt: $0=3+\mu\;\Rightarrow\;$ $\mu=-3$

Kontrolle in Gleichung $\mathrm{(I)}$ : $2\cdot1=-1+(-3)\cdot (-1)=2\;\checkmark$

Damit folgt für den Vektor $\overrightarrow{OM}=\begin{pmatrix}1\\1\\0\end{pmatrix}+1\cdot\begin{pmatrix}2\\3\\0\end{pmatrix}=\begin{pmatrix}3\\4\\0\end{pmatrix}\;\Rightarrow\;M(3|4|0)$

Berechne den Flächeninhalt des Quadrats

$\Big\vert\overrightarrow{OM}\Big\vert=\sqrt{3^2+4^2}=5$

Die Diagonale des Quadrates ist dann $d=2\cdot 5=10$ und die Seitenlänge $a$ des Quadrates ist $a=\dfrac{d}{\sqrt{2}}$ :

$a=\dfrac{d}{\sqrt{2}}=\dfrac{10}{\sqrt{2}}\;\Rightarrow\;A=a^2=\left(\dfrac{10}{\sqrt{2}}\right)^2=\dfrac{100}{2}=50$

Der Flächeninhalt des Quadrats beträgt $50\;\text{FE}$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \begin{pmatrix}-4\\-t\\3\end{pmatrix}\circ\begin{pmatrix}-6\\-t\\-20\end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Berechne das Skalarprodukt.
$\displaystyle (-4)\cdot (-6)+(-t)\cdot (-t)+3\cdot(-20)$	$=$	$\displaystyle 0$
	↓	Vereinfache.
$\displaystyle 24+t^2-60$	$=$	$\displaystyle 0$	$\displaystyle +60-24$
$\displaystyle t^2$	$=$	$\displaystyle 36$	$\displaystyle \sqrt{}$
$\displaystyle t_{1{,}2}$	$=$	$\displaystyle \pm6$

Pflichtteil

Aufgabe P1

Der Graph von fff ist symmetrisch bezüglich des Koordinatenursprungs

Hast du eine Frage oder Feedback?

Berechne den Inhalt dieser Fläche

Hast du eine Frage oder Feedback?

Aufgabe P2

Die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen roten Ball erhält, ist kleiner als 10 %10\; \%10%

Hast du eine Frage oder Feedback?

Gib dieses Ereignis an

Hast du eine Frage oder Feedback?

Aufgabe P3

Gib die Koordinaten des Punktes GGG an

Hast du eine Frage oder Feedback?

Ermittle die Koordinaten des Punktes H′H'H′

Hast du eine Frage oder Feedback?

Gib einen Eckpunkt des Quaders A′B′C′D′E′F′G′H′A'B'C'D'E'F'G'H'A′B′C′D′E′F′G′H′ an, der nur positive Koordinaten hat

Hast du eine Frage oder Feedback?

Aufgabe Q1

Bestimme grafisch den Wert des Integrals

Hast du eine Frage oder Feedback?

Beschreibe, wie der Graph der in R\RR definierten Funktion uuu mit 𝑢(𝑥)=−𝑓(𝑥)+2𝑢(𝑥) = −𝑓(𝑥) + 2u(x)=−f(x)+2 aus 𝐺𝑓𝐺_𝑓Gf​ erzeugt werden kann

Gib die Koordinaten des Hochpunkts des Graphen von 𝑢𝑢u an

Hast du eine Frage oder Feedback?

Aufgabe Q2

Gib diese Möglichkeiten an

Hast du eine Frage oder Feedback?

Berechne, wie viele Möglichkeiten es dafür gib

Hast du eine Frage oder Feedback?

Aufgabe Q3

Gibt es einen Wert von ttt, für den die Gerade PQtPQ_tPQt​ parallel zur xy-Ebene verläuft

Hast du eine Frage oder Feedback?

Ermittele diejenigen Werte von ttt, für die das Dreieck in QtQ_tQt​ einen rechten Winkel hat

Hast du eine Frage oder Feedback?

Aufgabe R1

Gleichung der Tangente t

Hast du eine Frage oder Feedback?

Tangente an den Graphen von faf_afa​ im Punkt (u∣fa(u))(u|f_a(u))(u∣fa​(u)) schneidet die y-Achse im Punkt (0∣−fa(u))(0|-f_a(u))(0∣−fa​(u))

Hast du eine Frage oder Feedback?

Aufgabe R2

Zeige, dass die Wahrscheinlichkeit dafür, dass ein Gerät fehlerfrei ist und als fehlerfrei eingestuft wird, 89,1 %89{,}1 \;\%89,1% beträgt

Hast du eine Frage oder Feedback?

Formuliere eine Aussage im Sachzusammenhang

Hast du eine Frage oder Feedback?

Aufgabe R3

Bestimme die Koordinaten des Schnittpunkts der Diagonalen

Berechne den Flächeninhalt des Quadrats

Der Graph von $f$ ist symmetrisch bezüglich des Koordinatenursprungs

Die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen roten Ball erhält, ist kleiner als $10 %$

Gib die Koordinaten des Punktes $G$ an

Ermittle die Koordinaten des Punktes $H^{'}$

Gib einen Eckpunkt des Quaders $A^{'} B^{'} C^{'} D^{'} E^{'} F^{'} G^{'} H^{'}$ an, der nur positive Koordinaten hat

Beschreibe, wie der Graph der in $R$ definierten Funktion $u$ mit $𝑢 (𝑥) = - 𝑓 (𝑥) + 2$ aus $𝐺_{𝑓}$ erzeugt werden kann

Gib die Koordinaten des Hochpunkts des Graphen von $𝑢$ an

Gibt es einen Wert von $t$ , für den die Gerade $P Q_{t}$ parallel zur xy-Ebene verläuft

Ermittele diejenigen Werte von $t$ , für die das Dreieck in $Q_{t}$ einen rechten Winkel hat

Tangente an den Graphen von $f_{a}$ im Punkt $(u ∣ f_{a} (u))$ schneidet die y-Achse im Punkt $(0 ∣ - f_{a} (u))$

Zeige, dass die Wahrscheinlichkeit dafür, dass ein Gerät fehlerfrei ist und als fehlerfrei eingestuft wird, $89{,}1 \;\%$ beträgt