Gegeben ist die Funktion $f:x\mapsto {\displaystyle \frac{\pi }{4}}-\arctan \left(\begin{array}{c}{\displaystyle \frac{1-x}{x}}\end{array}\right)f:\; x\backslash mapsto\; \backslash dfrac\{\backslash pi\}\{4\}-\backslash arctan\backslash begin\{pmatrix\}\backslash dfrac\{1-x\}\{x\}\backslash end\{pmatrix\}$mit der Definitionsmenge $D_f={\mathbb{R}}^{+}D\_f=\backslash mathbb\{R\}^+$ .

In der Abbildung ist ein Ausschnitt des Graphen der Funktion $x\mapsto \arctan (x)x\backslash mapsto\; \backslash arctan(x)$ mit $\mathbb{R}\backslash mathbb\{R\}$ als Definitionsmenge zu sehen.

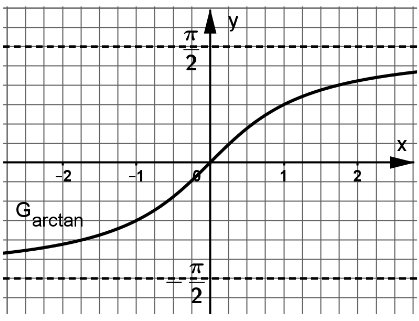
Für die nachfolgenden Teilaufgaben dürfen aus dieser Abbildung evtl. benötigte Funktionswerte entnommen werden.