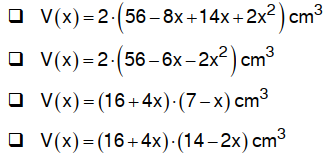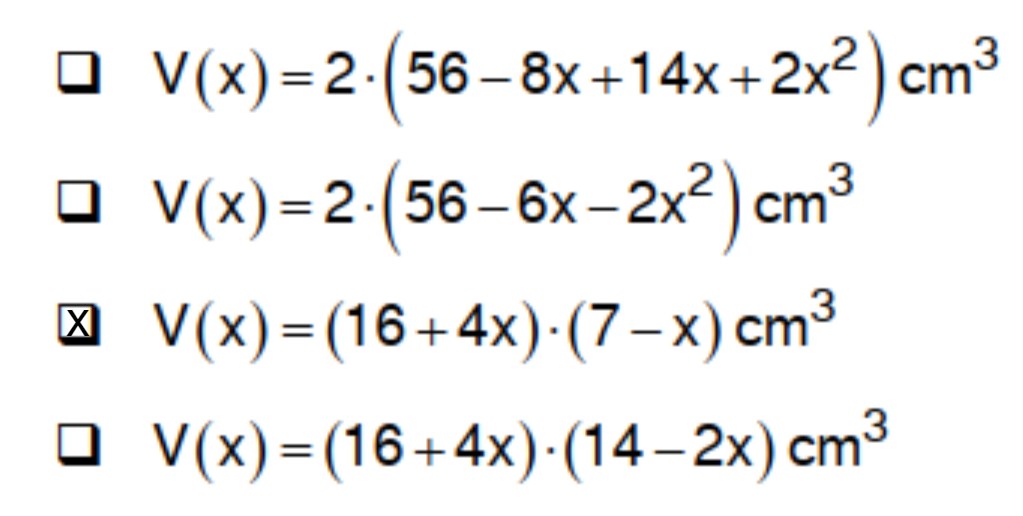Teil A - lernen mit Serlo!

Aufgabe A 2

Die Raute $A B C D$ mit dem Diagonalenschnittpunkt $M$ ist die Grundfläche der Pyramide $A B C D S$ . Das Schrägbild zeigt diese Pyramide mit ihrer Höhe $\overline{MS}$ .

Es gilt: $|\overline{AC}|= 8\;\mathrm{cm}; |\overline{BD}| =12\;\mathrm{cm}; |\overline{MS}| = 7\;\mathrm{cm}.$

In der Zeichnung gilt: $q=\dfrac{1}{2}$ ; $\omega=45^\circ; \overline{AC}$ liegt auf der Schrägbildachse.

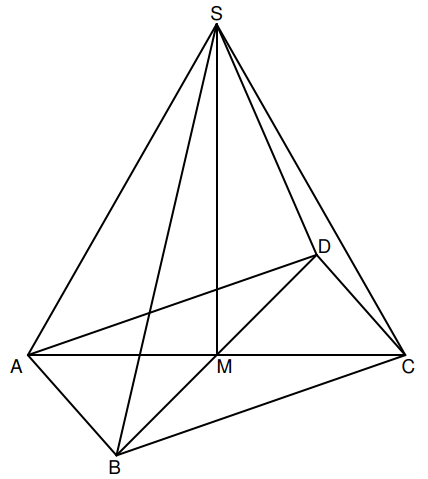
Es entstehen neue Pyramiden $A B C_{n} D S_{n}$ mit den Höhen $\overline{MS_n}$ und den Grundflächen $A B C_{n} D$ , wenn man die Strecke $\overline{AC}$ über $C$ hinaus um $2x\;\mathrm{cm}$ verlängert und gleichzeitig die Strecke $\overline{MS}$ von $S$ aus um $x\;\mathrm{cm}$ verkürzt $(x \in \mathbb{R} ; 0 < x < 7)$ .
Zeichnen Sie für $x = 2$ die Pyramide $A B C_{1} D S_{1}$ in das Schrägbild zur Aufgabenstellung ein. (1,5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Verlängere die Strecke $\overline{AC}$ vom Punkt $C$ aus um $4 \;\mathrm{cm}$ . Du erhältst den Punkt $C_{1}$ .
Verkürze die Strecke $\overline{MS}$ vom Punkt $S$ aus um $2 \;\mathrm{cm}$ . Du erhältst den Punkt $S_{1}$ .
Verbinde alle Punkte zur Pyramide $A B C_{1} D S_{1}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Verlängere die Strecke $\overline{AC}$ vom Punkt $C$ aus um $4 \;\mathrm{cm}$ . Du erhältst den Punkt $C_{1}$ .
Verkürze die Strecke $\overline{MS}$ vom Punkt $S$ aus um $2 \;\mathrm{cm}$ . Du erhältst den Punkt $S_{1}$ .
Verbinde alle Punkte zur Pyramide $A B C_{1} D S_{1}$ .
Für das Volumen $V$ der Pyramiden $A B C_{n} D S_{n}$ in Abhängigkeit von $x$ gilt:
$V(x)= \dfrac{1}{3}\cdot \dfrac{1}{2}\cdot 12\cdot(8+2x)\cdot(7-x)\;\mathrm{cm}^3$ .
Bei welchem der folgenden Terme wurde $V (x)$ richtig umgeformt?
Kreuzen Sie diesen Term an. (1 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Termumformung mit Variablen
Kreuze diesen Term an
Beim 1. Term müsste es in der Klammer $- 2 x^{2}$ heißen.
Beim 2. Term müsste es $+ 6 x$ heißen.
Beim 4. Term wurde die $2$ sowohl in die 1. Klammer als auch in die 2. Klammer multipliziert.
Richtig ist Term 3.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Multipliziere die 2 mit dem 1. Term und vergleiche.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Aufgabe A 2

Hast du eine Frage oder Feedback?

Kreuze diesen Term an

Hast du eine Frage oder Feedback?