Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe A 1
Im folgenden Koordinatensystem ist die Parabel gezeichnet .
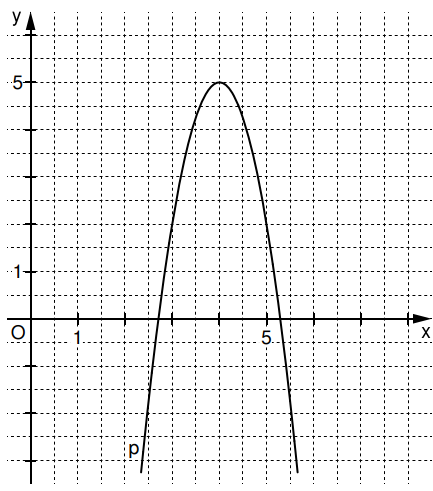
Geben Sie die Gleichung der Parabel in der Scheitelpunktform an. Entnehmen Sie
der Zeichnung die dazu erforderlichen Informationen. (2 P)
Geben Sie die Gleichung einer Geraden an, die keinen gemeinsamen Punkt mit der
Parabel hat. (1 P)
- 2
Aufgabe A 2
Die Raute mit dem Diagonalenschnittpunkt ist die Grundfläche der Pyramide . Das Schrägbild zeigt diese Pyramide mit ihrer Höhe .
Es gilt:
In der Zeichnung gilt: ; liegt auf der Schrägbildachse.
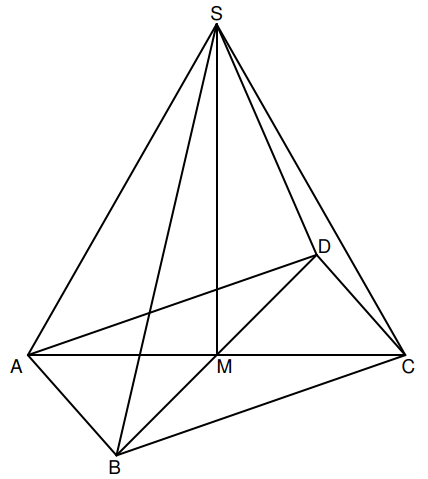
Es entstehen neue Pyramiden mit den Höhen und den Grundflächen , wenn man die Strecke über hinaus um verlängert und gleichzeitig die Strecke von aus um verkürzt .
Zeichnen Sie für die Pyramide in das Schrägbild zur Aufgabenstellung ein. (1,5 P)
Für das Volumen der Pyramiden in Abhängigkeit von gilt:
.
Bei welchem der folgenden Terme wurde richtig umgeformt?
Kreuzen Sie diesen Term an. (1 P)
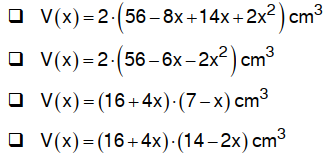
- 3
Aufgabe A 3
Ein Baumarkt bietet zehn gleich große Christbaumkugeln in einer zylinderförmigen Verpackung an.
Ermitteln Sie das ungefähre Volumen der Verpackung in Wirklichkeit. Schätzen Sie die dafür benötigten Größen anhand des Bildes ab. (4 P)

- 4
Aufgabe A 4
Gegeben ist das Dreieck .
Es gilt: .
Zeigen Sie rechnerisch, dass das Dreieck rechtwinklig ist.
Geben Sie an, bei welchem Eckpunkt der rechte Winkel liegt. (2 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?