Teil B: Stochastik
🎓 Prüfungsbereich für Nordrhein-Westfalen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe 1
Ein bekannter Video-Streamingdienst bietet einen kostenpflichtigen Zugang zu Spielfilmen und Serien an. Personen, die davon gegen Zahlung einer monatlichen Gebühr Gebrauch machen, werden im Folgenden als Abonnenten bezeichnet. Sie haben sich entweder für das Spielfilmpaket oder für das Komplettpaket entschieden, das neben den Spielfilmen auch noch Serien enthält.
Unter den Abonnenten sind höchstens Jahre alt. Von diesen haben das Komplettpaket gewählt. Unter denjenigen Abonnenten, die älter sind als Jahre, haben sich für das Komplettpaket entschieden.
Stellen Sie den Sachverhalt in einem beschrifteten Baumdiagramm dar. (3 P)
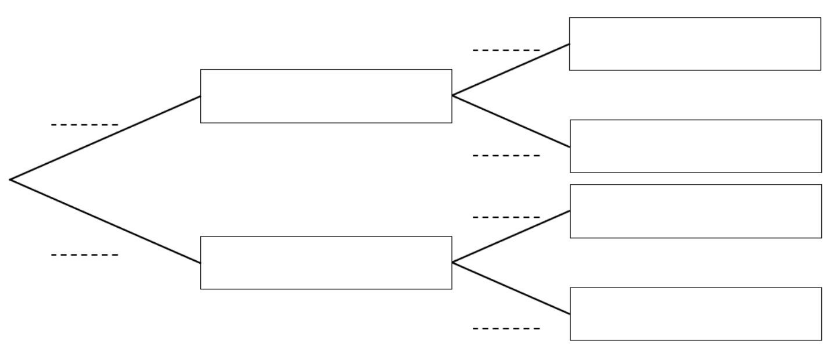
Eine unter allen Abonnenten zufällig ausgewählte Person hat sich für das Komplettpaket entschieden.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass sie höchstens Jahre alt ist. (3 P)
Im Folgenden wird modellhaft davon ausgegangen, dass die Anzahl der höchstens 40-jährigen Abonnenten des Streamingdienstes binomialverteilt mit ist.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass unter zufällig ausgewählten Abonnenten genau höchstens Jahre alt sind. (2 P)
Bestimmen Sie die Anzahl der Abonnenten, die man mindestens zufällig auswählen müsste, damit unter ihnen mit einer Wahrscheinlichkeit von mindestens mehr als Personen älter sind als Jahre. (4 P)
- 2
Aufgabe 2
Nach Aufgabe 1 gilt:
Ein bekannter Video-Streamingdienst bietet einen kostenpflichtigen Zugang zu Spielfilmen und Serien an. Personen, die davon gegen Zahlung einer monatlichen Gebühr Gebrauch machen, werden im Folgenden als Abonnenten bezeichnet. Sie haben sich entweder für das Spielfilmpaket oder für das Komplettpaket entschieden, das neben den Spielfilmen auch noch Serien enthält.
Der Anteil der zufriedenen Abonnenten von derzeit soll gesteigert werden. Dazu wird ein Algorithmus entwickelt, der jedem Abonnenten täglich individuell einen Spielfilm vorschlägt. Als Basis für die Entscheidung über den dauerhaften Einsatz des Algorithmus plant das Management einen Probebetrieb.
Im Anschluss soll mit einer Umfrage unter zufällig ausgewählten Abonnenten untersucht werden, ob der Anteil der zufriedenen Abonnenten durch diese Maßnahme vergrößert wurde.
Von einer Vergrößerung des Anteils zufriedener Abonnenten wird ausgegangen, wenn von den Abonnenten mindestens zufrieden sind.
Die Zufallsgröße : „Anzahl der nach dem Probebetrieb zufriedenen Abonnenten unter den Befragten“ wird durch eine Binomialverteilung mit den Parametern und modelliert.
Ermitteln Sie, mit welcher Wahrscheinlichkeit das Management von einer Vergrößerung des Anteils zufriedener Abonnenten ausgeht, falls der Anteil der zufriedenen Abonnenten unverändert geblieben ist. (2 P)
(i) Ermitteln Sie die Wahrscheinlichkeit dafür, dass das Management davon ausgeht, dass die Maßnahme nicht erfolgreich war, falls der Anteil zufriedener Abonnenten nach dem Probebetrieb auf gestiegen ist. (2 P)
(ii) Die folgende Abbildung zeigt zwei Histogramme von binomialverteilten Zufallsgrößen bzw. mit und bzw. . (2 P)
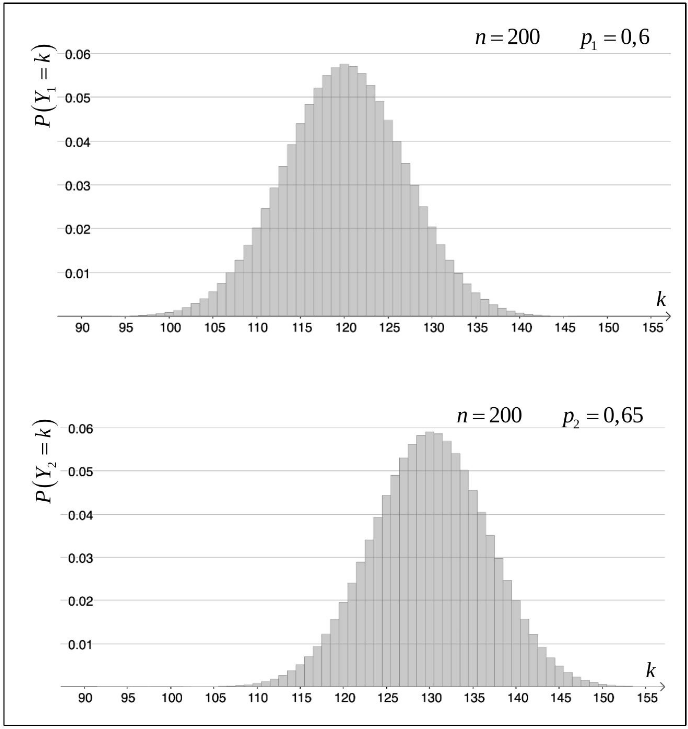
Abbildung
Veranschaulichen Sie die Wahrscheinlichkeiten aus a) und b) (i) in der Abbildung.
(iii) Ein Mitarbeiter des Managements ist der Meinung, dass die Wahrscheinlichkeit für die in b) (i) beschriebene Fehlentscheidung zu hoch ist. Er schlägt vor, die Maßnahme bereits bei mindestens mit dem Angebot zufriedenen Abonnenten als erfolgreich einzustufen.
Beurteilen Sie diesen Vorschlag. (2 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


