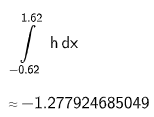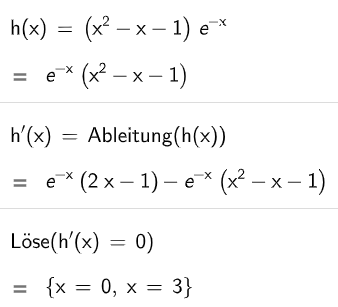B1 - lernen mit Serlo!

Aufgabe 2

Gegeben ist die in definierte Funktion .

Bestimmen Sie die Größe der Fläche, die der Graph von und die -Achse einschließen. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Bestimme die Größe der Fläche, die der Graph von und die -Achse einschließen
Gegeben:
Berechne die Nullstellen :
Verwende Satz vom Nullprodukt:
für alle
Der TR liefert .
Berechne nun das Integral
Die Größe der Fläche, die der Graph von und die -Achse einschließen, beträgt rund .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Nullstellen und .
Dann berechnet man den Flächeninhalt mit .
(i) Zeigen Sie: . (2 P)
(ii) Berechnen Sie die Koordinaten der beiden Extrempunkte des Graphen von sowie den Abstand der Extrempunkte. (2 P + 2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
(i) Zeige:
Wende die Produkt- und Kettenregel an..
(ii) Berechne die Koordinaten der beiden Extrempunkte des Graphen von h sowie den Abstand der Extrempunkte
Notwendige Bedingung für Extremstellen: .
Die Nullstellen sind also .
Laut Aufgabenstellung hat der Graph von nur zwei Extrempunkte.
Da nur zwei Nullstellen besitzt, muss es sich um die Extremstellen handeln.
Gesucht ist also der Abstand der Punkte und .
Es gilt:
Der Abstand der Extrempunkte beträgt rund .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
(i)
Wende die Produkt- und Kettenregel an.
(ii)
Berechne für die Extrema . und
Berechne die Koordinaten der beiden Extrema und .
Der Abstand der Extrempunkte berechnet sich dann mit:.
Die beiden Extrempunkte und des Graphen von bilden zusammen mit den Punkten und ein Rechteck , dessen Seiten parallel zu den Koordinatenachsen verlaufen. Dieses Rechteck wird durch den Graphen der Funktion in zwei Teilstücke zerlegt
(siehe Abbildung 1).
Ermitteln Sie, welchen Anteil an der Fläche des Rechtecks die Fläche des schraffierten Teilstücks einnimmt. (2 P + 2 P + 2 P)
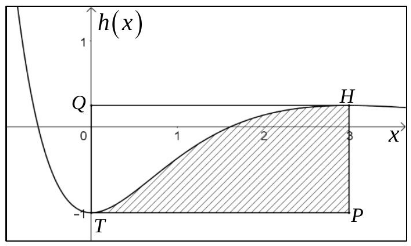
Abbildung 1
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Ermittele, welchen Anteil an der Fläche des Rechtecks die Fläche des schraffierten Teilstücks einnimmt
Gegeben: und .
Der Flächeninhalt des Rechtecks berechnet sich durch:
.
Der Flächeninhalt des Rechtecks beträgt rund .
Schraffiert ist die Fläche zwischen dem Graphen von und der Geraden mit der Gleichung über dem Intervall .
Ihr Inhalt beträgt .
Der Inhalt der schraffierten Fläche beträgt rund .
Damit ergibt sich ein Anteil von , also von ca. .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte die Koordinaten der beiden Extrema und berechne den Flächeninhalt des Rechtecks.
Berechne den Inhalt der schraffierten Fläche mit:
Bilde das Verhältnis .

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 2

Bestimme die Größe der Fläche, die der Graph von und die -Achse einschließen

Hast du eine Frage oder Feedback?

(i) Zeige:

(ii) Berechne die Koordinaten der beiden Extrempunkte des Graphen von h sowie den Abstand der Extrempunkte

Hast du eine Frage oder Feedback?

Ermittele, welchen Anteil an der Fläche des Rechtecks die Fläche des schraffierten Teilstücks einnimmt

Hast du eine Frage oder Feedback?