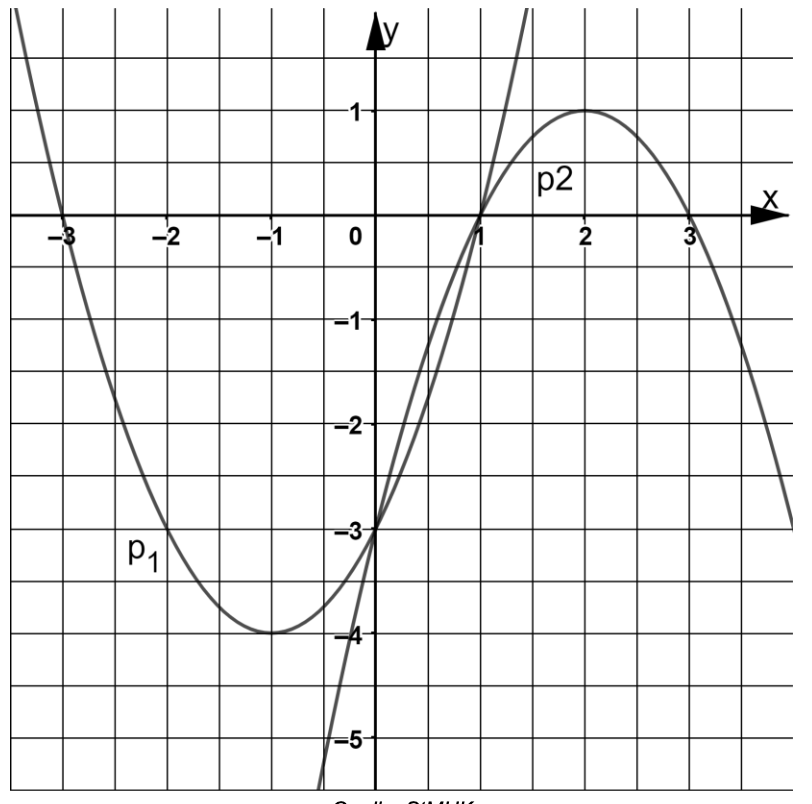
Die nach oben geöffnete Normalparabel verläuft durch die Punkte
und
Berechnen Sie die Funktionsgleichung von in der Normalform.
Die nach unten geöffnete Normalparabel hat den Scheitelpunkt .
Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
Zeichnen Sie die Parabeln und in ein Koordinatensystem mit der
Längeneinheit .
Die Parabel hat die Funktionsgleichung : .
Bestimmen Sie rechnerisch die Koordinaten des Scheitelpunkts .
Der Punkt liegt auf der Parabel .
Berechnen Sie die y-Koordinate des Punkts .
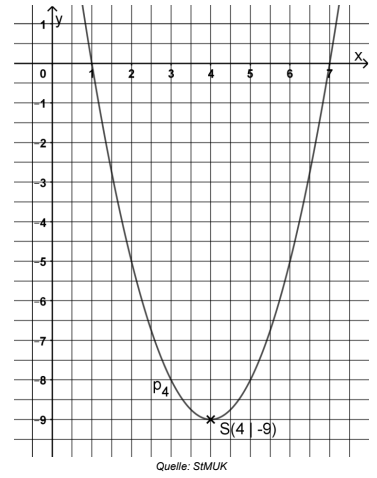
Die folgende Abbildung zeigt die Normalparabel .
Lesen Sie die x-Koordinaten der Nullstellen von aus dem Graphen ab
und überprüfen Sie diese rechnerisch.
In der folgenden Aufgabenstellung ist ein mathematischer Fehler enthalten.
„Gegeben ist die Parabel : y 3. Berechnen Sie die Koordinaten
der zwei Schnittpunkte von mit der y-Achse.“
Ändern Sie die Aufgabenstellung so, dass sie mathematisch korrekt ist.
Notieren Sie diese auf Ihrem Lösungsblatt.
/8
WICHTIG: Damit alle Bilder und Formeln gedruckt werden, scrolle bitte einmal bis zum Ende der Seite BEVOR du diesen Dialog öffnest. Vielen Dank!
🎓 Ui, schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.