In einer Getränkekiste befinden sich ungeordnet Flaschen mit gleicher Form.
Drei Flaschen enthalten Wasser (W), fünf Flaschen Apfelschorle (A) und die
restlichen Holunderschorle (H).
Da die Kiste in einem sehr dunklen Kellerraum steht, sieht man erst nach dem
Verlassen des Raums, welches Getränk man entnommen hat.
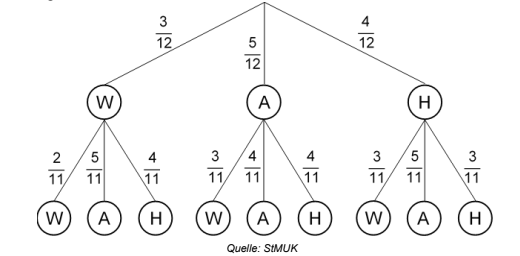
Yannis holt sich zweimal nacheinander je eine Flasche aus der Kiste.
Stellen Sie die möglichen Ergebnisse in einem Baumdiagramm dar.
Beschriften Sie die Äste mit den jeweiligen Wahrscheinlichkeiten.
Berechnen Sie die Wahrscheinlichkeit, dass Yannis beide Male eine Flasche
mit Holunderschorle entnimmt.
Ermitteln Sie rechnerisch die Wahrscheinlichkeit dafür, dass keine der beiden
Flaschen Apfelschorle enthält.
Geben Sie die Anzahl der möglichen Getränkekombinationen aus den zwei
Flaschen an. Die Reihenfolge der Entnahme wird dabei nicht berücksichtigt.
_/4