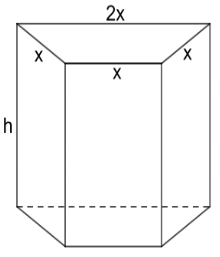
Eine neue Sorte Pralinen soll mit ansprechender Verpackung auf den Markt kommen. Diese hat die nebenstehend abgebildete Form eines geraden Prismas mit trapezförmiger Grundfläche. Das Volumen der Verpackungsschachtel beträgt . Die Maßzahl A der Oberfläche der oben offenen Schachtel in
lässt sich in Abhängigkeit von der Länge in (siehe nebenstehende Abbildung) durch die Gleichung mit
darstellen. Auf die Mitführung der Einheiten kann beiden folgenden Rechnungen verzichtet werden. Runden Sie Ihre Ergebnisse falls nicht anders gefordert auf zwei Nachkommastellen.
In Bild 1 und Bild 2 sind zwei mögliche Verpackungsschachteln mit einem Volumen von nicht maßstäblich dargestellt. Zeigen Sie, dass beide Schachteln ganzzahlig gerundet den gleichen Oberflächeninhalt haben.
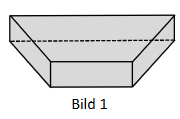
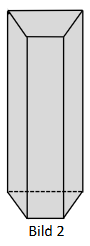
Beide Schachteln verursachen die gleichen Herstellungskosten. Nennen Sie zwei Kriterien, die bei einer Entscheidung für eine der beiden Verpackungsschachteln ausschlaggebend sein können.
(4 BE)
Aus Umweltschutzgründen soll die Verpackung eine möglichst geringe Oberfläche haben. Ermitteln Sie die Länge in so, dass für minimal ist und berechnen Sie die Maßzahl des minimalen Oberflächeninhalts.
mögliches Teilergebnis: (6 BE)
Zeichnen Sie den Graphen der Funktion für in ein geeignetes Koordinatensystem. Kennzeichnen Sie am Graphen die Punkte und . Geben Sie die Koordinaten des absoluten Hochpunktes von an. (6 BE)
Ein Süßwarenhersteller entscheidet sich für eine Schachtel mit bei einem Volumen von . Berechnen Sie die Flächenmaßzahl des trapezförmigen Bodens und die Höhe der zugehörigen Schachtel. (3 BE)


