Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1 und 2.
Das Hotel soll aus drei Gebäuden bestehen, die jeweils die gleiche Form besitzen. Durch den Körper wird Gebäude I modelliert, die Gebäude II und III sind gegenüber Gebäude I jeweils um gedreht (siehe Abbildung 4). Alle drei Gebäude stehen so aneinander, dass sie einen dreieckigen Innenhof bilden. In der Modellierung liegt dieser Innenhof in der -Ebene.
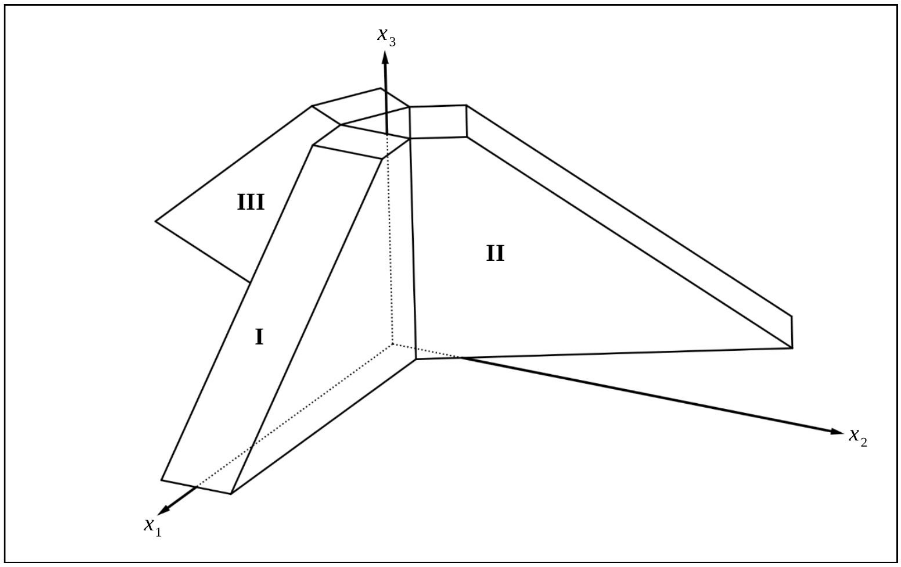
Abbildung 4
Die nebenstehende Abbildung 5 zeigt das Modell des Hotels von oben.
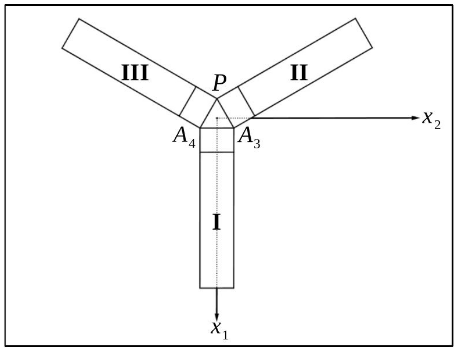
Abbildung 5
Der Innenhof hat die Form eines gleichseitigen Dreiecks.
Ermitteln Sie rechnerisch die Koordinaten des Punktes .
[Zur Kontrolle: (3 P)
Berechnen Sie den Abstand von zum Koordinatenursprung . (2 P)
