Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für die Funktion mit .
Dabei entspricht eine Längeneinheit im Koordinatensystem in der Realität.
Siehe Abbildung 2:
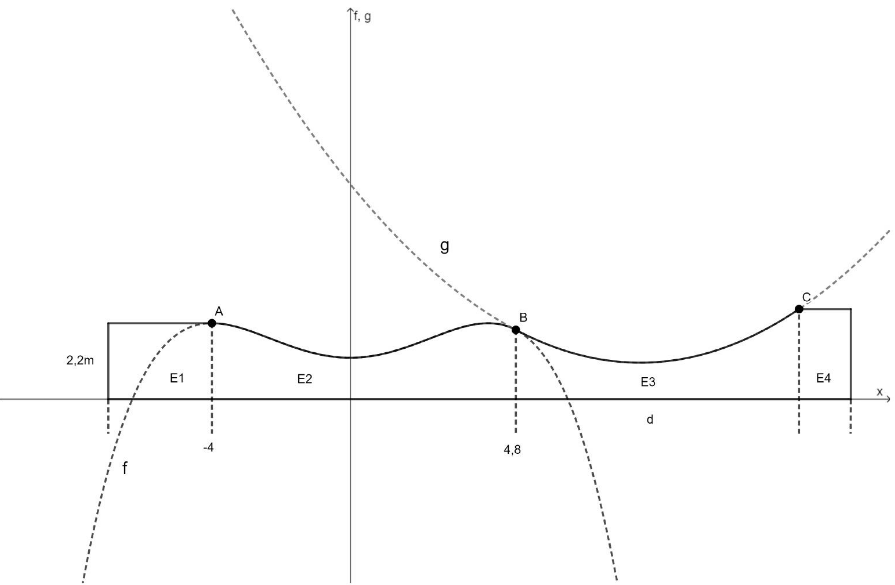
Abbildung 2
Die obere Randlinie von Element E3 soll durch eine ganzrationale Funktion zweiten Grades modelliert werden, deren Graph im Punkt sowohl im Funktionswert als auch in der Steigung mit dem Graphen von übereinstimmt (siehe Abbildung 2). Dabei soll der tiefste Punkt der oberen Randlinie von E3 in horizontaler Entfernung vom Punkt liegen.
Ermitteln Sie eine Gleichung der Funktion . (5 P)
