B3

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
In einem kartesischen Koordinatensystem sind die Punkte $A (0 | 0 | 0), B, C (0 | 100 | 0)$ , $D (0 | 0 | 246), E (48 | 64 | 246)$ und $F (0 | 100 | 246)$ sowie der Punkt $G (0 | 0 | 146)$ gegeben.
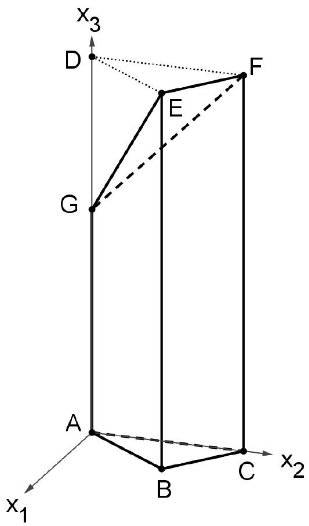
Abbildung
1. Der in der Abbildung dargestellte Körper $A B C D E F$ ist ein dreieckiges Prisma.
  Geben Sie die Koordinaten des Punktes $B$ an. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
  Gib die Koordinaten des Punktes $B$ an
  Der Punkt $B$ liegt in der $x_{1} x_{2}$ -Ebene senkrecht unterhalb von $E (48 | 64 | 246)$ .
  Somit hat $B$ die Koordinaten $B (48 | 64 | 0)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Punkt $B$ liegt in der $x_{1} x_{2}$ -Ebene senkrecht unterhalb von $E (48 | 64 | 246)$ .
2. Für $a \geq 0$ ist der Punkt $G_{a} (0 | 0 | a)$ gegeben.
  Zeigen Sie, dass das Dreieck $G_{a} E F$ für jedes $a \geq 0$ im Punkt $E$ rechtwinklig ist. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Zeige, dass das Dreieck $G_{a} E F$ für jedes $a \geq 0$ im Punkt $E$ rechtwinklig ist
  Berechne die Vektoren $\vec{E G_{a}}$ und $\vec{E F}$ .
  $\vec{E G_{a}} = \vec{O G_{a}} - \vec{O E} = (\begin{array}{c} 0 \\ 0 \\ a \end{array}) - (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) = (\begin{array}{c} - 48 \\ - 64 \\ a - 246 \end{array})$
  $\vec{E F} = \vec{O F} - \vec{O E} = (\begin{array}{c} 0 \\ 100 \\ 246 \end{array}) - (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) = (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array})$
  Damit das Dreieck $G_{a} E F$ für jedes $a \geq 0$ im Punkt $E$ rechtwinklig ist, muss das Skalarprodukt der beiden Vektoren $\vec{E G_{a}}$ und $\vec{E F}$ null ergeben.
  $\vec{E G_{a}} \cdot \vec{E F} = (\begin{array}{c} - 48 \\ - 64 \\ a - 246 \end{array}) \circ (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array}) = 2304 - 2304 + 0 = 0$
  Für jedes $a \geq 0$ ist die Rechtwinkligkeit des Dreiecks $G_{a} E F$ im Punkt $E$ gegeben.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Vektoren $\vec{E G_{a}}$ und $\vec{E F}$ und ihr Skalarprodukt, das gleich null sein muss.
3. Der Punkt $G_{a}$ soll die Strecke $A D$ im Verhältnis $2 : 1$ teilen.
  Geben Sie ein $a \geq 0$ so an, dass $G_{a}$ diese Bedingung erfüllt. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Strecke im Verhältnis teilen
  Gib ein $a \geq 0$ so an, dass $G_{a}$ diese Bedingung erfüllt
  Es ist $g_{A D} : \vec{x} = r \cdot (\begin{array}{c} 0 \\ 0 \\ 246 \end{array})$ .
  Wenn der Punkt $G_{a}$ die Strecke $A D$ im Verhältnis $2 : 1$ teilen soll, dann muss $r = \frac{2}{3}$ sein.
  $G_{a}$ liegt auf $g_{A D}$ $\Rightarrow (\begin{array}{c} 0 \\ 0 \\ a \end{array}) = \frac{2}{3} \cdot (\begin{array}{c} 0 \\ 0 \\ 246 \end{array})$ $\Rightarrow a = \frac{2}{3} \cdot 246 = 164$
  Für $a = 164$ (bzw. $a = 82$ ) teilt $G_{a}$ die Strecke $A D$ im Verhältnis $2 : 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  $G_{a}$ liegt auf $g_{A D}$ .
  Wenn der Punkt $G_{a}$ die Strecke $A D$ im Verhältnis $2 : 1$ teilen soll, dann muss der Parameter der Geraden $g_{A D}$ gleich $\frac{2}{3}$ sein.
4. Für $a = 246$ gilt $G_{a} = D$ .
  Berechnen Sie den Flächeninhalt des Dreiecks $D E F$ und das Volumen des Prismas $A B C D E F$ . (3 P)
  $[$ Zur Kontrolle: $V_{Prisma} = 590400 VE$ . $]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prisma
  Berechne den Flächeninhalt des Dreiecks $D E F$
  Das Dreieck $D E F$ ist rechtwinklig (siehe Aufgabe b) im Punkt $E$ .
  $A_{D E F} = \frac{1}{2} \cdot | \vec{E D} | \cdot | \vec{E F} |$
  $\vec{E D} = (\begin{array}{c} - 48 \\ - 64 \\ 0 \end{array}) \Rightarrow | \vec{E D} | = \sqrt{(- 48)^{2} + (- 64)^{2}} = 80$
  $\vec{E F} = (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array}) \Rightarrow | \vec{E F} | = \sqrt{(- 48)^{2} + 36^{2}} = 60$
  $A_{D E F} = \frac{1}{2} \cdot 80 \cdot 60 = 2400$
  Der Flächeninhalt des Dreiecks $D E F$ beträgt $2400 FE .$
  Berechne das Volumen des Prismas $A B C D E F$
  Es gilt: $V_{Prisma} = A_{DEF} \cdot h_{Prisma}$
  Dabei ist $A_{D E F} = 2400$ und $h_{Prisma}$ ist gleich der $x_{3}$ -Koordinate von $D$ .
  $\Rightarrow V_{Prisma} = 2400 \cdot 246 = 590400$
  Das Volumen des Prismas $A B C D E F$ beträgt $590400 VE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Das Dreieck $D E F$ ist rechtwinklig (siehe Aufgabe b) im Punkt $E$ . $A_{D E F} = \frac{1}{2} \cdot | \vec{E D} | \cdot | \vec{E F} |$
  Teil 2
  Es gilt: $V_{Prisma} = A_{DEF} \cdot h_{Prisma}$
  $A_{D E F}$ wurde im Teil 1 berechnet und $h_{Prisma}$ ist gleich der $x_{3}$ -Koordinate von $D$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
In einem kartesischen Koordinatensystem sind die Punkte $A (0 | 0 | 0), B, C (0 | 100 | 0)$ , $D (0 | 0 | 246), E (48 | 64 | 246)$ und $F (0 | 100 | 246)$ sowie der Punkt $G (0 | 0 | 146)$ gegeben.
Weiterhin bekannt ist der Flächeninhalt des Dreiecks $A_{D E F} = 2400 F E$ und das Volumen des Prismas aus Aufgabe 1: $V_{Prisma} = 590400 V E .$
Abbildung
Ein Architekturbüro plant den Neubau eines Wolkenkratzers, der durch den Körper mit den Eckpunkten $A B C G E F$ modelliert wird, wobei im gewählten Koordinatensystem eine Längeneinheit einem Meter in der Realität entspricht.
1. Die Länge der Kante $A G$ musste wegen der geltenden Bauvorschriften im Vergleich zur Länge der Kante $A D$ um $100 m$ auf $146 m$ reduziert werden. Durch diese Reduzierung wird von dem Prisma $A B C D E F$ eine Pyramide mit der Grundfläche $D E F$ abgeschnitten.
  Berechnen Sie, um wie viel Prozent sich das Volumen des Gebäudes $A B C G E F$ im Vergleich zum Volumen des Prismas $A B C D E F$ verkleinert hat. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Berechne, um wie viel Prozent sich das Volumen des Gebäudes $A B C G E F$ im Vergleich zum Volumen des Prismas $A B C D E F$ verkleinert hat
  Bekannt sind $A_{D E F} = 2400 F E$ und $V_{Prisma} = 590400 V E .$
  Das Pyramidenvolumen berechnet sich mit $V_{Pyramide} = \frac{1}{3} \cdot A_{D E F} \cdot h$ .
  Dabei ist $h = 246 - 146 = 100 m$ .
  $\Rightarrow V_{Pyramide} = \frac{1}{3} \cdot 2400 \cdot 100 = 80000 V E$
  Mit $\frac{80000}{590400} \approx 0,1355$ hat sich das Volumen um ca. $13,55 %$ verkleinert.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Das Pyramidenvolumen berechnet sich mit $V_{Pyramide} = \frac{1}{3} \cdot A_{D E F} \cdot h$ .
  Bilde das Verhältnis $\frac{V_{Pyramide}}{V_{Prisma}}$ .
2. Berechnen Sie den Winkel zwischen den Kanten $F C$ und $F G$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
  Berechne den Winkel zwischen den Kanten $F C$ und $F G$
  Berechne die Vektoren $\vec{F C}$ und $\vec{F G}$ und ihre Beträge:
  $\vec{F C} = \vec{O C} - \vec{O F} = (\begin{array}{c} 0 \\ 100 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 100 \\ 246 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ - 246 \end{array})$
  $| \vec{F C} | = 246$
  $\vec{F G} = \vec{O G} - \vec{O F} = (\begin{array}{c} 0 \\ 0 \\ 146 \end{array}) - (\begin{array}{c} 0 \\ 100 \\ 246 \end{array}) = (\begin{array}{c} 0 \\ - 100 \\ - 100 \end{array})$
  $| \vec{F G} | = \sqrt{0 + (- 100)^{2} + (- 100)^{2}} = \sqrt{20000} = 100 \cdot \sqrt{2}$
  Für den Winkel $α$ zwischen den Kanten $F C$ und $F G$ gilt dann:
  $\cos α = \frac{\vec{F C} \circ \vec{F G}}{| \vec{F C} | \cdot | \vec{F G} |} = \frac{(\begin{array}{c} 0 \\ 0 \\ - 246 \end{array}) \circ (\begin{array}{c} 0 \\ - 100 \\ - 100 \end{array})}{246 \cdot 100 \cdot \sqrt{2}} = \frac{(- 246) \cdot (- 100)}{246 \cdot 100 \cdot \sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$ .
  Dann ist $α = c o s^{- 1} (\frac{\sqrt{2}}{2}) = 45^{\circ}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Vektoren $\vec{F C}$ und $\vec{F G}$ und ihre Beträge.
  Dann ist $\cos α = \frac{\vec{F C} \circ \vec{F G}}{| \vec{F C} | \cdot | \vec{F G} |} .$
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
In einem kartesischen Koordinatensystem sind die Punkte $A (0 | 0 | 0), B, C (0 | 100 | 0)$ , $D (0 | 0 | 246), E (48 | 64 | 246)$ und $F (0 | 100 | 246)$ sowie der Punkt $G (0 | 0 | 146)$ gegeben.
Abbildung
1. Zeigen Sie, dass $E_{Dach} : \vec{x} = (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) + s \cdot (\begin{array}{c} - 48 \\ - 64 \\ - 100 \end{array}) + t \cdot (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array}), s \in ℝ, t \in ℝ$ , eine Parametergleichung der Ebene ist, in der die Dachfläche $G E F$ liegt. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene aus drei Punkten
  Zeige, dass
  $E_{Dach} : \vec{x} = (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) + s \cdot (\begin{array}{c} - 48 \\ - 64 \\ - 100 \end{array}) + t \cdot (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array}), s \in ℝ, t \in ℝ$ ,
  eine Parametergleichung der Ebene ist, in der die Dachfläche $G E F$ liegt
  Berechne die Vektoren $\vec{E G}$ und $\vec{E F}$ .
  $\vec{E G} = \vec{O G} - \vec{O E} = (\begin{array}{c} 0 \\ 0 \\ 146 \end{array}) - (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) = (\begin{array}{c} - 48 \\ - 64 \\ - 100 \end{array})$
  $\vec{E F} = \vec{O F} - \vec{O E} = (\begin{array}{c} 0 \\ 100 \\ 246 \end{array}) - (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) = (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array})$
  Dann folgt für die Parametergleichung der Ebene $E_{Dach}$ :
  $E_{Dach} : \vec{x} = \vec{O E} + s \cdot \vec{E G} + t \cdot \vec{E F} = (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) + s \cdot (\begin{array}{c} - 48 \\ - 64 \\ - 100 \end{array}) + t \cdot (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array})$
  (mit $s \in ℝ, t \in ℝ$ )
  Somit ist die gegebene Ebene eine Parametergleichung der Ebene $E_{Dach}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Vektoren $\vec{E G}$ und $\vec{E F}$ .
  Berechne dann die Ebenengleichung $E_{Dach} : \vec{x} = \vec{O E} + s \cdot \vec{E G} + t \cdot \vec{E F}$ und vergleiche mit der gegebenen Ebenengleichung.
2. Alle Punkte der dreieckigen Dachfläche $G E F$ sind gegeben durch
  $\vec{x} = (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) + s \cdot (\begin{array}{c} - 48 \\ - 64 \\ - 100 \end{array}) + t \cdot (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array}), s \geq 0, t \geq 0, s + t \leq 1$
  Ein Lufttaxi soll den Wolkenkratzer mit einem anderen Wolkenkratzer verbinden. Im letzten Teil des Fluges soll es auf einer Strecke fliegen, die vereinfachend als Teil der Geraden $g : \vec{x} = (\begin{array}{c} 4 \\ 10 \\ 200 \end{array}) + k \cdot (\begin{array}{c} 3 \\ 7 \\ - 1 \end{array}), k \in ℝ$ , modelliert werden kann.
  Zeigen Sie rechnerisch, dass die Gerade $g$ einen Punkt der dreieckigen Dachfläche $G E F$ enthält. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
  Zeige rechnerisch, dass die Gerade $g$ einen Punkt der dreieckigen Dachfläche $G E F$ enthält
  Gegeben sind $E_{GEF} : \vec{x} = (\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) + s \cdot (\begin{array}{c} - 48 \\ - 64 \\ - 100 \end{array}) + t \cdot (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array}), s \geq 0, t \geq 0, s + t \leq 1$ und $g : \vec{x} = (\begin{array}{c} 4 \\ 10 \\ 200 \end{array}) + k \cdot (\begin{array}{c} 3 \\ 7 \\ - 1 \end{array}), k \in ℝ$
  Schneide $g$ mit $E$ :
  $(\begin{array}{c} 48 \\ 64 \\ 246 \end{array}) + s \cdot (\begin{array}{c} - 48 \\ - 64 \\ - 100 \end{array}) + t \cdot (\begin{array}{c} - 48 \\ 36 \\ 0 \end{array}) = (\begin{array}{c} 4 \\ 10 \\ 200 \end{array}) + k \cdot (\begin{array}{c} 3 \\ 7 \\ - 1 \end{array})$
  Man erhält das Gleichungssystem:
  $| \begin{array}{l} - 48 s - 48 t - 3 k = - 44 \\ - 64 s + 36 t - 7 k = - 54 \\ - 100 s + 0 t + k = - 46 \end{array} |$ .
  Der TR liefert als Lösung $s = \frac{1}{2}, t = \frac{1}{6}$ und $k = 4$ .
  Wenn der Schnittpunkt im Dreieck $G E F$ liegen soll, dann müssen die Bedingungen $s \geq 0, t \geq 0, s + t \leq 1$ erfüllt sein.
  $s = \frac{1}{2} \geq 0, t = \frac{1}{6} \geq 0$ und $\frac{1}{2} + \frac{1}{6} = \frac{2}{3} \leq 1 ✓$
  Alle 3 Bedingungen sind erfüllt. Somit enthält die Gerade $g$ einen Punkt der dreieckigen Dachfläche $G E F$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Schneide $g$ mit $E$ $\Rightarrow s, t, k .$
  Wenn der Schnittpunkt im Dreieck $G E F$ liegen soll, dann müssen die Bedingungen $s \geq 0, t \geq 0, s + t \leq 1$ erfüllt sein.
  Überprüfe die Bedingungen mit Deinen Lösungen.
3. Ein weiteres Lufttaxi erreicht im Punkt $Q (16 | 38 | 196)$ die Dachfläche, nachdem es $45 m$ auf einer Strecke in Richtung $\vec{v} = (\begin{array}{c} 10 \\ 11 \\ - 2 \end{array})$ geflogen ist.
  Ermitteln Sie den Startpunkt dieser geradlinigen Flugstrecke. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
  Ermittele den Startpunkt dieser geradlinigen Flugstrecke
  Gegeben: Das Lufttaxi fliegt $45 m$ auf einer Strecke in Richtung $\vec{v} = (\begin{array}{c} 10 \\ 11 \\ - 2 \end{array})$ und erreicht im Punkt $Q (16 | 38 | 196)$ die Dachfläche.
  Berechne $| \vec{v} |$ :
  $| \vec{v} | = \sqrt{10^{2} + 11^{2} + (- 2)^{2}} = \sqrt{225} = 15$
  Da das Lufttaxi $45 m$ geflogen ist, muss vom Punkt $P$ aus dreimal der Vektor $\vec{v}$ addiert werden, um zum Punkt $Q (16 | 38 | 196)$ zu gelangen.
  $\Rightarrow \vec{O P} + 3 \cdot (\begin{array}{c} 10 \\ 11 \\ - 2 \end{array}) = (\begin{array}{c} 16 \\ 38 \\ 196 \end{array}) \Rightarrow \vec{O P} = (\begin{array}{c} 16 \\ 38 \\ 196 \end{array}) - 3 \cdot (\begin{array}{c} 10 \\ 11 \\ - 2 \end{array}) = (\begin{array}{c} - 14 \\ 5 \\ 202 \end{array})$
  Der Startpunkt dieser geradlinigen Flugstrecke hat die Koordinaten $P (- 14 | 5 | 202)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $| \vec{v} |$ .
  Da das Lufttaxi $45 m$ geflogen ist, muss vom Punkt $P$ aus dreimal der Vektor $\vec{v}$ addiert werden, um zum Punkt $Q (16 | 38 | 196)$ zu gelangen.
  Löse die Gleichung nach $P$ auf.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B3

Aufgabe 1

Gib die Koordinaten des Punktes B an

Hast du eine Frage oder Feedback?

Zeige, dass das Dreieck GaEF für jedes a≥0 im Punkt E rechtwinklig ist

Hast du eine Frage oder Feedback?

Gib ein a≥0 so an, dass Ga diese Bedingung erfüllt

Hast du eine Frage oder Feedback?

Berechne den Flächeninhalt des Dreiecks DEF

Berechne das Volumen des Prismas ABCDEF

Hast du eine Frage oder Feedback?

Aufgabe 2

Berechne, um wie viel Prozent sich das Volumen des Gebäudes ABCGEF im Vergleich zum Volumen des Prismas ABCDEF verkleinert hat

Hast du eine Frage oder Feedback?

Berechne den Winkel zwischen den Kanten FC und FG

Hast du eine Frage oder Feedback?

Aufgabe 3

Zeige, dass

eine Parametergleichung der Ebene ist, in der die Dachfläche GEF liegt

Hast du eine Frage oder Feedback?

Zeige rechnerisch, dass die Gerade g einen Punkt der dreieckigen Dachfläche GEF enthält

Hast du eine Frage oder Feedback?

Ermittele den Startpunkt dieser geradlinigen Flugstrecke

Hast du eine Frage oder Feedback?

Gib die Koordinaten des Punktes $B$ an

Zeige, dass das Dreieck $G_{a} E F$ für jedes $a \geq 0$ im Punkt $E$ rechtwinklig ist

Gib ein $a \geq 0$ so an, dass $G_{a}$ diese Bedingung erfüllt

Berechne den Flächeninhalt des Dreiecks $D E F$

Berechne das Volumen des Prismas $A B C D E F$

Berechne, um wie viel Prozent sich das Volumen des Gebäudes $A B C G E F$ im Vergleich zum Volumen des Prismas $A B C D E F$ verkleinert hat

Berechne den Winkel zwischen den Kanten $F C$ und $F G$

eine Parametergleichung der Ebene ist, in der die Dachfläche $G E F$ liegt

Zeige rechnerisch, dass die Gerade $g$ einen Punkt der dreieckigen Dachfläche $G E F$ enthält