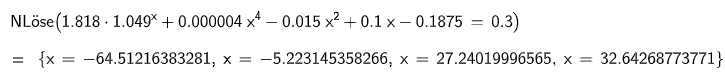B2 - lernen mit Serlo!

Aufgabe 3

Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.

Abbildung 2 zeigt schematisch die Profillinie des Längsschnittes einer Skipiste in einer Skihalle. Die Piste ist in Querrichtung nicht geneigt und durchgehend $30\mathrm{~m}$ breit.

Die Profilinie wird für $0 \leq x \leq 41{,}5$ modellhaft durch den Graphen der in $\mathbb{R}$ definierten Funktion $p$ mit $p(x)=-0{,}000004 x^{4}+0{,}015 x^{2}-0{,}1 x+0{,}1875$ dargestellt.

Im verwendeten Koordinatensystem beschreibt die $x$ -Achse die Horizontale; eine Längeneinheit im Koordinatensystem entspricht $10\mathrm{~m}$ in der Realität.

Bestimmen Sie die größte Neigung der Piste gegenüber der Horizontalen in Prozent.
(3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
Bestimme die größte Neigung der Piste gegenüber der Horizontalen in Prozent
Gegeben ist $p(x)=-0{,}000004 x^{4}+0{,}015 x^{2}-0{,}1 x+0{,}1875$ .
Gesucht ist das Maximum der 1. Ableitung von $p (x)$ :
Berechne $p^{'} (x)$ , $p^{''} (x)$ und $p^{'''} (x)$ :
$p'(x)=-0{,}000016x^{3}+0{,}03 x-0{,}1$
$p''(x)=-0{,}000048x^{2}+0{,}03$
$p^{'''} (x) = - 0,000096 x$
Die notwendige Bedingung für ein Extremum ist $p^{''} (x) = 0$ .
$0=-0{,}000048x^{2}+0{,}03\;\Rightarrow\;x_{1{,}2}=\pm\sqrt{\dfrac{0{,}03}{0{,}000048}}=\pm\sqrt{625}=\pm 25$ .
Wegen $0 \leq x \leq 41{,}5$ ist $x = 25$ .
Nachweis, dass es sich um ein Maximum handelt:
$p'''(25)=-0{,}000096\cdot 25=-0{,}0024<0\;\Rightarrow\;$ Maximum
Die größte Neigung der Piste:
Für $x = 25$ liegt ein Maximum vor.
Berechne $p'(25)=-0{,}000016\cdot 25^{3}+0{,}03 \cdot 25-0{,}1=0{,}4=40\;\%$ .
Für $x = 25$ hat die Piste die größte Neigung gegenüber der Horizontalen mit $40 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Gesucht ist das Maximum der 1. Ableitung von $p (x)$ .
Berechne $p^{'} (x)$ , $p^{''} (x)$ und $p^{'''} (x)$ .
Die notwendige Bedingung für ein Extremum ist $p''(x)=0\;\Rightarrow\;x_1$
Berechne $p^{'} (x_{1})$ und gib den Wert in $%$ an.
Über der Piste verläuft in deren Längsrichtung ein Seil. Die beiden Enden des Seils werden im Modell durch $A(5 \mid 2{,}31)$ und $B(37 \mid 10{,}68)$ dargestellt; der Verlauf des Seils kann mithilfe einer in $\mathbb{R}$ definierten Funktion $h$ mit $h(x)=b \cdot c^{x}, b>0, c>0$ beschrieben werden.
Bestimmen Sie die Werte von $b$ und $c$ .
$[$ Zur Kontrolle: $b \approx 1{,}818, c \approx 1{,}049$ $]$ (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Bestimme die Werte von $b$ und $c$
Gegeben sind Funktion $h$ mit $h(x)=b \cdot c^{x}, b>0, c>0$ und die Punkte $A(5 \mid 2{,}31)$ und $B(37 \mid 10{,}68)$ .
Setze die Koordinaten von $A$ in $h$ ein:
$2{,}31=b \cdot c^{5}\;\Rightarrow\;b=\dfrac{2{,}31}{c^{5}}$
Setze $b$ und die Koordinaten von $B$ in $h$ ein:
$10{,}68=\dfrac{2{,}31}{c^{5}}\cdot c^{37}=2{,}31\cdot c^{32}\;\Rightarrow\;c^{32}=\dfrac{10{,}68}{2{,}31}\;\Rightarrow\;c=\sqrt[32]{\dfrac{10{,}68}{2{,}31}}\approx1{,}049$
Dann erhält man für $b=\dfrac{2{,}31}{1{,}049^5}\approx1{,}818$ . (Das ist die Musterlösung, gerundet erhält man $b\approx1{,}819$ .)
Die Werte von $b$ und $c$ sind $b\approx1{,}818$ und $c\approx1{,}049$ .
Dann ist $h(x)=1{,}818\cdot 1{,}049^x$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze die Koordinaten von $A$ in $h$ ein und löse nach $b$ auf.
Setze $b$ und die Koordinaten von $B$ in $h$ ein und berechne $c$ .
Mit dem berechneten $c$ kann $b$ berechnet werden.
Untersuchen Sie, in welchen Bereichen der vertikale Abstand des Seils zur Piste mindestens $3\mathrm{~m}$ beträgt.
Ermitteln Sie die Höhendifferenz, um die die beiden Enden des Seils gemeinsam mindestens angehoben werden müssten, damit das Seil an jeder Stelle von der Piste einen vertikalen Abstand von mindestens $3\mathrm{~m}$ hat. (7 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Untersuche, in welchen Bereichen der vertikale Abstand des Seils zur Piste mindestens 3 m beträgt
Es sind $h(x)=1{,}818\cdot 1{,}049^x$ und $p(x)=-0{,}000004 x^{4}+0{,}015 x^{2}-0{,}1 x+0{,}1875$ .
Weiterhin gilt: Eine Längeneinheit im Koordinatensystem entspricht $10\mathrm{~m}$ in der Realität.
Betrachte die Differenz der beiden Funktionsgleichungen:
$d (x) = h (x) - p (x)$
$d(x)=1{,}818\cdot 1{,}049^x-(-0{,}000004 x^{4}+0{,}015 x^{2}-0{,}1 x+0{,}1875)$
$d(x)=1{,}818\cdot 1{,}049^x+0{,}000004 x^{4}-0{,}015 x^{2}+0{,}1 x-0{,}1875$
Der vertikale Abstand des Seils zur Piste soll mindestens $3\mathrm{~m}$ betragen.
An den Randstellen des Seils, bei $x = 5$ und $x = 37$ beträgt der vertikale Abstand zur Piste $d(5)\approx2{,}24925...$ (etwa $22{,}5\mathrm{~m}$ ) und $d(37)\approx1{,}14754...$ (etwa $11{,}5\mathrm{~m}$ ).
Die Stellen, an denen der Abstand $3\mathrm{~m}$ beträgt, findet man mit der Gleichung $d (x) = 0,3$ .
Löse die Gleichung:
Für $5\leq x\leq 37$ erhält man die beiden Lösungen $x_1\approx27{,}24$ und $x_2\approx32{,}64$ .
Vom Beginn des Seils bis $x_1\approx27{,}24$ und von $x_2\approx32{,}64$ bis $x = 37$ beträgt der vertikale Abstand des Seils zur Piste mindestens $3\mathrm{~m}$ .
Ermittle die Höhendifferenz, um die die beiden Enden des Seils gemeinsam mindestens angehoben werden müssten, damit das Seil an jeder Stelle von der Piste einen vertikalen Abstand von mindestens $3\mathrm{~m}$ hat
Finde graphisch das absolute Minimum der Funktion $d (x)$ im Bereich $27{,}24\leq x\leq 32{,}64$ .
Du erhältst die Minimalstelle bei $x\approx30{,}08821487$ und den y-Wert $y\approx 0{,}1882497763$ .
Der Tiefpunkt hat die gerundeten Koordinaten $TP(30{,}09\mid 0{,}19)$ .
$y = 0,19$ entspricht einem Abstand von $1{,}9\mathrm{~m}$ .
Um einen Abstand von mindestens $3 \mathrm{~m}$ zu haben, muss das Seil um $3 \mathrm{~m}-1{,}9 \mathrm{~m}=1{,}1 \mathrm{~m}$ angehoben werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Betrachte die Differenz der beiden Funktionsgleichungen $d (x) = h (x) - p (x)$ .
Der vertikale Abstand des Seils zur Piste soll mindestens 3 m betragen.
$\Rightarrow\; d(x)=0{,}3$ : Löse die Gleichung mit dem CAS.
Die gesuchten Lösungen $x_{1}$ und $x_{2}$ liegen im Bereich $5\leq x\leq 37$ .
Teil 2
Finde graphisch das absolute Minimum der Funktion $d (x)$ im Bereich $x_1\leq x\leq x_2$ .
Der Tiefpunkt hat die gerundeten Koordinaten $TP(x_m\mid y_m)$ .
Beachte, $y_m\cdot 10$ ist der Abstand in Metern.
Um einen Abstand von mindestens $3 \mathrm{~m}$ zu haben, muss das Seil um $3 -y_m\cdot 10 =z$ Meter angehoben werden.
Abbildung 3 zeigt grau markiert die Schneeauflage im unteren Bereich der Piste; dazu wurde Abbildung 2 in Richtung der $y$ -Achse stärker vergrößert als in Richtung der $x$ -Achse. Der Untergrund, auf dem der Schnee aufgebracht ist, wird für $0 \leq x \leq 5$ durch die $x$ -Achse dargestellt. Für den übrigen Teil der Piste soll davon ausgegangen werden, dass die in vertikaler Richtung gemessene Schneehöhe $60\mathrm{~cm}$ beträgt.
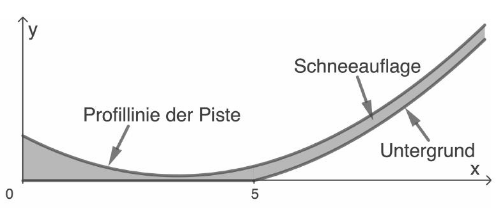
Abbildung 3
Bestimmen Sie das Volumen der Schneeauflage der gesamten Piste. (5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Bestimme das Volumen der Schneeauflage der gesamten Piste
Bekannt ist, dass die in vertikaler Richtung gemessene Schneehöhe $60\mathrm{~cm}$ beträgt, d.h. $60\mathrm{~cm}=0{,}6\mathrm{~m}$ und wegen des Faktors $10$ muss mit $0,06$ gerechnet werden.
Weiterhin gilt: Die Piste ist in Querrichtung nicht geneigt und durchgehend $30\mathrm{~m}$ breit $\;\Rightarrow\; \text{Breite}=30\mathrm{~m}$ .
Berechne zunächst die grau unterlegte Fläche.
Diese Fläche kann in zwei Teile zerlegt werden.
$A=A_1+A_2=\displaystyle\int_0^5p(x)\; \mathrm{d}x+\displaystyle\int_5^{41{,}5}\left(p(x)-(p(x)-0{,}06)\right)\; \mathrm{d}x$
Man erhält folgendes Ergebnis:
Die Fläche ist: $A=A_1+A_2=\dfrac{31}{100}+\dfrac{219}{100}=\dfrac{250}{100}$ , d.h. der Flächeninhalt der Fläche $A$ beträgt $\dfrac{250}{100}\mathrm{~FE}$ . Da $1\mathrm{~FE}$ gleich $100\mathrm{~m}^2$ entspricht, ist die gesuchte Fläche $250\mathrm{~m}^2$ groß.
Dann ist das Volumen der Schneeauflage der gesamten Piste:
$V=\text{Fläche}\cdot \text{Breite}=250\cdot 30=7500$ .
Das Volumen der Schneeauflage der gesamten Piste beträgt $7500\mathrm{~m}^3$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Beachte, die in vertikaler Richtung gemessene Schneehöhe beträgt $60\mathrm{~cm}$ , d.h. $60\mathrm{~cm}=0{,}6\mathrm{~m}$ und wegen des Faktors $10$ muss mit $0,06$ gerechnet werden.
Berechne die grau unterlegte Fläche. Diese Fläche kann in zwei Teile zerlegt werden.
$A=A_1+A_2=\displaystyle\int_0^{x_1}p(x)\; \mathrm{d}x+\displaystyle\int_{x_1}^{x_2}\left(p(x)-(p(x)-0{,}06)\right)\; \mathrm{d}x$
Beachte, $1\mathrm{~FE}$ entspricht $100\mathrm{~m}^2$ .
Das Volumen der Schneeauflage der gesamten Piste ist dann: $V=\text{Fläche}\cdot \text{Breite}=(A\cdot 100)\cdot 30$ .