Pflichtteil A2

🎓 Prüfungsbereich für Baden-Württemberg

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Die Abbildung zeigt eine Bilderfolge aus Streichhölzern.
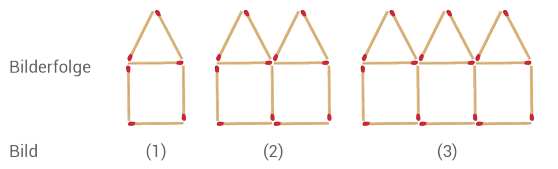
Bestimme die Anzahl der Streichhölzer im 7. Bild.
Thorben hat den Term $6+5\cdot x$ aufgestellt, um die Anzahl der Streichhölzer im $x$ -ten Bild zu bestimmen.
Stimmt Thorbens Term?
Begründe deine Entscheidung.
[ 2 Pkt. ]
2
Diese Perlenketten liegen in einem Behälter und werden blind gezogen.
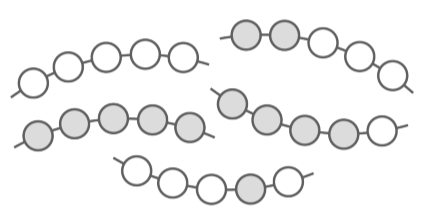
Bestimme die prozentuale Wahrscheinlichkeit, sodass die gezogene Perlenkette beim einmaligen Ziehen ...
(1) graue und weiße Perlen enthält.
(2) mindestens eine und maximal drei weiße Perlen enthält.
Es wird zweimal ohne Zurücklegen gezogen.
Berechne die Wahrscheinlichkeit, dass Perlenketten mit insgesamt genau 3 grauen Kugeln gezogen werden.
[ 3 Pkt. ]
3
Gegeben ist das lineare Gleichungssystem:
(I) $\quad-x+3y=3$
(II) $y = - 2 x + 1$
Beim Berechnen des $x$ -Wertes des linearen Gleichungssystems wurden Fehler gemacht.
Markiere die Fehler und beschreibe, was falsch gemacht wurde.
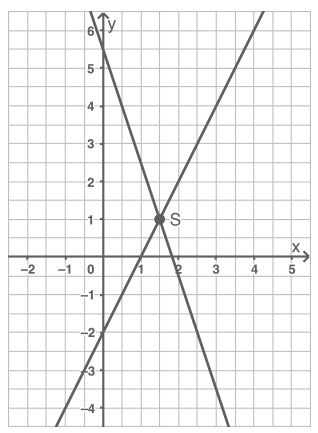
Gegeben ist folgendes Gleichungssystem:
(I) $6 x + 2 y = 11$
(II) $y = 2 x - 2$
Löse das Gleichungssystem zeichnerisch und gib die Lösung an.
4
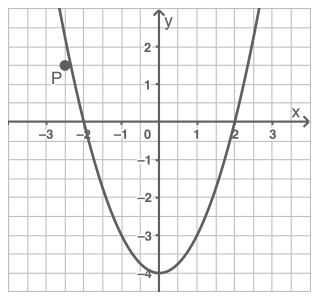
Eine Normalparabel $p_{1}$ hat den Scheitelpunkt $S(0 \mid-4)$ .
Überprüfe, ob der Punkt $P(-2{,}5 \mid 1{,}5)$ auf der Parabel $p_{1}$ liegt.
Thilo behauptet: „Die Parabel $p_{2}$ mit der Funktionsgleichung $y=-\dfrac{1}{10} x^{2}-2$ hat keine Schnittpunkte mit der $x$ -Achse". Hat er Recht?
Begründe deine Entscheidung durch Argumentation.
[2 Pkt]
5
Führe folgende Anweisungen durch:
Zeichne die Punkte $A (6 ∣ 0)$ , $B (6 ∣ 6)$ und $C (- 3 ∣ 3)$ in ein Koordinatensystem (1 LE = 1 cm).
Verbinde die Punkte zu einem Dreieck und gib die besondere Art des Dreiecks an.
Zeichne alle Mittelsenkrechten ein.
Gib den Schnittpunkt $S$ der Mittelsenkrechten an.
[ 3 Pkt. ]
6
Das Säulendiagramm zeigt die Tageshöchsttemperaturen $\left({ }^{\circ} \mathrm{C}\right)$ einer Woche.
(Skizze nicht maßstabsgetreu)
Welche ganzzahligen Temperaturwerte sind für Mittwoch möglich, wenn der fehlende Wert weder das Minimum noch das Maximum ist?
Begründe deine Entscheidung.
In den USA werden Temperaturen in Fahrenheit $\left({ }^{\circ} \mathrm{F}\right)$ angegeben.
Es gilt: $\quad \boxed{ { }^{\circ} \mathrm{F}={ }^{\circ} \mathrm{C}\cdot 1{,}8+32 }$
Berechne die Temperatur in ${ }^{\circ} \mathrm{C}$ , wenn es in New York $59^{\circ} \mathrm{F}$ hat.
[2 Pkt]
7
Im Rechteck $A B C D$ ist das Trapez $A B E F$ eingezeichnet.
Es gilt:
$\def\arraystretch{1.25} \begin{aligned} \overline{A B} & =50 \mathrm{~cm} \\ \overline{B C} & =30 \mathrm{~cm} \\ \overline{B E} & =33{,}5 \mathrm{~cm} \\ \overline{C E} & =15 \mathrm{~cm} \\ \alpha & =75^{\circ} \end{aligned}$
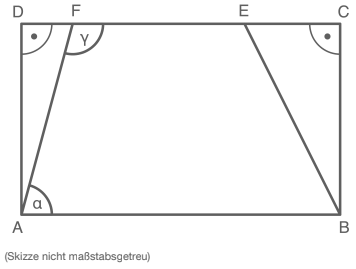
Zeige, dass der Winkel $\gamma=105^{\circ}$ beträgt.
Berechne den Umfang des Trapezes.
[3 Pkt]
8
Im Rechteck $A B C D$ ist das Trapez $A B E F$ eingezeichnet.
Es gilt:
$\overline{AB}=50\cm$
$\overline{BC}=30\cm$
$\overline{BE}=33{,}5\cm$
$\overline{CE}=15\cm$
$\alpha=75°$
Zeige, dass der Winkel $\gamma=105°$ beträgt.
Berechne den Umfang des Trapezes.
[ 3 Pkt. ]
9
1. Kim legt $800\ €$ für 3 Jahre zu einem Zinssatz von $2,5 %$ bei ihrer Bank an (Zinsen werden mitverzinst).
  Mit welchen Termen kann das Endkapital nach 3 Jahren berechnet werden?
  Kreuze an.
  $800\cdot1{,}025\cdot1{,}025\cdot1{,}025$
  $800\cdot075^3$
  $800\cdot2{,}5\%\cdot2{,}5\%\cdot2{,}5\%$
  $800\cdot1{,}025^3$
2. Elif legt bei ihrer Bank $600\;€$ für 4 Jahre an (Zinsen werden mitverzinst).
  Berechne, wieviel Geld Elif nach Ablauf der 4 Jahre erhält.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?