Teil 1: ohne Hilfsmittel – Analysis

1
Gegeben ist die Funktion $f : x \mapsto \frac{2 x}{4 - x^{2}}$ mit der Definitionsmenge $D_{f} =] - 2; 2 [$ .
Ihr Graph in einem kartesischen Koordinatensystem wird mit $G_{f}$ bezeichnet.
1. Geben Sie die Gleichungen aller Asymptoten von $G_{f}$ und die Nullstelle von $f$ an.
  (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Asymptote
  Gib die Gleichungen aller Asymptoten von $G_{f}$ und die Nullstelle von $f$ an
  Asymptoten:
  Verhalten von $f$ am linken Definitionsrand:
  $\lim_{x \to - 2^{+}} \frac{\overset{\to - 4}{\overset{⏞}{2 x}}}{\underset{\to 0}{\underset{⏟}{4 - x^{2}}}} = - \infty$
  Verhalten von $f$ am rechten Definitionsrand:
  $\lim_{x \to 2^{-}} \frac{\overset{\to 4}{\overset{⏞}{2 x}}}{\underset{\to 0}{\underset{⏟}{4 - x^{2}}}} = \infty$
  $\Rightarrow$ Es gibt zwei senkrechte Asymptoten bei $x = - 2$ und $x = 2$ .
  Nullstelle:
  $f (x) = 0 \Rightarrow x = 0$ . Die Nullstelle von $f$ ist $x = 0$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Betrachte das Verhalten von $f$ am linken und am rechten Definitionsrand.
  Teil 2
  Berechne $f (x) = 0$ .
2. Weisen Sie nach, dass die Funktion $f$ in ihrer Definitionsmenge $D_{f}$ umkehrbar ist, und ermitteln Sie die Definitionsmenge der Umkehrfunktion von $f$ . (6 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Umkehrfunktion
  Weise nach, dass die Funktion $f$ in ihrer Definitionsmenge $D_{f}$ umkehrbar ist
  Berechne die Ableitung von $f (x)$ mithilfe der Quotientenregel:
  $f^{'} (x)$ $=$ $\frac{(4 - x^{2}) \cdot 2 - 2 x \cdot (- 2 x)}{(4 - x^{2})^{2}}$
  ↓
  Fasse zusammen.
  $=$ $\frac{8 - 2 x^{2} + 4 x^{2}}{(4 - x^{2})^{2}}$
  $=$ $\frac{2 x^{2} + 8}{(4 - x^{2})^{2}}$
  $f^{'} (x) = \frac{Z (x)}{N (x)}$
  Für alle $x \in D_{f}$ gilt: $Z (x) > 0$ und $N (x) > 0 \Rightarrow f^{'} (x) > 0$
  $\Rightarrow$ $f^{'} (x)$ ist streng monoton steigend $\Rightarrow$ es existiert eine Umkehrfunktion.
  Ermittle die Definitionsmenge der Umkehrfunktion von $f$
  Gegeben ist die Definitionsmenge $D_{f} =] - 2; 2 [$ . Betrachte das Verhalten von $f$ an den Definitionsrändern.
  Verhalten von $f$ am linken Definitionsrand:
  $\lim_{x \to - 2^{+}} \frac{\overset{\to - 4}{\overset{⏞}{2 x}}}{\underset{\to 0}{\underset{⏟}{4 - x^{2}}}} = - \infty$
  Verhalten von $f$ am rechten Definitionsrand:
  $\lim_{x \to 2^{-}} \frac{\overset{\to 4}{\overset{⏞}{2 x}}}{\underset{\to 0}{\underset{⏟}{4 - x^{2}}}} = \infty$
  $\Rightarrow W_{f} =] - \infty; + \infty [\Rightarrow D_{f^{- 1}} =] - \infty; + \infty [$
  Die Definitionsmenge der Umkehrfunktion von $f$ ist $D_{f^{- 1}} =] - \infty; + \infty [$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Berechne die Ableitung von $f (x)$ mithilfe der Quotientenregel und prüfe, ob $f^{'} (x) > 0$ oder ob $f^{'} (x) < 0$ für alle $x \in D_{f}$ ist.
  Teil 2
  Ermittle $W_{f}$ . Dann ist $D_{f^{- 1}} = W_{f}$ .
3. Der Graph von $f$ und die zur x-Achse senkrechte Gerade bei $x = 1$ schließen zusammen mit der x-Achse im I. Quadranten ein Flächenstück ein.
  Berechnen Sie die exakte Maßzahl des Flächeninhalts dieses Flächenstücks. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Berechne die exakte Maßzahl des Flächeninhalts dieses Flächenstücks
  Nach Aufgabe a) ist die Nullstelle $x = 0$ .
  Berechne das Integral $\int_{0}^{1} \frac{2 x}{4 - x^{2}} d x$ .
  Eine Stammfunktion von $f$ ist $F (x) = - \ln | 4 - x^{2} | + C$ .
  Dann folgt:
  $\int_{0}^{1} \frac{2 x}{4 - x^{2}} d x = F (1) - F (0) = - \ln | 4 - 1^{2} | - (- \ln | 4 - 0^{2} |) = - \ln 3 + \ln 4 = \ln \frac{4}{3}$
  Die exakte Maßzahl des Flächeninhalts dieses Flächenstücks beträgt $\ln \frac{4}{3} FE$ .
  Graphische Darstellung:
  Die Abbildung ist in der Aufgabenstellung nicht verlangt worden. Sie dient nur der Veranschaulichung. Hinweis: $\ln \frac{4}{3} \approx 0,2877$
  Flächenberechnung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Nach Aufgabe a) ist die Nullstelle $x = 0$ .
  Berechne das Integral $\int_{0}^{1} \frac{2 x}{4 - x^{2}} d x$ . Ermittle dazu eine Stammfunktion.
4. Gegeben ist nun die Funktion $g : x \mapsto \ln (f (x))$ mit der maximalen Definitionsmenge $D_{g} \subset D_{f}$ . Ermitteln Sie die Definitionsmenge $D_{g}$ und die exakte Nullstelle von $g$ .
  (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen
  Ermittle die Definitionsmenge $D_{g}$
  Es ist $g (x) = \ln (\frac{2 x}{4 - x^{2}})$ mit der maximalen Definitionsmenge $D_{g} \subset D_{f}$ .
  Das Argument vom $\ln$ muss größer null sein $\Rightarrow x > 0 \Rightarrow D_{g} =] 0; 2 [$ .
  Ermittle die exakte Nullstelle von $g$
  Es gilt: $\ln (1) = 0 \Rightarrow 1 = \frac{2 x}{4 - x^{2}}$
  Löse die Gleichung nach $x$ auf.
  $1$ $=$ $\frac{2 x}{4 - x^{2}}$ $\cdot (4 - x^{2})$
  ↓
  Löse nach $x$ auf.
  $4 - x^{2}$ $=$ $2 x$ $+ x^{2} - 4$
  $0$ $=$ $x^{2} + 2 x - 4$
  Du hast eine quadratische Gleichung erhalten. Diese kannst du mit der Mitternachtsformel (abc-Formel) oder pq-Formel lösen. Hier erfolgt die Lösung mit der pq-Formel.
  $x_{1,2}$ $=$ $- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
  ↓
  Setze $p = 2$ und $q = - 4$ ein.
  $=$ $- \frac{2}{2} \pm \sqrt{{(\frac{2}{2})}^{2} - (- 4)}$
  $=$ $- 1 \pm \sqrt{1 + 4}$
  $=$ $- 1 \pm \sqrt{5}$
  Die Lösung $x_{1} = - 1 - \sqrt{5}$ entfällt, da $x_{1} \notin D_{g}$ .
  Die exakte Nullstelle von $g$ ist also $x = - 1 + \sqrt{5}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Das Argument vom $\ln$ muss größer null sein. Was folgt daraus?
  Teil 2
  Es gilt: $\ln (1) = 0$ . Löse die entsprechende Gleichung nach $x$ auf.
2
Die nachfolgende Abbildung zeigt einen Ausschnitt des Graphen $G_{h}$ einer in $ℝ$ stetigen Funktion $h$ . Die x-Achse ist Asymptote von $G_{h}$ . Außerdem gilt: $h (x) \geq 0$ für $x \in ℝ$ .
$G_{h}$
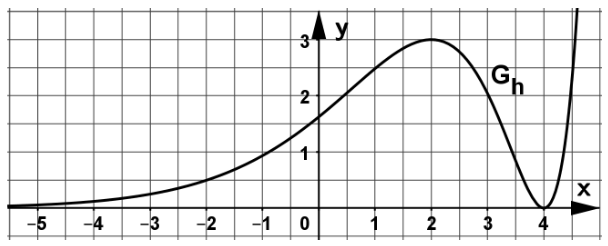
Zudem ist die Funktion $H : x \mapsto \int_{2}^{x} h (t) d t$ mit der Definitionsmenge $D_{H} = ℝ$ gegeben.
Entscheiden Sie für die beiden folgenden Aussagen jeweils, ob die Aussage wahr oder falsch ist, und begründen Sie Ihre Entscheidung.
A: „Der Graph von $H$ besitzt bei $x = 4$ einen Extrempunkt.“
B: „Der Graph von $H$ hat bei $x = 1$ eine Tangente mit einem positiven y-Achsenabschnitt.“
(5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
A: „Der Graph von $H$ besitzt bei $x = 4$ einen Extrempunkt.“
Verwende die NEW-Regel. An der Stelle, an der die Funktion $h$ einen Extrempunkt hat, hat die Stammfunktion einen Wendepunkt.
Damit ist die Aussage $A$ falsch.
B: „Der Graph von $H$ hat bei $x = 1$ eine Tangente mit einem positiven y-Achsenabschnitt.“
$H (1) = \int_{2}^{1} h (t) d t < 0$ , da die obere Grenze kleiner als die untere Grenze ist.
Demnach verläuft $H (x)$ für $0 \leq x < 2$ im $4$ . Quadranten.
Weiterhin gilt: $H^{'} (1) = h (1) > 0$ (siehe $G_{h}$ ).
Der Punkt $P (1 | H (1))$ liegt im $4$ . Quadranten. Die Tangente im Punkt $P (1 | H (1))$ hat eine positive Steigung und der Schnittpunkt mit der y-Achse liegt demnach im negativen
y-Bereich.
Die Aussage $B$ ist falsch.
$A$ : Verwende die NEW-Regel.
$B$ : $H (1) = \int_{2}^{1} h (t) d t < 0$ , da die obere Grenze kleiner als die untere Grenze ist. Demnach verläuft $H (x)$ für $0 \leq x < 2$ im $4$ . Quadranten. Weiterhin ist $H^{'} (1) = h (1) > 0.$ Was folgt dann für die Tangente im Punkt $P (1 | H (1))$ ?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$f^{'} (x)$	$=$	$\frac{(4 - x^{2}) \cdot 2 - 2 x \cdot (- 2 x)}{(4 - x^{2})^{2}}$
	↓	Fasse zusammen.
	$=$	$\frac{8 - 2 x^{2} + 4 x^{2}}{(4 - x^{2})^{2}}$
	$=$	$\frac{2 x^{2} + 8}{(4 - x^{2})^{2}}$

$1$	$=$	$\frac{2 x}{4 - x^{2}}$	$\cdot (4 - x^{2})$
	↓	Löse nach $x$ auf.
$4 - x^{2}$	$=$	$2 x$	$+ x^{2} - 4$
$0$	$=$	$x^{2} + 2 x - 4$

$x_{1,2}$	$=$	$- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
	↓	Setze $p = 2$ und $q = - 4$ ein.
	$=$	$- \frac{2}{2} \pm \sqrt{{(\frac{2}{2})}^{2} - (- 4)}$
	$=$	$- 1 \pm \sqrt{1 + 4}$
	$=$	$- 1 \pm \sqrt{5}$

Teil 1: ohne Hilfsmittel – Analysis

Gib die Gleichungen aller Asymptoten von Gf und die Nullstelle von f an

Hast du eine Frage oder Feedback?

Weise nach, dass die Funktion f in ihrer Definitionsmenge Df umkehrbar ist

Ermittle die Definitionsmenge der Umkehrfunktion von f

Hast du eine Frage oder Feedback?

Berechne die exakte Maßzahl des Flächeninhalts dieses Flächenstücks

Hast du eine Frage oder Feedback?

Ermittle die Definitionsmenge Dg

Ermittle die exakte Nullstelle von g

Hast du eine Frage oder Feedback?

A: „Der Graph von H besitzt bei x=4 einen Extrempunkt.“

B: „Der Graph von H hat bei x=1 eine Tangente mit einem positiven y-Achsenabschnitt.“

Gib die Gleichungen aller Asymptoten von $G_{f}$ und die Nullstelle von $f$ an

Weise nach, dass die Funktion $f$ in ihrer Definitionsmenge $D_{f}$ umkehrbar ist

Ermittle die Definitionsmenge der Umkehrfunktion von $f$

Ermittle die Definitionsmenge $D_{g}$

Ermittle die exakte Nullstelle von $g$

A: „Der Graph von $H$ besitzt bei $x = 4$ einen Extrempunkt.“

B: „Der Graph von $H$ hat bei $x = 1$ eine Tangente mit einem positiven y-Achsenabschnitt.“