Der Punkt $\text{A}(-4|-1)$ liegt auf der Parabel ${\mathrm{p}}_1$ mit der Funktionsgleichung $\mathrm{y}={\mathrm{x}}^2+\mathrm{b}\mathrm{x}+7$. Die Gerade $\text{g}$ schneidet die Parabel ${\mathrm{p}}_1$ im Punkt $\text{A}$ und im Scheitelpunkt ${\mathrm{S}}_1$.

• Berechne die Funktionsgleichungen der Parabel ${\mathrm{p}}_1$ und der Geraden $\text{g}$.

Durch Spiegelung des Scheitelpunkts ${\mathrm{S}}_1$ an der $\text{y}$-Achse entsteht der Punkt ${\mathrm{S}}_2.$${\mathrm{S}}_2$ist der Scheitelpunkt einer nach oben geöffneten verschobenen Normalparabel ${\mathrm{p}}_2$.

• Gib die Funktionsgleichung von ${\mathrm{p}}_2$ in der Form $\mathrm{y}={\mathrm{x}}^2+\mathrm{b}\mathrm{x}+\mathrm{c}$ an.

Der Schnittpunkt der Geraden $\text{g}$ mit der $\text{y}$-Achse ist der Scheitelpunkt ${\mathrm{S}}_3$ der Parabel ${\mathrm{p}}_3$. Die Parabel ${\mathrm{p}}_3$ der Form $\mathrm{y}=\mathrm{a}{\mathrm{x}}^2+\mathrm{c}$ geht außerdem durch die Scheitelpunkte ${\mathrm{S}}_1$ und ${\mathrm{S}}_2$.

• Berechne die Funktionsgleichung der Parabel ${\mathrm{p}}_3$.

(5 P)

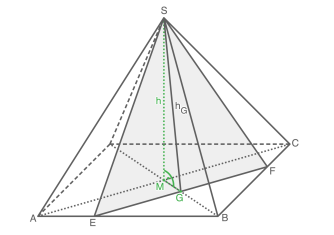
In einer quadratischen Pyramide liegt das gleichschenklige Dreieck $\text{EFS}$.

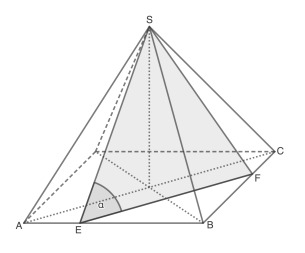
Es gilt:

$\overline{\mathrm{A}\mathrm{B}}=\overline{\mathrm{E}\mathrm{F}}=\mathrm{12,6}\text{ cm}$ $\mathrm{\alpha }=\mathrm{72,0}°$ $\overline{\mathrm{E}\mathrm{F}}\Vert \overline{\mathrm{A}\mathrm{C}}$

• Berechne den Flächeninhalt des Dreiecks $\text{EFS}.$

• Berechne das Volumen der quadratischen Pyramide.

(5 P)