Dieser Inhalt wurde gelöscht.

Prüfungsteil 1 2025

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Schreibe als ganze Zahl:
$0,6 \cdot 10^{4}$ = _______
$\sqrt{49}$ = _______
$(- 2)^{3}$ = _______

$0,6 \cdot 10^{4} = 0,6 \cdot 10000 = 6000$
$\sqrt{49} = 7$
$(- 2)^{3} = (- 2) \cdot (- 2) \cdot (- 2) = 4 \cdot (- 2) = - 8$
2
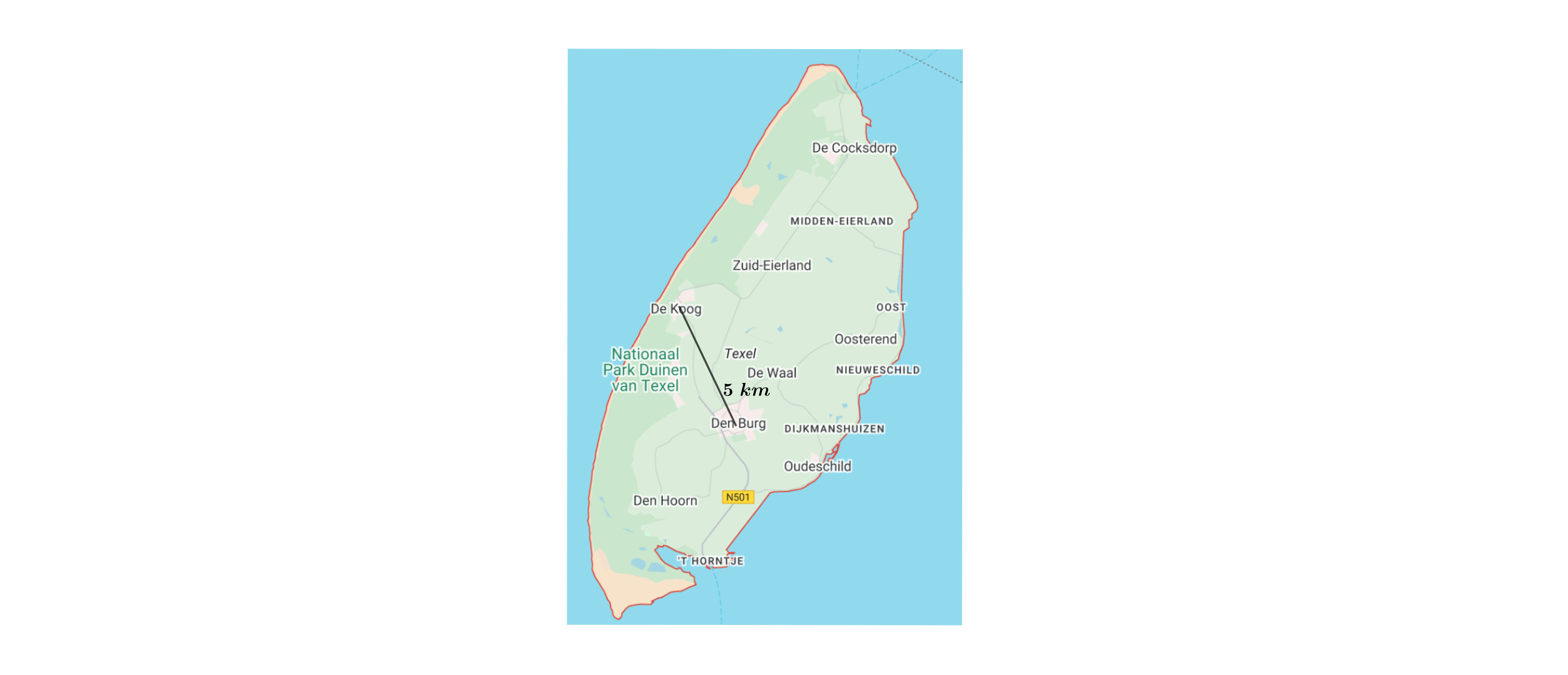
Auf der Insel Texel in den Niederlanden sind die Orte Den Burg und De Koog ungefähr $5 km$ voneinander entfernt (Abbildung rechts).
Schätze ab, wie lang die Insel von ihrem nördlichsten bis zu ihrem südlichsten Punkt ist und beschreibe, wie du vorgegangen bist.
3
1. Berechne den Flächeninhalt der äußeren, schraffierten Fläche für
  $𝑎 = 20 cm, 𝑏 = 8 cm$ und $c = 2 cm$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
  $A_{R e c h t e c k} = l \cdot b$
  Die schraffierte Fläche besteht aus 4 Rechtecken. Zwei davon sind jeweils gleich.
  $A_{s c h r a f f i e r t e F l \ddot{a} c h e} =$ $2 \cdot a \cdot c + 2 \cdot b \cdot c$
  $A_{s c h r a f f i e r t e F l \ddot{a} c h e} = 2 \cdot 20 \cdot 2 + 2 \cdot 8 \cdot 2 = 80 + 32 = 112$
  Die schraffieret Fläche ist $112 {cm}^{2}$ groß.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Gib einen allgemeinen Term zur Berechnung des Flächeninhaltes der inneren, weißen Fläche an. Nutze die Variablen $𝑎$ , $𝑏$ und $𝑐$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
  $A_{R e c h t e c k} = l \cdot b$
  $l = a - 2 \cdot c$
  $A_{R e c h t e c k} = (a - 2 \cdot c) \cdot b$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Im Koordinatensystem ist der Graph der Funktion $𝑓$ mit $𝑓 (𝑥) = 1,5 \cdot 𝑥 - 1$ dargestellt
1. Bestätige rechnerisch, dass der Punkt $𝑃 (4 | 5)$ auf der Geraden von $𝑓$ liegt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
  Setze die Koordinaten des Punktes $P$ in die Funktionsgleichung ein.
  $P (4 | 5)$
  $f (x) = 1,5 \cdot x - 1$
  $f (4) = 1,5 \cdot 4 - 1 = 6 - 1 = 5 ✓$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ergänze die Gerade $𝑔 (𝑥) = 0,5 𝑥 + 3$ im Koordinatensystem.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
In einem Behälter befinden sich 3 weiße und 2 schwarze Kugeln. Es wird ohne hinzusehen gezogen.
1. Begründe, dass die Wahrscheinlichkeit, bei einmaligem Ziehen eine schwarze Kugel zu ziehen, $p = \frac{2}{5}$ beträgt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Anzahl Kugeln gesamt: 5
  Anzahl schwarze Kugeln: 2
  Wahrscheinlichkeit bei einmaligem Ziehen eine schwarze Kugel zu ziehen: $p = \frac{2}{5}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechne die Wahrscheinlichkeit, bei zweimaligem Ziehen ohne Zurücklegen zwei weiße Kugeln zu ziehen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Anzahl Kugeln gesamt: 5
  Anzahl weiße Kugeln: 3
  Wahrscheinlichkeit beim 1. Zug eine weiße Kugel zu ziehen: $p = \frac{3}{5}$ .
  Wahrscheinlichkeit beim 2. Zug eine weiße Kugel zu ziehen, wenn beim 1. Zug bereits eine weiße Kugel gezogen wurde: $p = \frac{2}{4}$ .
  Wahrscheinlichkeit bei zweimaligem Ziehen ohne Zurücklegen zwei weiße Kugeln zu ziehen: $p = \frac{3}{5} \cdot \frac{2}{4} = \frac{6}{20} = \frac{3}{10}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Prüfungsteil 1 2025

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?