1 Übersicht
Inhalte des Kurses
Du weißt jetzt bereits, dass Prozentangaben Verhältnisse beschreiben können. Hier lernst du, wie man mit ihnen rechnet. Es werden wichtige Begriffe wie Grundwert, Prozentwert und Prozentsatz eingeführt. Außerdem lernst du, wie man diese mit dem Dreisatz oder einer Formel berechnet.
Vorkenntnisse
Der Kurs Einführung des Prozentzeichens und seiner Umrechnung gilt als Grundvoraussetzung für diesen Kurs.
Prozente als Darstellung von Brüchen und Dezimalzahlen.
Dir sollte klar sein, dass sich Prozentangaben auf eine Grundmenge beziehen können.
Das Thema Direkte Proportionalität solltest du verstanden haben.
Du solltest gut mit Bruchzahlen umgehen und mit ihnen rechnen können.
Kursdauer
3 Stunden (wenn du alle Aufgaben selbstständig lösen möchtest)
2 Prozentrechnung im Alltag
Im Alltag ist es oft sinnvoll, die Prozentdarstellung zu verwenden, um Angaben mit anderen Werten vergleichen zu können.
Ein Beispiel ist die folgende Umfrage:
In Berlin und München wurden Leute befragt, ob sie eine Katze besitzen. Das Ergebnis ist in dieser Tabelle dargestellt:
Katzenbesitzer | Anzahl d. Befragten | |
|---|---|---|
Berlin | 17908 | 51224 |
München | 479 | 1276 |
Ist der Anteil der Katzenbesitzer in Berlin größer als in München?
Für eine anschauliche Antwort auf diese Frage ist die Berechnung des Anteils in Prozent sinnvoll.

Manchmal ist die Prozentangabe bereits bekannt, du möchtest aber die absoluten Werte wissen.
Hier entsprechen die g enthaltener Zucker der empfohlenen Tageszufuhr. Interessant wäre es, zu wissen, wie viel Zucker du pro Tag essen solltest. Dies ist der Grundwert, auf den sich die beziehen.
Wie du unter anderem diesen Grundwert berechnen kannst, lernst du im Folgenden.

3 Grundwert, Prozentwert und Prozentsatz
Du weißt bereits, dass sich Prozentzahlen im Alltag meistens auf einen Grundwert beziehen. Solche Begriffe sind wichtig, um über Prozentrechnung reden zu können. Deshalb werden nun die wichtigsten Begriffe mit einem Beispiel eingeführt:
Ein Eichhörnchen vergräbt 500 Nüsse,
→ 500 Nüsse sind hier der Grundwert G.
von denen es im Winter 400 Nüsse wiederfindet.
→ 400 Nüsse sind hier der Prozentwert W.
Das sind der vergrabenen Nüsse.
→ 80 % sind hier der Prozentsatz p.

Der Grundwert G ist die Bezugsgröße (hier 500 Nüsse) für Prozentwert und Prozentsatz. Er entspricht .
Der Prozentwert W hat die gleiche Einheit wie der Grundwert (hier also Nüsse). Der Prozentwert kann kleiner oder auch größer als der Grundwert sein.
Der Prozentsatz p ist das Verhältnis zwischen Prozentwert und Grundwert. Er wird in Prozent angegeben.
Laden
4 Zusammenhang zwischen Prozentwert und Prozentsatz
Wie Prozentwert und Prozentsatz zusammenhängen, kannst du an folgendem Beispiel nachvollziehen:
Die Anzahl der Blätter an der alten Eiche am Stadtrand ändert sich über die Jahreszeiten. Im Frühjahr trägt sie 40 000 Blätter.
Um die Blätterzahlen über die Jahreszeiten hinweg vergleichen zu können, kannst du die Anzahl im Frühjahr als Grundwert G festlegen, der dann den Vergleichswert bildet.

Nun besitzt der Baum zu Beginn des Sommers zunächst 48 000 Blätter (das entspricht , also 120 %, der 40000 Blätter) und erreicht später mit 60 000 (, also 150 %) Blättern seine volle Krone. Im Herbst schrumpft diese Zahl auf 24 000 (, also 60 %) und später noch weiter auf
4000 (, also 10 %).
Diese Zahlen können dann als Prozentwerte W (bzw. Prozentsätze p) festgelegt werden.
In der folgenden Tabelle hast du eine Übersicht über die Werte und kannst den besonderen Zusammenhang zwischen W und p erkennen:
Prozentwert | Prozentsatz | Quotient |
|---|---|---|
4 000 | 10 % | 40 000 |
24 000 | 60 % | 40 000 |
48 000 | 120 % | 40 000 |
60 000 | 150 % | 40 000 |
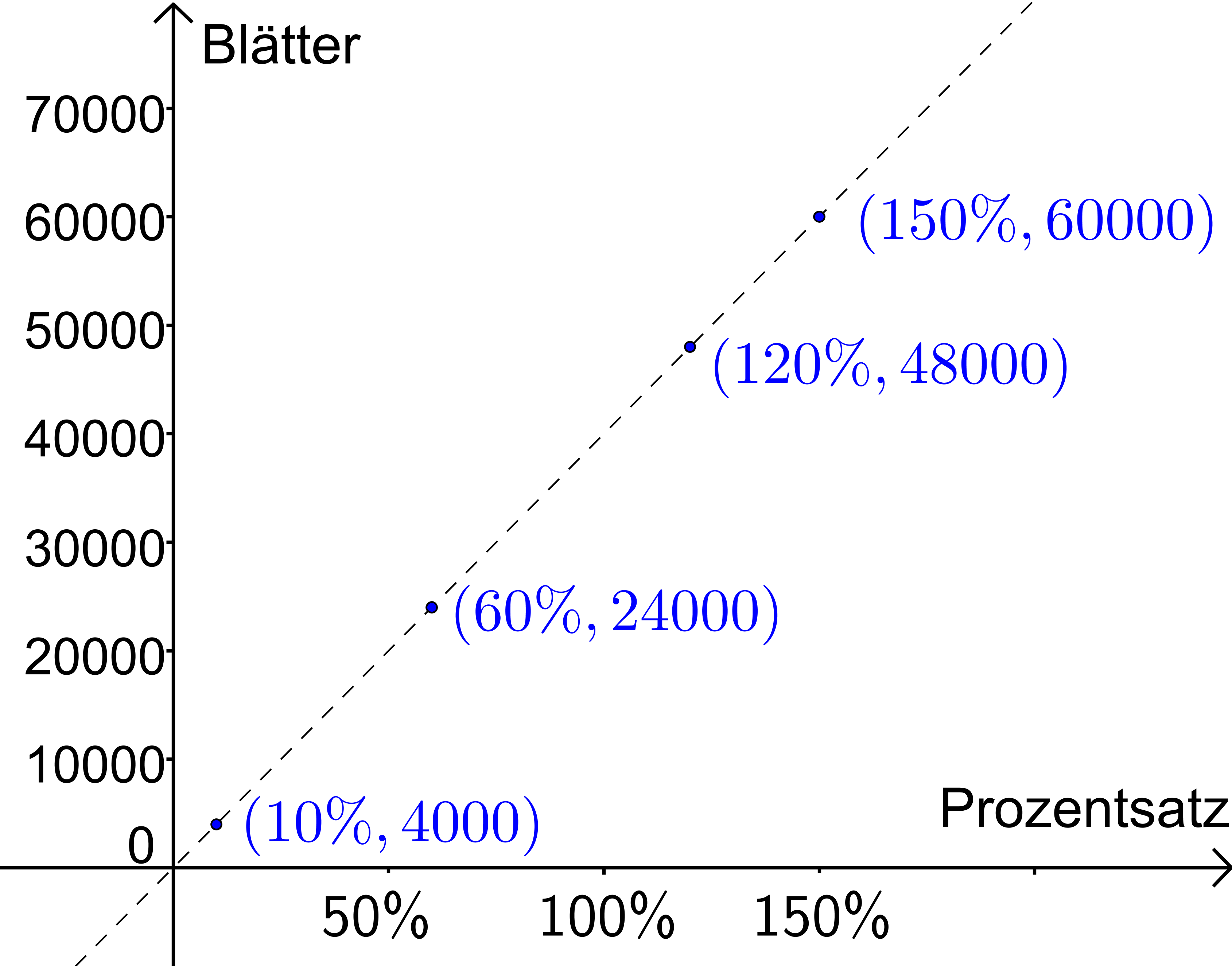
Wenn du W durch p oder umgekehrt teilst, erhältst du immer denselben Wert, nämlich den Grundwert oder dessen Kehrwert. In einem Koordinatensystem erkennst du dann eine Ursprungsgerade. Wie du schon weißt, bedeutet das, dass ein Vielfaches von W demselben Vielfachen von p entspricht. Mathematisch wird das wie folgt ausgedrückt:
5 Erinnerung Dreisatz
Hier findest du eine kurze Erklärung, wie der Dreisatz funktioniert. Falls du mit dem Dreisatz umgehen kannst, kannst du diese Seite auslassen.
Beim Dreisatz begegnest du einem Ausgangswert, der sich direkt proportional zu einem Vergleichswert verhält.
Beispiel: entsprechen .
In diesem Fall sind der Ausgangswert, sind der Vergleichswert.
Wird nun der Ausgangswert verändert, stellt sich die Frage, wie sich der Vergleichswert ändert. Beispiel: Jetzt hast du . Wie viele sind das? Dazu geht man einen kleinen Umweg und schaut, wie viel entsprechen.
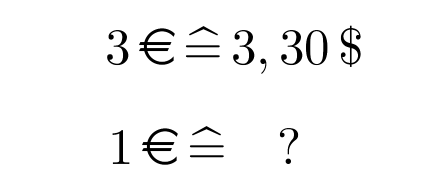
Du schreibst dazu die dir bekannte Entsprechung auf. Anschließend teilst du beide Werte durch den Ausgangswert, von dem dir die Änderung bekannt ist. Im Beispiel: Du weißt, dass du durch 3 teilen musst, um von auf zu kommen, also teilst du beide Seiten durch 3. Dadurch erhältst du auf der linken Seite genau eine Einheit, mit der du später weiterrechnen kannst. Also: entspricht .
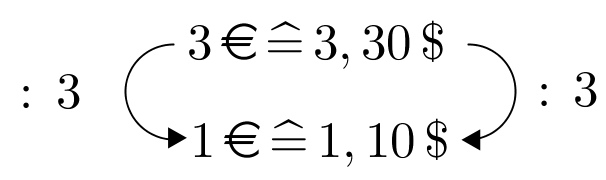
Zum Schluss multiplizierst du beide Zahlen mit dem gesuchten Wert. Im Beispiel: Multipliziere mit 7. Also: entsprechen .
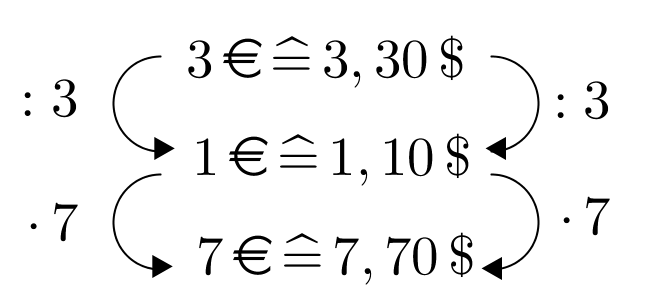
6 Prozentsatz berechnen (1/2)
Du hast nun den Prozentsatz und seinen Zusammenhang zum Prozentwert kennengelernt. Da der Prozentwert direkt proportional zum Prozentsatz ist, verhält sich der Prozentwert zum Prozentsatz genauso wie der Grundwert zu . Über einen Dreisatz kannst du den Prozentsatz somit berechnen.
Beispiel 1
Bei der Klassensprecherwahl bekommt Elisabeth 10 Stimmen. Insgesamt wurden 25 Stimmen abgegeben. Wie viel Prozent der Stimmen erhält Elisabeth?
25 Stimmen sind der Grundwert.
Zurückrechnen auf eine Stimme.
Hochrechnen auf 10 Stimmen.
Nun kann man den Prozentsatz ablesen.
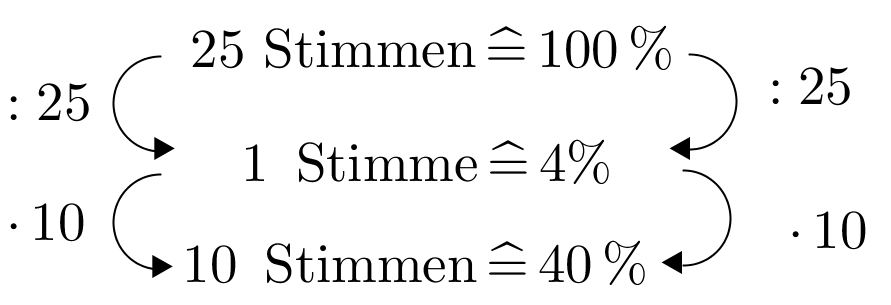
Beispielaufgaben
Berechne den Prozentsatz mittels Dreisatz!
Laden
Laden
Laden
7 Prozentsatz berechnen (2/2)
Berechnung über Formeln
Du kannst den Prozentsatz statt wie zuvor mit dem Dreisatz auch mit einer Formel berechnen.
Der Prozentsatz gibt das Verhältnis von Prozentwert zum Grundwert an. Dieses berechnest du wie in der Bruchrechnung, indem du den Prozentwert durch den Grundwert dividierst.
Beispiel 1
Gegeben | Würfe Würfe | Die Trefferquote ist der Anteil der Treffer an den Wurfversuchen. Als Grundwert musst du also die Wurfversuche wählen. Die Treffer sind dann der Prozentwert. |
|---|---|---|
Gesucht | Gesucht ist die Trefferquote. Also die Quote der Treffer pro Versuche. Das ist genau der Prozentsatz. | |
Lösung | Mit den Werten berechnest du die Trefferquote/den Prozentsatz und gibst diesen in Prozent an. | |
Antwort | Bettina hat eine Trefferquote von . |
Beispiel 2
Lukas bekommt von seiner Mutter 10 Euro zum Mittagessen. Eine Pizza mit Getränk kosten in der Pizzeria neben der Schule 9 Euro. Weil die Bedienung sehr nett war, bezahlt er trotzdem 10 Euro. Wie viel Prozent des eigentlichen Preises hat er gezahlt?

Gegeben | Die gesuchte Prozentangabe bezieht sich auf den eigentlichen Preis. Also ist der eigentliche Preis der Grundwert, von dem du ausgehst. Du vergleichst das tatsächlich Gezahlte mit dem eigentlichen Preis, also deinem Grundwert. Damit ist das tatsächlich Gezahlte der Prozentwert. | |
|---|---|---|
Gesucht | Gesucht ist der Prozentsatz. | |
Lösung | Mit den Werten berechnest du den Prozentsatz. | |
Antwort | Lukas hat ca. des eigentlichen Preises gezahlt. |
Übungsaufgaben
Berechne den Prozentsatz mittels Formel:
Laden
Laden
Laden
8 Übungsaufgaben zum Prozentsatz
Laden
Laden
9 Prozentwert berechnen (1/2)
Genauso wie den Prozentsatz kannst du den Prozentwert über den Dreisatz berechnen.
Berechnung über Dreisatz
Im Supermarkt gibt es 1,5 Liter Packungen Apfelnektar mit einem Fruchtgehalt von . Wie viel Liter Frucht sind dies?
1,5 Liter sind der Grundwert.
Zurückrechnen auf
Hochrechnen auf
Nun kann man den Prozentwert ablesen.
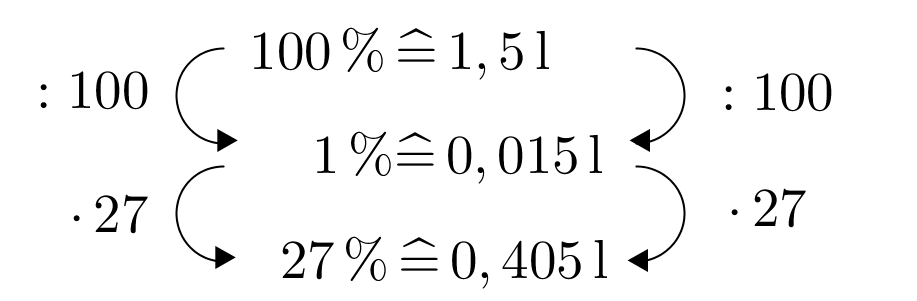
Zur Übung:
Berechne den Prozentwert. Wie viel sind …
Laden
10 Prozentwert berechnen (2/2)
Berechnung über Formel
Der Prozentwert kann auch wieder über eine Formel berechnet werden.
Aus der Bruchrechnung weißt du, wie man mit Verhältnissen rechnet. Zum Beispiel bedeutet , dass man
rechnen muss.
Statt eines Bruches gibt nun der Prozentsatz an, in welchem Verhältnis der Prozentwert zum Grundwert steht.
Beispiel: Wie viel sind von 200 Äpfeln?
Also:

Genau so kannst du immer den Prozentwert ausrechnen. Als Formel schreibt man das wie folgt:
Zwei Formeln für die Prozentrechnung? Nein!
Die Formel zur Berechnung des Prozentwertes und die zur Berechnung des Prozentsatzes ist die gleiche! Sie wurde nur mit einer Umkehrrechnung umgestellt.
Beispiel: Wie viel sind von 200 Äpfeln?
Mit der Formel vom Prozentsatz würdest du schreiben:
bzw.
Die Umkehrrechnung ergibt:
Wie du siehst, erhält man auch mit der Formel vom Prozentsatz die gleiche Rechnung wie vorhin.
Beispielaufgabe
Jeder Mensch besteht zu etwa aus Wasser. Thomas wiegt . Wie viel wiegt das Wasser in seinem Körper?
Gegeben | |
|---|---|
Gesucht | |
Lösung | |
Antwort | Das Wasser in Thomas' Körper wiegt . |
Zur Übung:
Berechne den Prozentwert. Wie viel sind …
Laden
Laden
Laden
11 Übungsaufgaben zum Prozentwert
Laden
Laden
12 Grundwert berechnen (1/2)
Den Grundwert kannst du mit denselben Mitteln berechnen wie den Prozentsatz und den Prozentwert.
Berechnung über Dreisatz
Die Polizei kontrolliert Fahrräder. 128 Fahrräder haben kein Licht, das sind . Wie viele Fahrräder wurden kontrolliert?
Gegeben sind die Anzahl der beanstandeten Fahrräder, also der Prozentwert, und der Prozentsatz.
Zurückrechnen auf
Hochrechnen auf
Nun kann man den Grundwert unten rechts ablesen.
Antwort: Es wurden 800 Fahrräder kontrolliert.

Zur Übung:
Laden
Laden
13 Grundwert berechnen (2/2)
Berechnung über Formel
Herleitung
Die Formel für die Berechnung des Grundwertes lässt sich aus den Formeln für die Berechnung von Prozentwert oder Prozentsatz herleiten. Die Formel
bzw.
kann man wie im vorherigen Teil umformen zu:
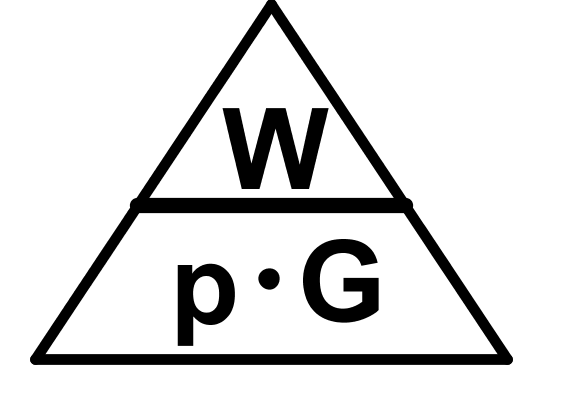
Formeldreieck
Das Formeldreieck ist eine nützliche Merkhilfe, aus der man sich die Formeln für Prozentwert, Prozentsatz und Grundwert schnell herleiten kann. Man deckt einfach die Größe, deren Formel man sich herleiten will, ab. Nun betrachtet man den Rest des Dreiecks und liest die Formel ab (Der Strich wird ggf. zu einem Bruchstrich).
Beispiel
Ein Fahrkartenkontrolleur kontrolliert in der U-Bahn.
64 Fahrgäste haben kein Ticket, das sind . Wie viele Passagiere wurden kontrolliert?
Gegeben | Fahrgäste und |
|---|---|
Gesucht | : Anzahl der Fahrgäste insgesamt |
Lösung | Fahrgäste |
Zur Übung:
Laden
Laden
14 Übungsaufgaben zum Grundwert berechnen
Laden
Laden
Laden
15 Zusammenfassung
Was sind Grundwert, Prozentwert und Prozentsatz?
Der Grundwert G ist die Bezugsgröße für Prozentwert und Prozentsatz. Er entspricht .
Der Prozentwert W ist eine Menge von der Art des Grundwertes. Diese kann kleiner oder auch größer sein.
Der Prozentsatz p ist das Verhältnis zwischen Prozentwert und Grundwert. Er wird in Prozent angegeben.
Wie hängen Grundwert, Prozentwert und Prozentsatz zusammen?
Der Prozentwert und Prozentsatz sind direkt proportional.
Der Quotient von Prozentwert und dem zugehörigen Prozentsatz ergibt immer den Grundwert.
Wie berechnet man Grundwert, Prozentwert und Prozentsatz?
Mit einer Formel
Aus dem Formeldreieck kannst du die drei Umstellungen der Formel ablesen:

Mit dem Dreisatz
Mit dem Dreisatz kann man aus einem gegebenen Verhältnis auf ein unbekanntes schließen.
Sobald man zwei der drei Größen Grundwert, Prozentwert und Prozentsatz gegeben hat, kann man ihn anwenden.
Mit zwei meist einfachen Rechenschritten erhält man die gesuchte Größe.
16 Zeig, was du kannst!
Laden
Laden
Laden
Laden
Laden
Hier findest du weitere Aufgaben zu Grundwert, Prozentwert und Prozentsatz.

