1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, was Vektoren sind und wie man mit ihnen rechnen kann.
Vorkenntnisse
Du solltest die Grundrechenarten beherrschen und dich mit den Grundbegriffen der Geometrie auskennen.
Kursdauer
Der Kurs dauert ungefähr 2 Stunden, wo du verschiedene Vektoren kennenlernst und Aufgaben bearbeiten kannst.
2 Was ist ein Vektor? (1/4)
Wir haben gestern gemeinsam einen Schatz vergraben und auf einer Karte die richtige Stelle mit einem Kreuz markiert.
Nun wollen wir eine Schatzkarte erstellen, damit unsere Freunde den Schatz suchen können.
Wir sollten uns also einen Weg überlegen, der an gut erkennbaren Punkten vorbeiführt, und diesen mit Pfeilen auf der Karte einzeichnen.

Nehmen wir doch die Felsen am Fuß der Berge als Startpunkt. Danach führen wir unsere Freunde am Wegweiser und dem großen Baum vorbei zum Schatz.
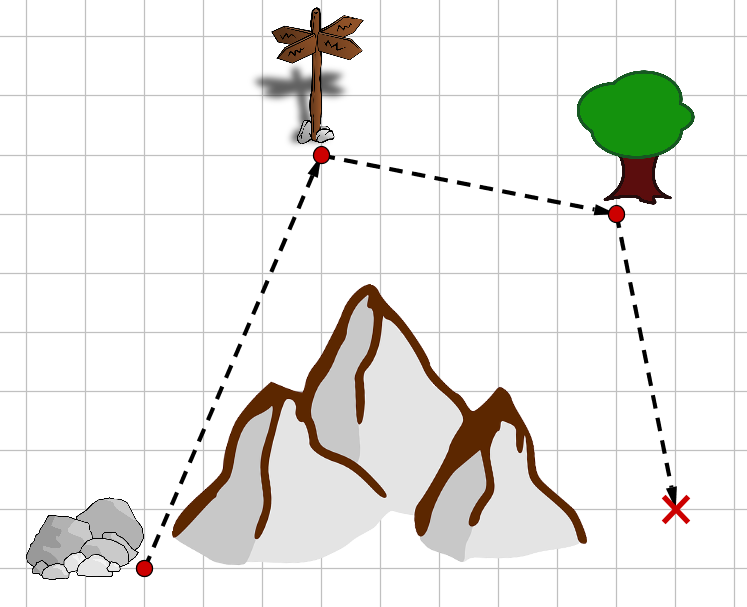
3 Was ist ein Vektor? (2/4)
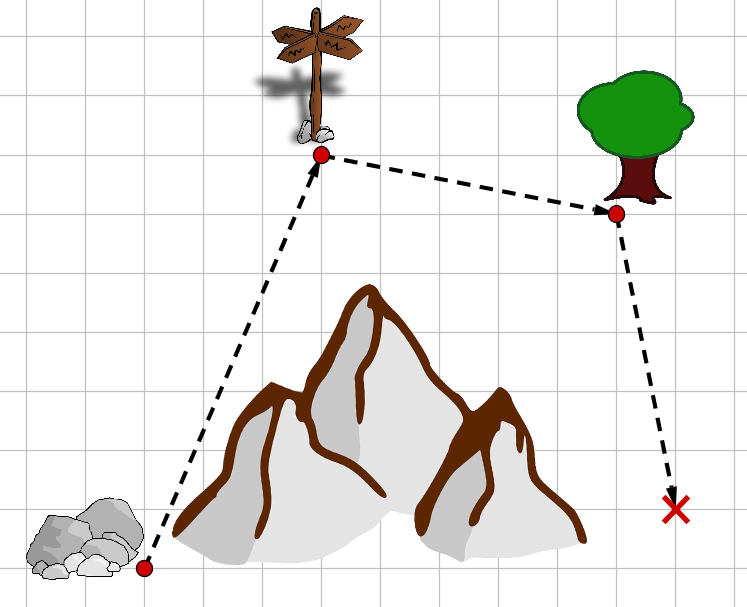
Nun wollen wir uns überlegen, welche Eigenschaften die Pfeile haben, die wir auf unserer Karte eingezeichnet haben. Die ersten beiden Pfeile (also der Pfeil von den Felsen zum Wegweiser und vom Wegweiser zum Baum) haben wir durch ihren Anfang und ihr Ende festgelegt.
Das heißt, unsere Freunde werden wissen, was sie zu tun haben, wenn wir ihnen auftragen, von den Felsen zum Wegweiser und von dort aus weiter zum Baum zu laufen.
Der dritte Teil des Weges ist allerdings nicht so leicht zu erklären. Auf der Karte gibt es zwar ein Kreuz, aber eben auch nur auf der Karte. Wir können also nicht sagen: „Geht vom Baum weiter zum Kreuz.“ Das heißt, wir müssen eine andere Möglichkeit finden.
4 Was ist ein Vektor? (3/4)
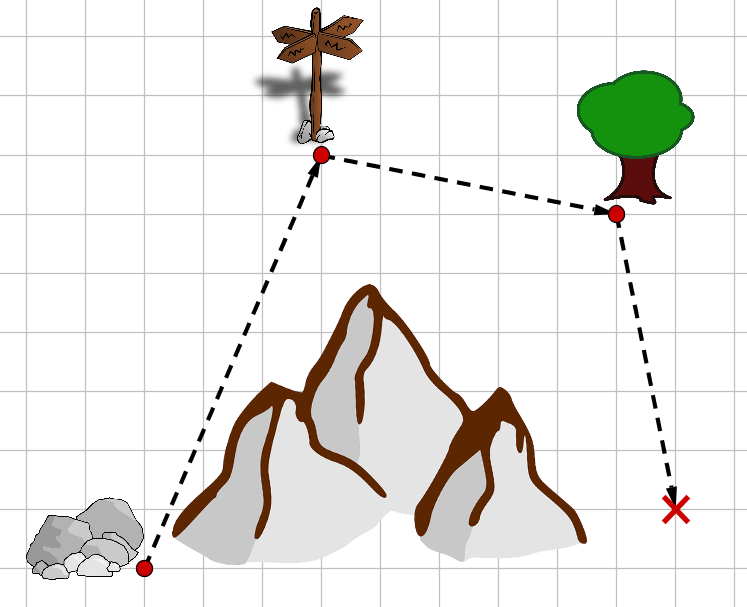
Wie du siehst, ist auf der Karte ein Gitternetz eingezeichnet. Das gibt es zwar nicht in Wirklichkeit, aber es lässt sich gut in Entfernungen umrechnen. Die Länge eines Kästchens auf unserer Karte soll Schritten in Wirklichkeit entsprechen (Maßstab). Das heißt, wenn du wissen willst, wo der Punkt Kästchen oberhalb vom Wegweiser wirklich ist, musst du vom Wegweiser Schritte nach Norden laufen.
Damit wollen wir jetzt erklären, wo unser Schatz vergraben ist. Auf der Karte ist er Kästchen unterhalb und Kästchen rechts des Baumes vergraben. Wir tragen unseren Freunden also auf, vom Baum aus Schritte nach Süden und Schritte nach Osten zu laufen.
Um also den Pfeil festzulegen, ohne den Endpunkt zu kennen, gehen wir davon aus, dass wir uns am Startpunkt des Pfeils befinden. Dann beschreiben wir, wo von dort aus gesehen der Endpunkt des Pfeils liegt.
5 Was ist ein Vektor? (4/4)
Um den letzten Teil unseres Weges zu beschreiben, haben wir also gewissermaßen seine Koordinaten angegeben, denn wir haben uns überlegt, welche Länge der Pfeil in Nord-Süd- bzw. West-Ost-Richtung hat. Unsere Pfeile können wir auch als Vektoren bezeichnen.
Vektoren zeichnen sich nämlich ebenfalls durch ihre beiden Koordinaten aus. Üblicherweise sind es bei Vektoren die - und -Koordinate. Man spricht auch manchmal von der - und -Komponente.
Möchte man die Koordinaten des folgenden Vektors angeben, geht man wie folgt vor:
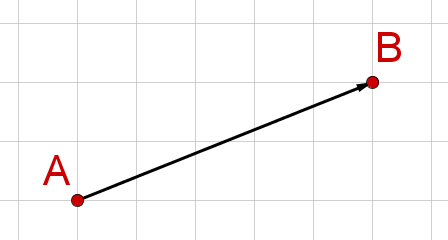
liegt Kästchen rechts und Kästchen oberhalb von . Dadurch ist der Vektor bestimmt und wir schreiben ihn als , denn wie im Koordinatensystem werden Werte nach rechts bzw. oben als positive und Werte nach links bzw. unten als negative Koordinaten betrachtet.
Außerdem wollen wir dem Vektor noch einen Namen geben, wie z. B. "" und "" für die beiden Punkte. Für Vektoren verwendet man gerne Kleinbuchstaben mit einem kleinen Pfeil darüber. Damit gilt also:
6 Video zur Einführung des Vektorbegriffs
In diesem Video wird der Vektorbegriff noch einmal erklärt. Wenn du dich schon sicher fühlst, kannst du das Video auch überspringen und gleich die Aufgaben auf der nächsten Seite versuchen.
Laden
7 Aufgaben
Laden
8 Repräsentant
Vektoren sind nur dadurch bestimmt, wie lang sie sind und in welche Richtung sie zeigen.
Man sieht die Pfeile im Bild rechts wieder als Vektoren an und betrachtet den mit gekennzeichneten genauer. Er führt um Kästchen nach rechts und Kästchen nach unten.
Vergleicht man ihn mit den anderen Pfeilen, die in dem Koordinatensystem eingezeichnet sind, so sieht man, dass alle dieselben Koordinaten haben, denn alle zeigen Kästchen nach rechts und Kästchen nach unten.
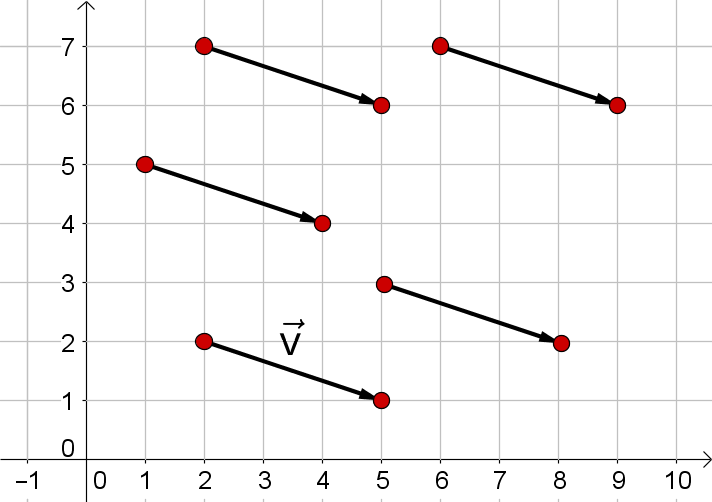
Ein Vektor wird durch seine Koordinaten festgelegt, somit ist im obigen Bild fünfmal derselbe Vektor abgebildet. Jeder einzelne der Pfeile wird als Repräsentant von bezeichnet.
Jeder Vektor hat beliebig viele verschiedene Repräsentanten.
9 Aufgaben zu Repräsentant
Laden
10 Aufstellen des Vektors zwischen zwei Punkten
Die Koordinaten eines Vektors, dessen Repräsentant in einem Gitternetz eingezeichnet ist, können einfach anhand der Kästchen abgezählt werden.
Dies funktioniert auch in einem Koordinatensystem. Allerdings sind Vektoren oft nur dadurch gegeben, dass die Koordinaten zweier Punkte (z.B. und genannt) angegeben werden, zwischen denen ein Repräsentant des Vektors verläuft.
In diesem Fall bezeichnet man den Vektor auch mit . Zeigt von nach , so heißt Fuß oder Fußpunkt und Spitze von .
Möchte man nun die Koordinaten des Vektors berechnen, der von nach zeigt, geht man wie folgt vor:
Allgemein ausgedrückt hält man sich an den Merksatz
Man rechnet "Spitze minus Fuß".
Das heißt man erhält die -Koordinate von , indem man von abzieht. Entsprechend erhält man die -Koordinate, indem man von abzieht. Man erhält also:

11 Beispiel: Aufstellen des Vektors zwischen zwei Punkten
Beispiel
Bestimme die Koordinaten des Vektors, dessen Repräsentant von Punkt nach Punkt verläuft.
Lösung: Nach der Formel werden jeweils die Werte des Fußpunktes () von den Werten der Spitze () abgezogen.
Anschauliche Darstellung
Im folgenden Applet kannst du den abgebildeten Vektor (bzw. eigentlich einen von dessen Repräsentanten) und auch dessen Fuß und Spitze einzeln in einem Koordinatensystem umherschieben. Im rechten Kasten kannst du dann beobachten, wie sich der eigentliche Vektor und dessen Koordinaten verändern.
Hier kannst du nochmals sehr gut den Unterschied zwischen Vektor und Repräsentant sehen. Verschiebst du den Repräsentanten als ganzes, so ändern sich die Koordinaten des Vektors nicht und somit auch der Vektor selbst nicht. Erst wenn du entweder den Fuß oder die Spitze einzeln verschiebst und somit die Länge und Ausrichtung des "Pfeils" veränderst, ändert sich auch der Vektor.
12 Aufgaben: Aufstellen des Vektors zwischen zwei Punkten
Laden
Laden
13 Nullvektor
Ein besonderer Fall eines Vektors ist der Nullvektor: . Einen Pfeil zu zeichnen, der diesen Vektor repräsentiert, ist natürlich nicht möglich, denn der Nullvektor zeigt in keine Richtung und hat die Länge Null.
Anschaulich
Man kann sich unter dem Nullvektor die Bewegung von einem Punkt zu sich selbst vorstellen.
Versuche einmal, im Applet, das du unten ausklappen kannst und das du schon von der Kursseite Beispiel:Aufstellen des Vektors zwischen zwei Punkten kennst, einen Nullvektor zu erstellen, indem du beide Punkte und auf dieselbe Stelle ziehst (Das muss nicht der Ursprung sein!). Das bedeutet, dass Fußpunkt und Spitze des Repräsentanten zusammenfallen. Du wirst sehen, dass der eingezeichnete Pfeil verschwindet.
14 Gegenvektor
Wenn ein Vektor gegeben ist, so bezeichnet man den entgegengesetzten Vektor als Gegenvektor . Anschaulich: Dreht man den Vektor um erhält man den Gegenvektor .
Der Gegenvektor hat also dieselbe Länge wie der gegebene Vektor.
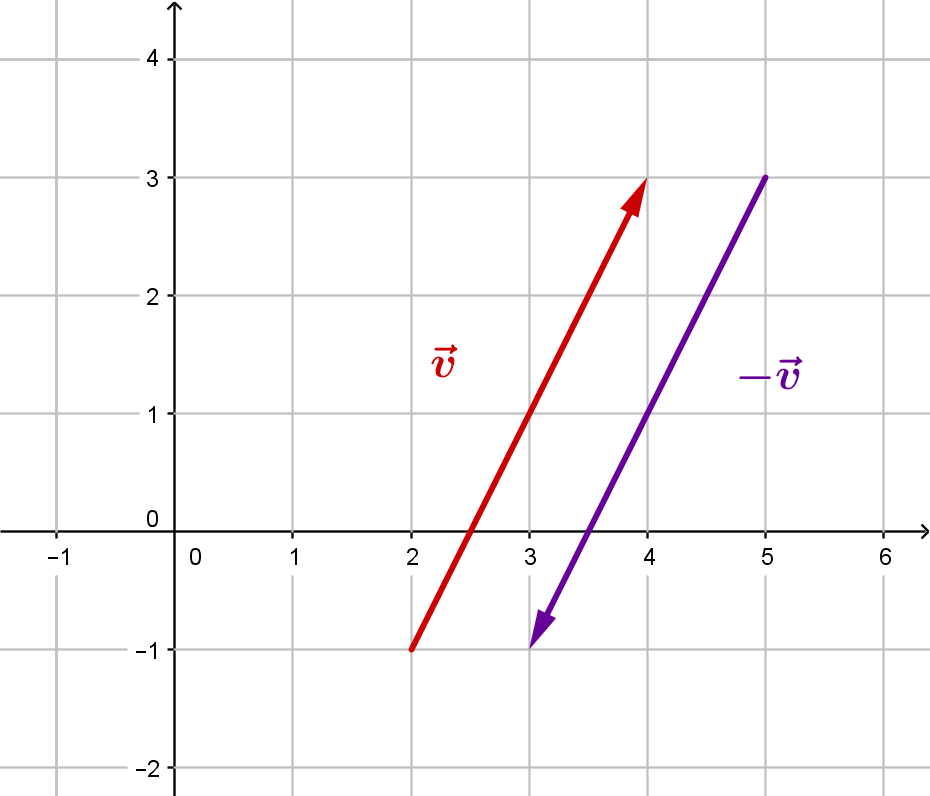
Beispiel
Hat man den Vektor gegeben, so ist der Gegenvektor einfach derselbe Vektor mit den umgekehrten Vorzeichen, also .
15 Aufgabe: Gegenvektor
16 Ortsvektor
Wie in diesem Kurs bereits erwähnt wurde, kann man einen Vektor , dessen Repräsentant zwischen zwei Punkten und verläuft, auch als bezeichnen.
Handelt es sich beim "Startpunkt" um den Koordinatenursprung , bezeichnet man als den Ortsvektor des Punkts .
Die Koordinaten des Vektors sind dieselben Koordinaten, die auch der Punkt hat.
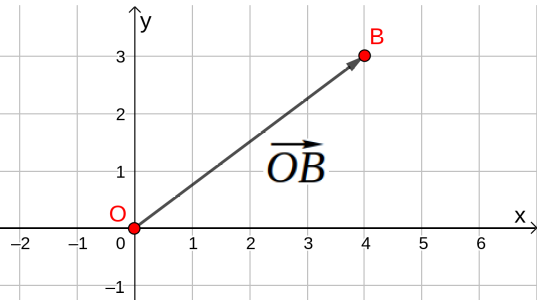
Da man die Repräsentanten von Vektoren an jeden beliebigen Ort im Koordinatensystem verschieben kann, gibt es zu jedem Vektor auch immer einen Repräsentanten, der einen Ortsvektor darstellt. Es handelt sich dabei um den Repräsentanten, dessen Fußpunkt der Ursprung ist.
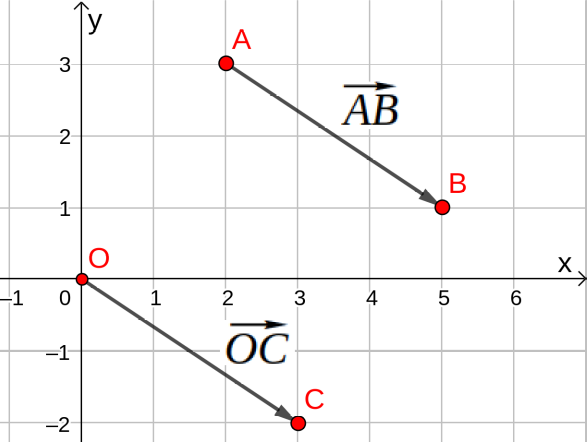
Beispiel: Der Vektor der von nach verläuft kann auch als Ortsvektor des Punktes angesehen werden.
17 Vergleich: Vektor - Punkt
Vergleicht man die Eigenschaften von Punkten und Vektoren, stellt man zusammenfassend Folgendes fest:
Sowohl Punkte als auch Vektoren in der Zeichenebene werden durch Koordinaten festgelegt. Allerdings werden diese unterschiedlich notiert. Die Koordinaten eines Punktes schreibt man als , die Koordinaten eines Vektors kann man sowohl in Zeilenform (wie Punkte) oder in Spaltenform angeben, als .
Punkte können ganz einfach in die Ebene eingezeichnet werden. Von Vektoren kann man lediglich einzelne Repräsentanten zeichnen.
Der Ort, an dem ein Punkt in der Ebene liegt, ist durch seine Koordinaten genau festgelegt. Repräsentanten eines Vektors dagegen können an jeder beliebigen Stelle des Koordinatensystems liegen.
Anschaulich: Mithilfe von Vektoren kann man Punkte verschieben.
Als "Schnittstelle" zwischen Vektoren und Punkten kann man die Ortsvektoren ansehen. Durch einen Ortsvektor ist der Punkt, der dieselben Koordinaten hat, eindeutig festgelegt.
18 Zusammenfassung
Ein Vektor gibt die Verschiebung oder Bewegung eines Objektes an. Befindet sich dieses Objekt in einem Gitternetz oder Koordinatensystem, so gibt man den Vektor mithilfe seiner Koordinaten an.
Zeichnet man den Vektor an einer beliebigen Stelle in ein Koordinatensystem ein, so handelt es sich dabei um einen Repräsentanten des Vektors.
Oft werden Vektoren mithilfe des Fußes und der Spitze eines Repräsentanten angegeben. Aus den Koordinaten der Punkte kann man mithilfe der Formel
die Koordinaten des gesuchten Vektors bestimmen.
Nullvektor
Der Vektor mit den Koordinaten wird als Nullvektor bezeichnet. Man spricht weiterhin von einer Verschiebung, auch wenn sich die Position des Objekts hier nicht verändert.
Gegenvektor
Bei dem Gegenvektor eines Vektors handelt es sich um denjenigen Vektor, der dieselbe Länge und Orientierung aufweist, allerdings in die entgegengesetzte Richtung zeigt. Er wird deshalb als aufgeschrieben.
Ortsvektor
Mithilfe des Ortsvektors kann die Position eines Punkts im Koordinatensystem ausgedrückt werden. Es handelt sich dabei um denjenigen Vektor, dessen Repräsentant den Ursprung mit dem Punkt verbindet. Zum Punkt erhält man den Ortsvektor .
19 Zeige, was du kannst!
Laden
