Bestimme den Flächeninhalt des Dreiecks mithilfe der Determinante
, und
FEFür diese Aufgabe benötigst Du folgendes Grundwissen: Determinante
Um den Flächeninhalt bestimmen zu können, brauchen wir erst die Vektoren und .
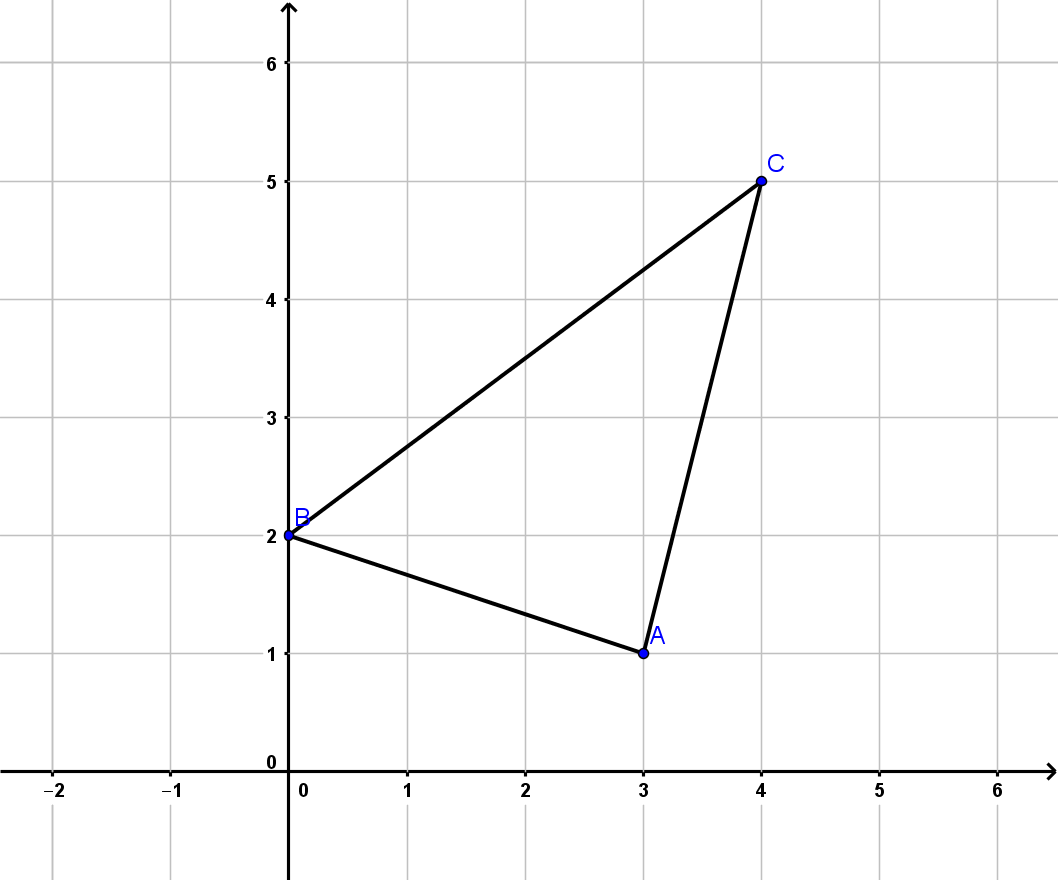
Nun setzt du die Vektoren in die Determinante ein, so dass für den Flächeninhalt gilt:
Beachte dabei, dass die Reihenfolge der Vektoren, die man in die Determinante einsetzt, gegen dem Uhrzeigersinn ist!
Für den Flächeninhalt des Dreiecks gilt also
Hast du eine Frage oder Feedback?
, und
FEFür diese Aufgabe benötigst Du folgendes Grundwissen: Determinante
Um den Flächeninhalt bestimmen zu können, brauchen wir erst die Vektoren und .
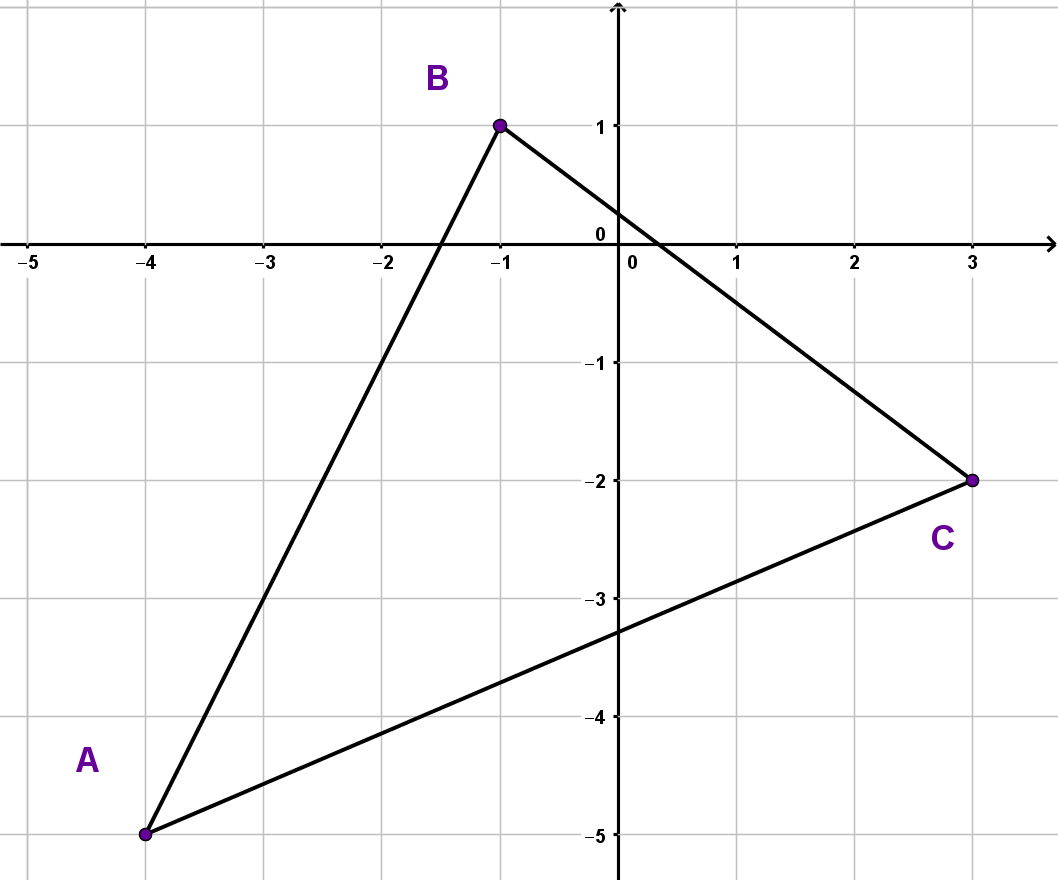
Nun setzt du die Vektoren in die Determinante ein, so dass für den Flächeninhalt gilt:
Beachte dabei, dass die Reihenfolge der Vektoren, die man in die Determinante einsetzt, gegen dem Uhrzeigersinn ist!
Für den Flächeninhalt des Dreiecks gilt also
Hast du eine Frage oder Feedback?
, und
FEFür diese Aufgabe benötigst Du folgendes Grundwissen: Determinante
Um den Flächeninhalt bestimmen zu können, brauchen wir erst die Vektoren und .
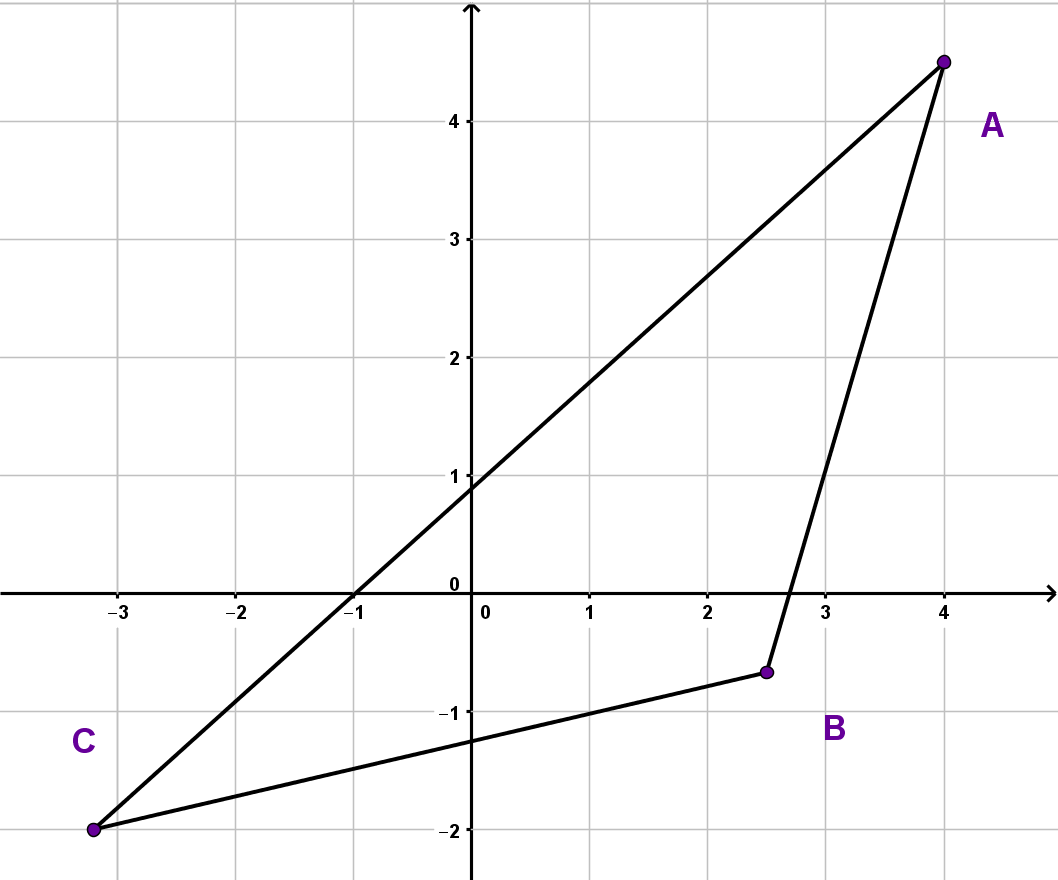
Nun setzt du die Vektoren in die Determinante ein, so dass für den Flächeninhalt gilt:
Beachte dabei, dass die Reihenfolge der Vektoren, die man in die Determinante einsetzt, gegen dem Uhrzeigersinn ist!
Für den Flächeninhalt des Dreiecks gilt also .
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
