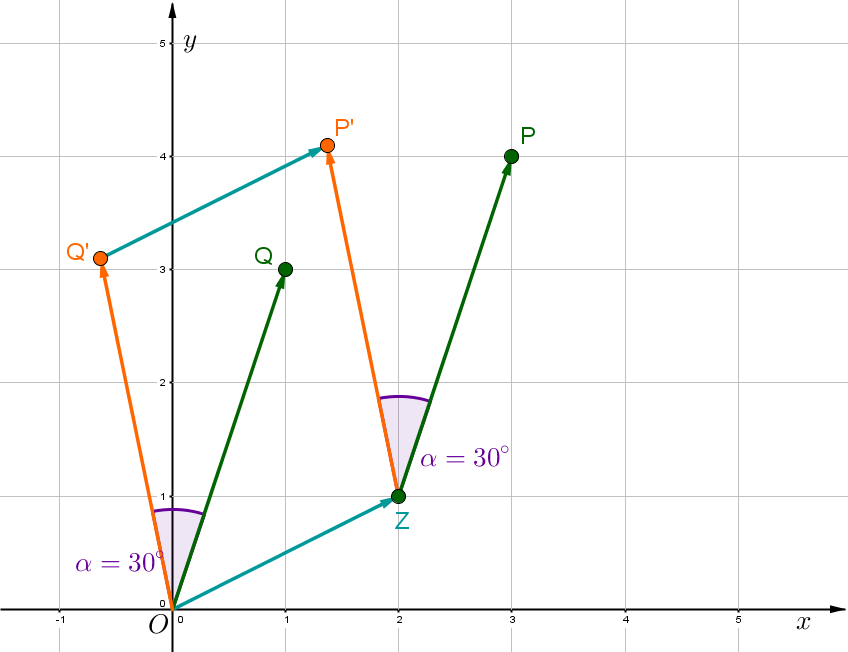
Bestimme den Punkt , den du durch eine Drehung des Punktes um das Zentrum mit dem Winkel erhältst.
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung eines Punktes um ein Zentrum
1. Schritt: Bestimme die Koordinaten des Hilfsvektors .
Setze die Koordinaten des Vektors ein.
2. Schritt: Drehe mit Winkel um den Ursprung.
Setze den Vektor und den Winkel ein.
Führe die Matrix-Vektor-Multiplikation durch.
3. Schritt: Verschiebe den Vektor um den Vektor .
Setze die Vektoren ein.
ist der gesuchte Punkt.
Hast du eine Frage oder Feedback?
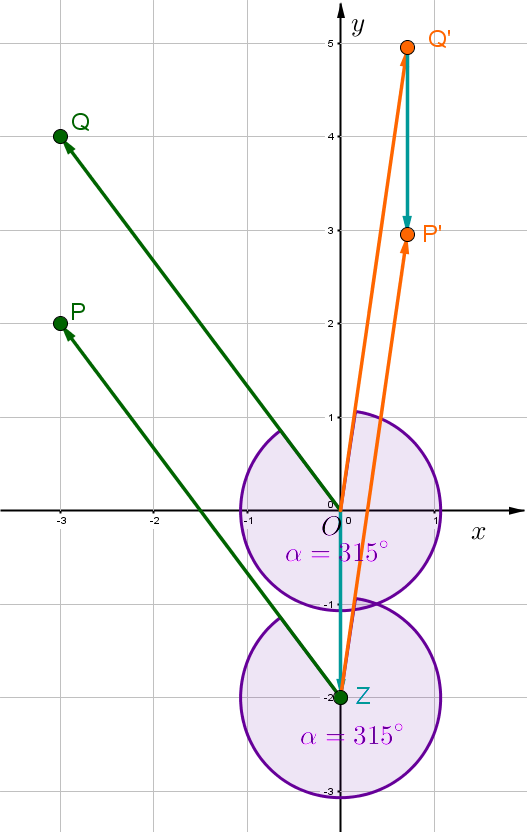
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung um einen Punkt
1. Schritt: Bestimme die Koordinaten des Hilfsvektors .
Setze die Koordinaten des Vektors ein.
2. Schritt: Drehe mit Winkel um den Ursprung.
Setze den Vektor und den Winkel ein.
Führe die Matrix-Vektor-Multiplikation durch.
3. Schritt: Verschiebe den Vektor um den Vektor .
Setze die Vektoren ein.
ist der gesuchte Punkt.
Hast du eine Frage oder Feedback?
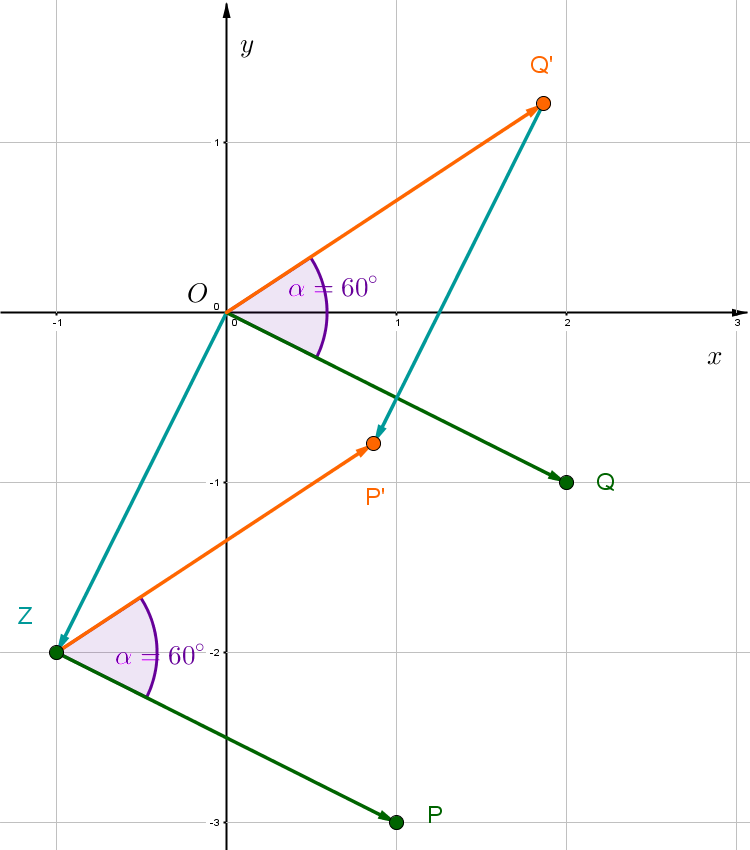
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung um einen Punkt
1. Schritt: Bestimme die Koordinaten des Hilfsvektors .
Setze die Koordinaten des Vektors ein.
2. Schritt: Drehe mit Winkel um den Ursprung.
Setze den Vektor und den Winkel ein.
Führe die Matrix-Vektor-Multiplikation durch.
3. Schritt: Verschiebe den Vektor um den Vektor .
Setze die Vektoren ein.
ist der gesuchte Punkt.
Hast du eine Frage oder Feedback?
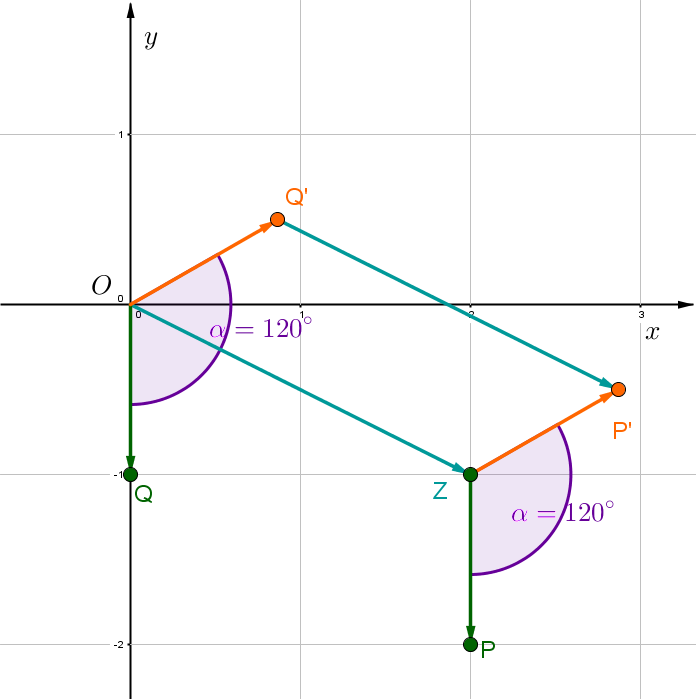
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung um einen Punkt
1. Schritt: Bestimme die Koordinaten des Hilfsvektors .
Setze die Koordinaten des Vektors ein.
2. Schritt: Drehe mit Winkel um den Ursprung.
Setze den Vektor und den Winkel ein.
Führe die Matrix-Vektor-Multiplikation durch.
3. Schritt: Verschiebe den Vektor um den Vektor .
Setze die Vektoren ein.
ist der gesuchte Punkt.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
