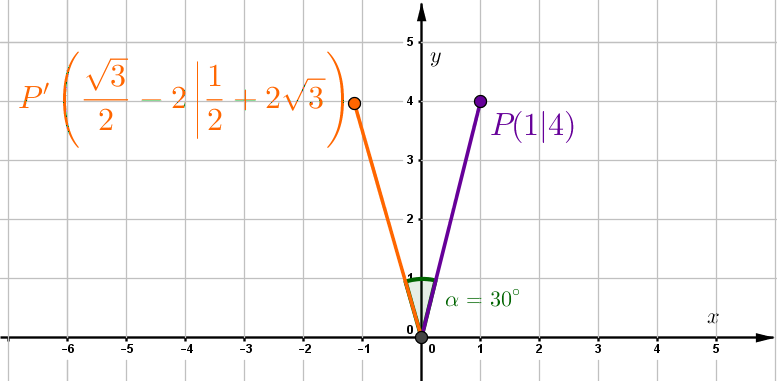Aufgaben zur Drehung mit Matrizen
Hier findest du Übungsaufgaben zur Drehung mithilfe von Matrizen. Wiederhole wichtige Grundlagen und vertiefe dein Wissen!
- 1
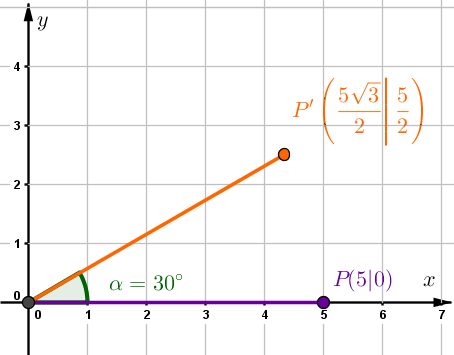
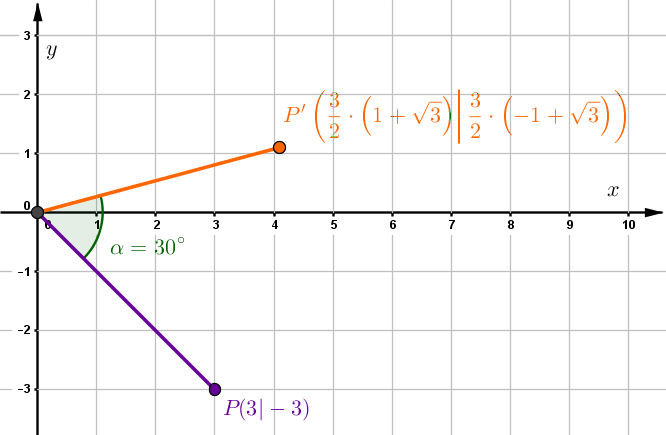
Bestimme die Abbildungsgleichung bei einer Drehung des Punktes um den Winkel um den Ursprung und die Koordinaten des dadurch abgebildeten Punktes .
- 2
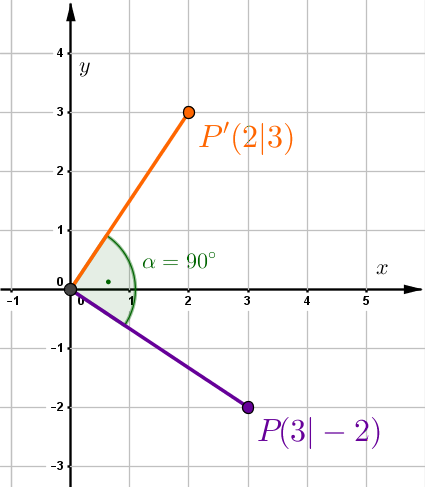
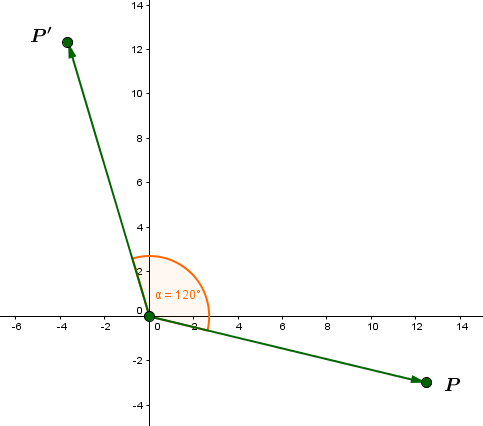
Berechne den Winkel , um welchen der Punkt zum Punkt gedreht wurde.
,
,
- 3
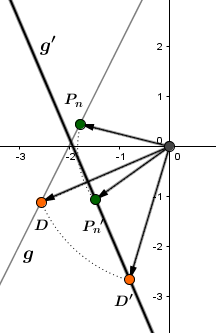
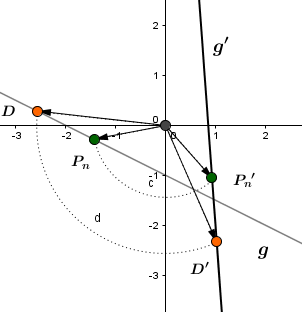
Die Gerade wird durch Drehung um den Ursprung mit dem Winkelmaß auf die Gerade abgebildet. Berechne die Geradengleichung von .
mit
mit
mit
- 4
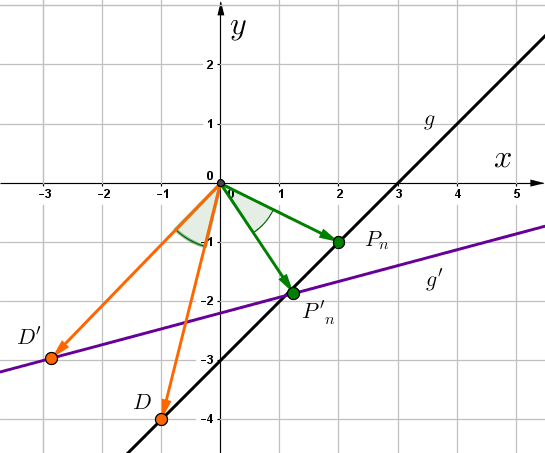
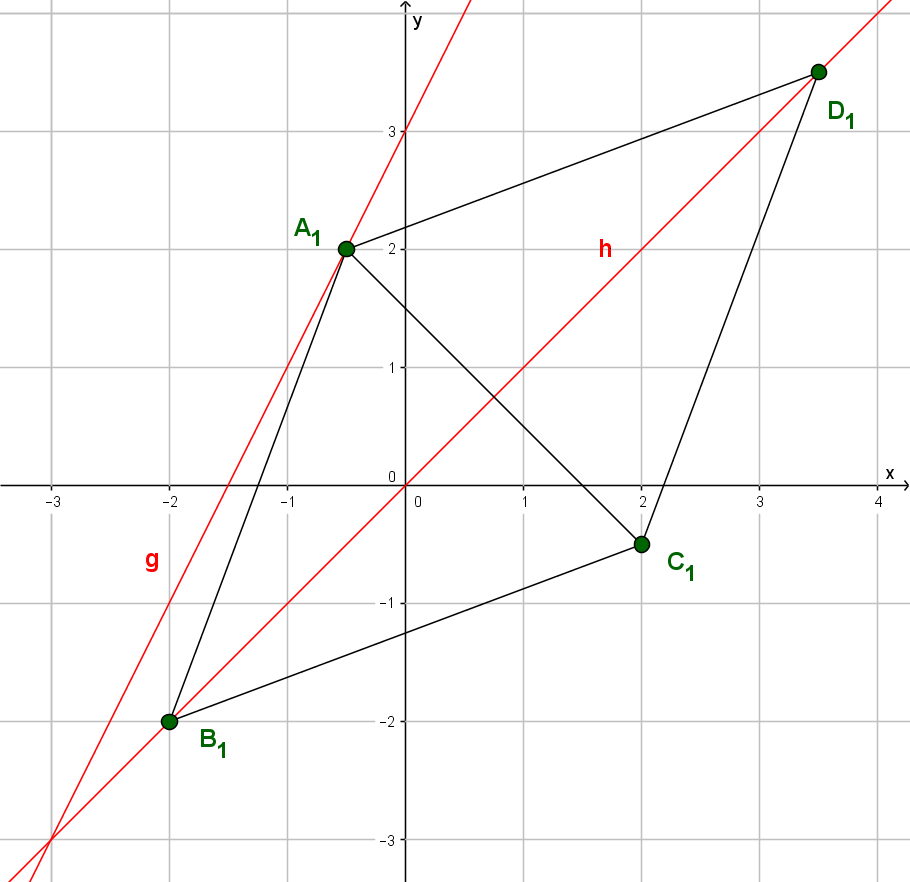
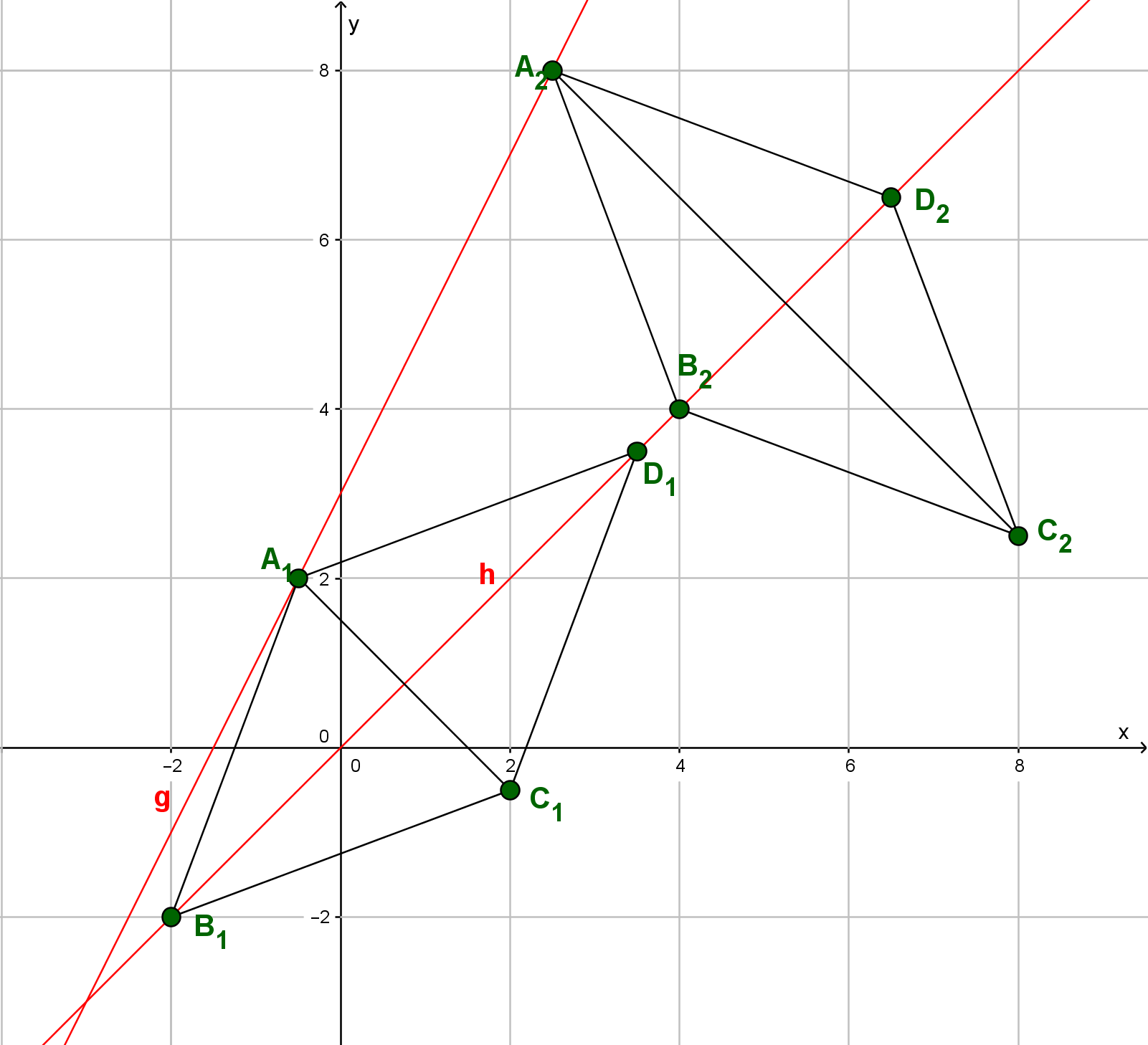
Der Graph zu mit definiert die Position der Punkte . Diese bilden zusammen mit und das Quadrat .
Links siehst du den Graphen mit den Quadraten für den Fall und für den Fall .
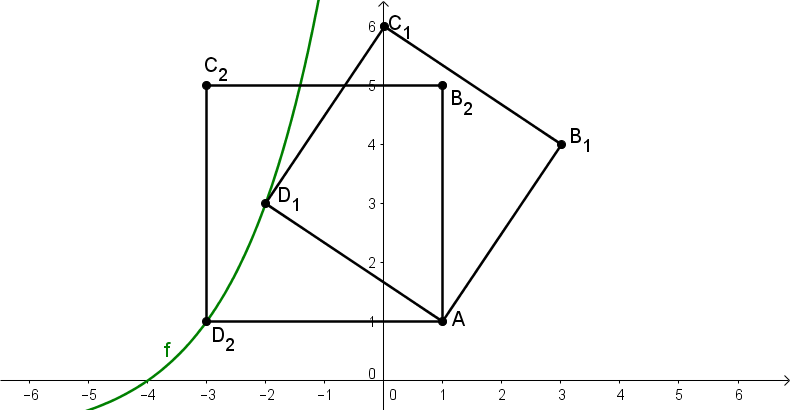
Zeige, dass für in Abhängigkeit von gilt: .
Überprüfe anschließend ob es für Punkte auf der x-Achse, bzw. y-Achse gibt.
- 5
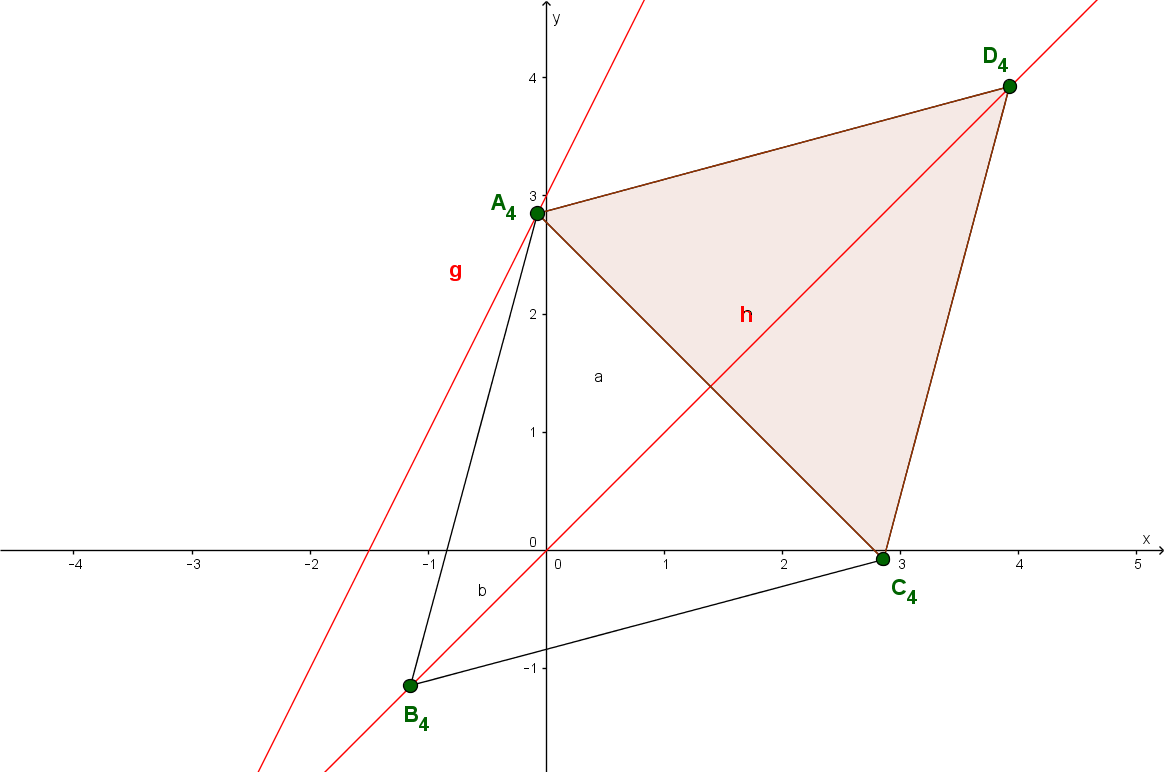
Die Gerade mit der Gleichung ist Symmetrieachse von Rauten . Die Diagonalen der Rauten liegen auf der Geraden . Die Punkte liegen auf der Geraden mit der Gleichung . Die Abszisse der Punkte ist stets um vier größer als die Abszisse der Punkte . Dabei gilt: -.
Runde im folgenden auf zwei Nachkommastellen!
Zeichne die Geraden und sowie die Raute für und die Raute für in ein Koordinatensystem! Für die Zeichnung: Längeneinheit ; .
Zeige, dass für die Punkte in Abhängigkeit von der Abszisse der Punkte gilt: ! Bestätige sodann durch Rechnung die untere Intervallgrenze der Rauten !
Begründe, warum sich für die obere Intervallgrenze ergibt und bestätige diese durch Rechnung!
Bestimme rechnerisch die Koordinaten der Punkte in Abhängigkeit von der Abszisse der Punkte !
Berechne den Flächeninhalt der Rauten in Abhängigkeit von der Abszisse der Punkte !
Die Seite der Raute verläuft senkrecht zur -Achse. Berechne die Koordinaten des Punktes !
In der Raute hat die Diagonale die gleiche Länge wie die Seite . Begründe, dass für die Diagonale gilt: !
- 6
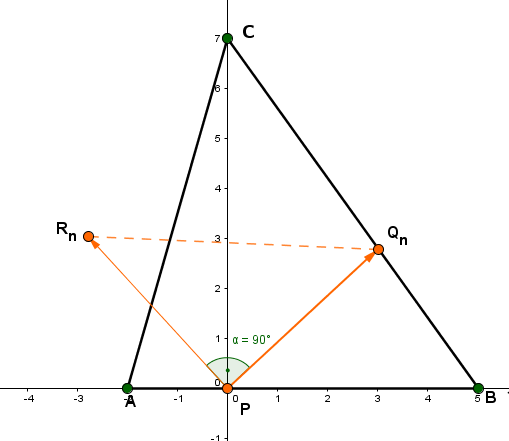
Gegeben ist das Dreieck mit den Eckpunkten und .Die Eckpunkte auf der Seite des Dreiecks bilden mit dem Punkt und Punkten auf gleichschenklig-rechtwinklige Dreiecke mit .
- 7
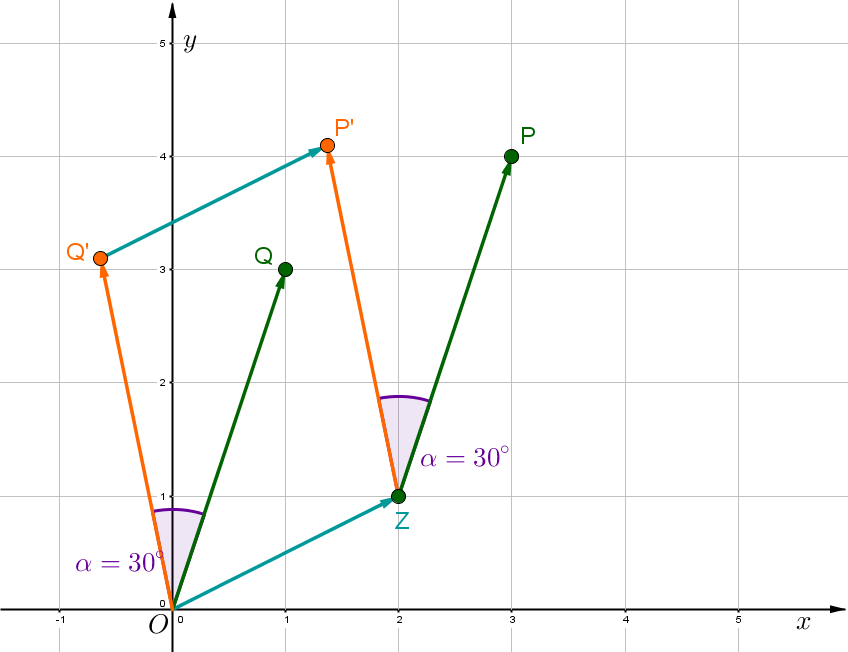
Bestimme den Punkt , den du durch eine Drehung des Punktes um das Zentrum mit dem Winkel erhältst.
, ,
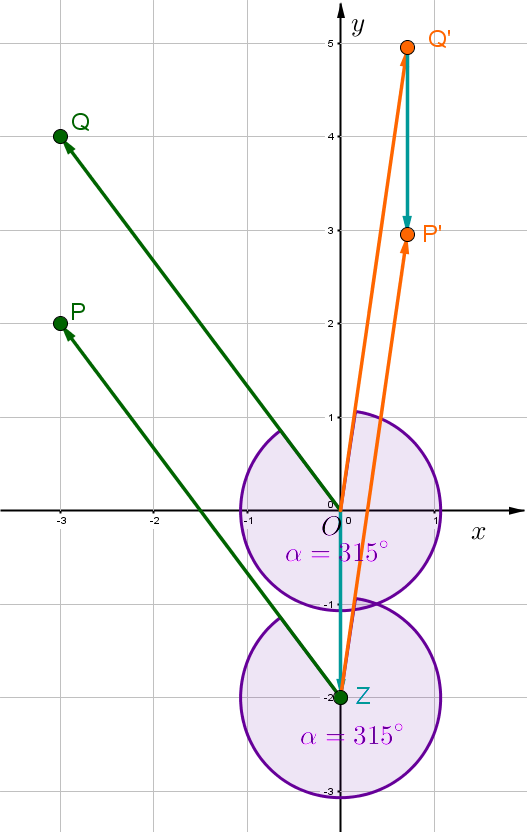
, ,
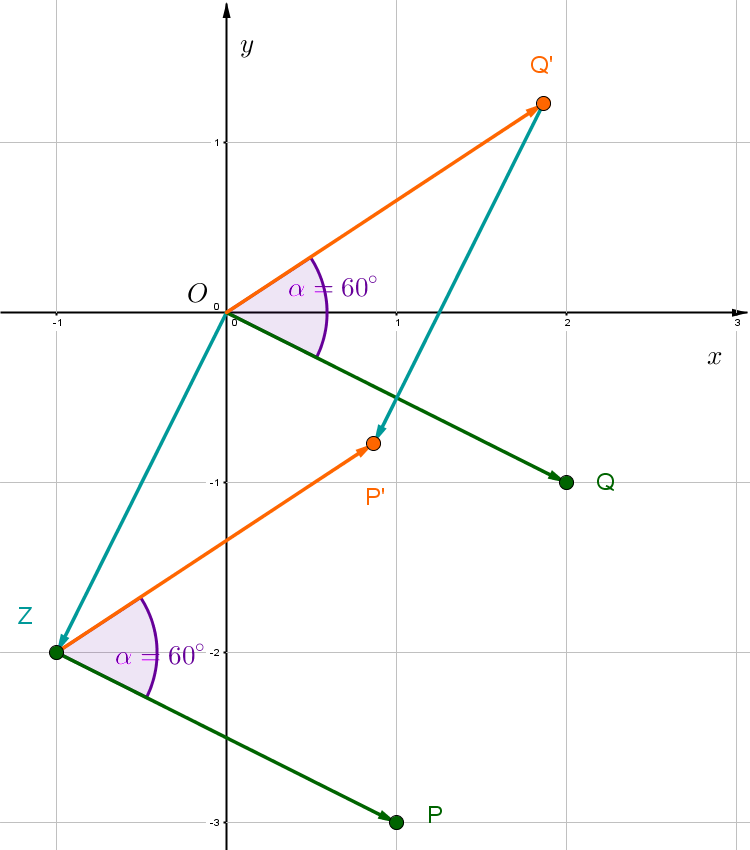
, ,
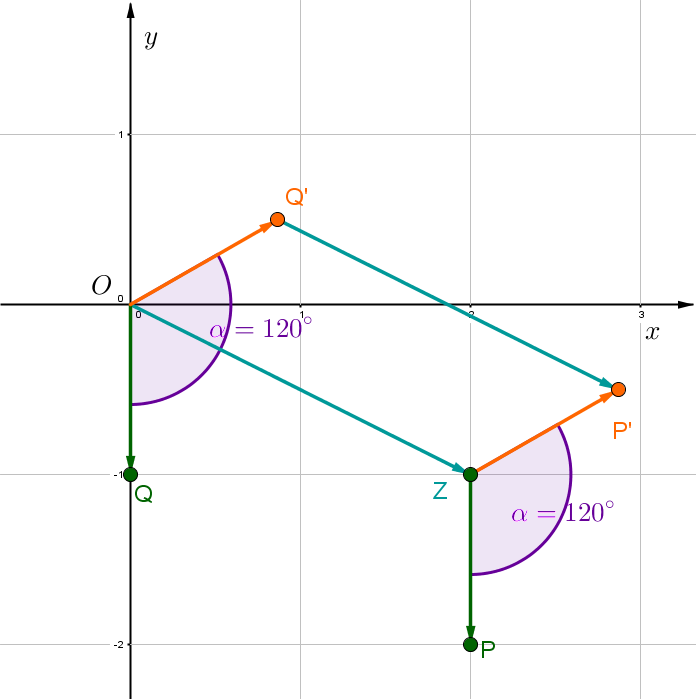
, ,
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?