Aufgaben zur Drehung - lernen mit Serlo!

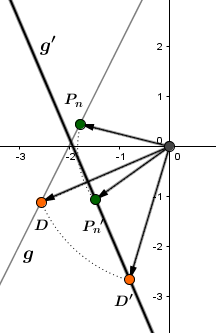
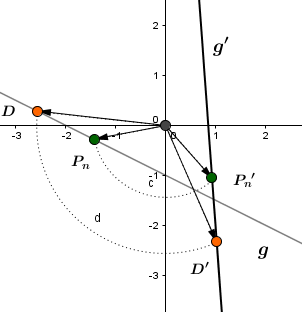
Die Gerade $g$ wird durch Drehung um den Ursprung mit dem Winkelmaß $α$ auf die Gerade $g^{'}$ abgebildet. Berechne die Geradengleichung von $g^{'}$ .

$g : y = 2 x + 4$ mit $α = 50 °$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade
Skizze:
Die Gerade $g$ mit $y = 2 x + 4$ soll mit dem Winkel $α = 50 °$ um den Ursprung gedreht werden.
Gesucht ist jetzt also die Geradengleichung von $g^{'}$ .
Man wählt einen allgemeinen Punkt $P_{n} (x | 2 x + 4)$ auf der Geraden und dreht diesen um $50 °$ um den Ursprung:
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{matrix} \cos 50 ° - \sin 50 ° \\ \sin 50 ° \cos 50 ° \end{matrix}) \cdot (\begin{matrix} x \\ 2 x + 4 \end{matrix}) =$
$(\begin{matrix} 0,6 - 0,8 \\ 0,8 0,6 \end{matrix}) \cdot (\begin{matrix} x \\ 2 x + 4 \end{matrix}) =$
$(\begin{array}{c} 0,6 x - 0,8 (2 x + 4) \\ 0,8 x + 0,6 (2 x + 4) \end{array}) =$
$(\begin{array}{c} - x - 3,2 \\ 2 x + 2,4 \end{array})$
$\Rightarrow \begin{array}{rrcc} x^{'} & = - x & - 3,2 & (1) \\ y^{'} & = 2 x & + 2,4 & (2) \end{array}$
$\Rightarrow P_{n}^{'} (- x - 3,2 | 2 x + 2,4)$
Als letztes muss noch der Trägergraph $g^{'}$ bestimmt werden:
Dazu löst man die (1)-Gleichung nach $x$ auf.
$x = - x^{'} - 3,2$
Setze (1') in (2) ein:
$y^{'} = 2 \cdot (- x^{'} - 3,2) + 2,4 = - 2 x^{'} - 6,4 + 2,4 = - 2 x^{'} - 4$
Die gedrehte Gerade hat demnach folgende Gleichung $y^{'} = - 2 x^{'} - 4$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$g : y = x - 3$ mit $α = - 30 °$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade
$g : y = x - 3$ , $α = - 30 °$
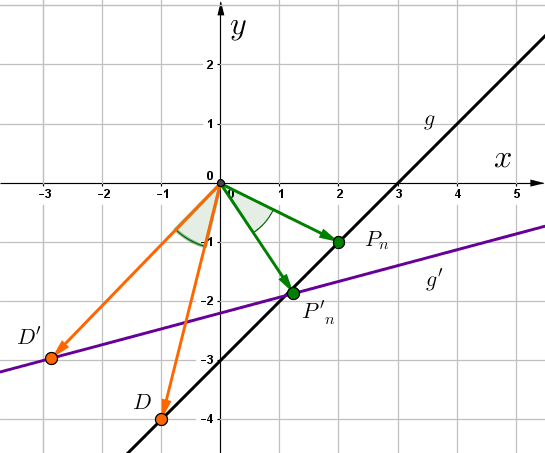
Wähle einen beliebigen Punkt auf der Gerade.
$P_{n} (x | x - 3)$
Nun spiegelst du diesen Punkt $P_{n}$ an der Geraden $g$ auf den Bildpunkt $P_{n}^{'}$ .
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} \cos α & - \sin α \\ \sin α & \cos α \end{array}) \cdot (\begin{array}{c} x \\ y \end{array})$
Setze den allgemeinen Punkt $P_{n}$ und den Winkel $α$ in die Gleichung ein.
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} \cos (- 30 °) & - \sin (- 30 °) \\ \sin (- 30 °) & \cos (- 30 °) \end{array}) \cdot (\begin{array}{c} x \\ x - 3 \end{array}) = (\begin{array}{cc} \frac{\sqrt{3}}{2} & \frac{1}{2} \\ - \frac{1}{2} & \frac{\sqrt{3}}{2} \end{array}) \cdot (\begin{array}{c} x \\ x - 3 \end{array})$
Führe die Matrix-Vektor-Multiplikation durch.
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{c} \frac{\sqrt{3}}{2} \cdot x + \frac{1}{2} \cdot (x - 3) \\ - \frac{1}{2} \cdot x + \frac{\sqrt{3}}{2} \cdot (x - 3) \end{array}) = (\begin{array}{c} \frac{1 + \sqrt{3}}{2} \cdot x - \frac{3}{2} \\ \frac{- 1 + \sqrt{3}}{2} \cdot x - \frac{3 \sqrt{3}}{2} \end{array})$
$\Rightarrow P_{n}^{'} (\frac{1 + \sqrt{3}}{2} \cdot x - \frac{3}{2} | \frac{- 1 + \sqrt{3}}{2} \cdot x - \frac{3 \sqrt{3}}{2})$
$P_{n}^{'}$ ist ein beliebiger Punkt auf der Bildgeraden.
Bestimme nun den Trägergraph $g^{'}$ .
$\begin{matrix} x^{'} & = & \frac{1 + \sqrt{3}}{2} \cdot x & - & \frac{3}{2} \\ y^{'} & = & \frac{- 1 + \sqrt{3}}{2} \cdot x & - & \frac{3 \sqrt{3}}{2} \end{matrix}$
Löse die erste Gleichung nach $x^{'}$ auf und setze diese in die zweite Gleichung ein.
$x = \frac{2 \cdot x^{'}}{1 + \sqrt{3}} - \frac{3}{1 + \sqrt{3}}$
$y^{'} = \frac{- 1 + \sqrt{3}}{2} \cdot (\frac{2 \cdot x^{'}}{1 + \sqrt{3}} - \frac{3}{1 + \sqrt{3}}) - \frac{3}{2} = \frac{\sqrt{3} - 1}{2} \cdot x^{'} - \frac{9 + 3 \sqrt{3}}{4}$
Die gespiegelte Gerade $g^{'} : y^{'} = \frac{\sqrt{3} - 1}{2} \cdot x^{'} - \frac{9 + 3 \sqrt{3}}{4}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$g : y = - 0,5 x - 1$ mit $α = 120 °$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade
Die Gerade $g$ mit $y = - 0,5 x - 1$ soll mit dem Winkel $α = 120 °$ um den Ursprung gedreht werden.
Gesucht ist jetzt also die Geradengleichung von $g^{'}$ .
Man wählt einen allgemeinen Punkt $P_{n} (x | - 0,5 x - 1)$ auf der Geraden und dreht diesen um $120 °$ um den Ursprung:
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{matrix} \cos 120 ° - \sin 120 ° \\ \sin 120 ° \cos 120 ° \end{matrix}) \cdot (\begin{matrix} x \\ - 0,5 x - 1 \end{matrix}) =$
$(\begin{matrix} - \frac{1}{2} - \frac{\sqrt{3}}{2} \\ \frac{\sqrt{3}}{2} - \frac{1}{2} \end{matrix}) \cdot (\begin{matrix} x \\ - 0,5 x - 1 \end{matrix}) =$
$(\begin{array}{c} - \frac{1}{2} x + \frac{\sqrt{3}}{4} x + \frac{\sqrt{3}}{2} \\ \frac{\sqrt{3}}{2} x + \frac{1}{4} x + \frac{1}{2} \end{array}) =$
$(\begin{array}{c} \frac{\sqrt{3} - 2}{4} x + \frac{\sqrt{3}}{2} \\ \frac{\sqrt{3} + 2}{4} x + \frac{1}{2} \end{array})$
$\Rightarrow \begin{array}{rrcc} x^{'} & = \frac{\sqrt{3} - 2}{4} x & + \frac{\sqrt{3}}{2} & (1) \\ y^{'} & = \frac{\sqrt{3} + 2}{4} x & + \frac{1}{2} & (2) \end{array}$
$\Rightarrow P_{n}^{'} (\frac{\sqrt{3} - 2}{4} x + \frac{\sqrt{3}}{2} | \frac{\sqrt{3} + 2}{4} x + \frac{1}{2})$
Als letztes muss noch der Trägergraph $g^{'}$ bestimmt werden:
Dazu löst man die (1)-Gleichung nach $x$ auf.
$x = \frac{4 (x^{'} - \frac{\sqrt{3}}{2})}{\sqrt{3} - 2}$
Setze (1') in (2) ein:
$y^{'} = \frac{\sqrt{3} + 2}{4} \cdot \frac{4 (x^{'} - \frac{\sqrt{3}}{2})}{\sqrt{3} - 2} + \frac{1}{2} = (7 + 4 \sqrt{3}) x^{'} - 12 - \frac{13}{2} \sqrt{3}$
Die gedrehte Gerade hat demnach folgende Gleichung $y^{'} = (7 + 4 \sqrt{3}) x^{'} - 12 - \frac{13}{2} \sqrt{3}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?