1 Übersicht
Ziel dieses Kurses ist es, einen Überblick über das Thema "Potenzfunktionen mit natürlichen Exponenten" zu geben.
Inhalte
Hinführung zum Begriff der Potenzfunktion
Eigenschaften einer Potenzfunktion (Steigungsverhalten, Wertemenge, Symmetrieverhalten)
Graph einer Potenzfunktion
2 Potenzfunktion (1|4)
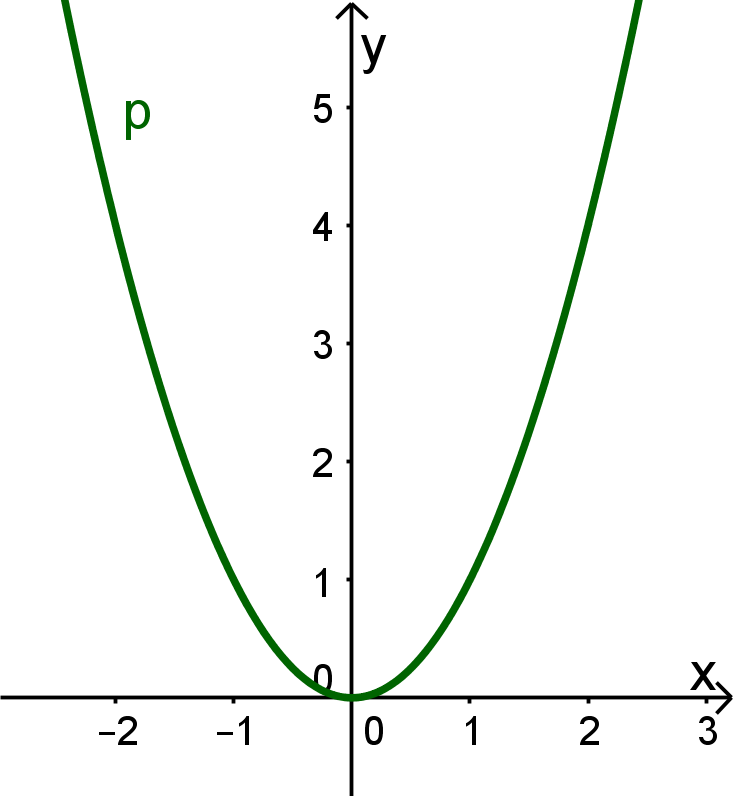
Quadratische Funktionen und Parabeln sind dir schon aus früheren Jahrgangsstufen bekannt.
Rechts siehst du zum Beispiel den Graphen der Funktion , auch Normalparabel genannt.
Natürlich können wir aber nicht nur das Quadrat von betrachten, sondern auch höhere Potenzen, zum Beispiel , untersuchen. Es ergibt sich also die Frage:
3 Potenzfunktion (2|4)
Wie du unten erkennen kannst, sehen die Graphen von und recht ähnlich aus, wobei der Graph von etwas gestauchter und "U-förmiger" aussieht. Beide Graphen sind aber achsensymmetrisch und auf beiden Seiten nach gerichtet.

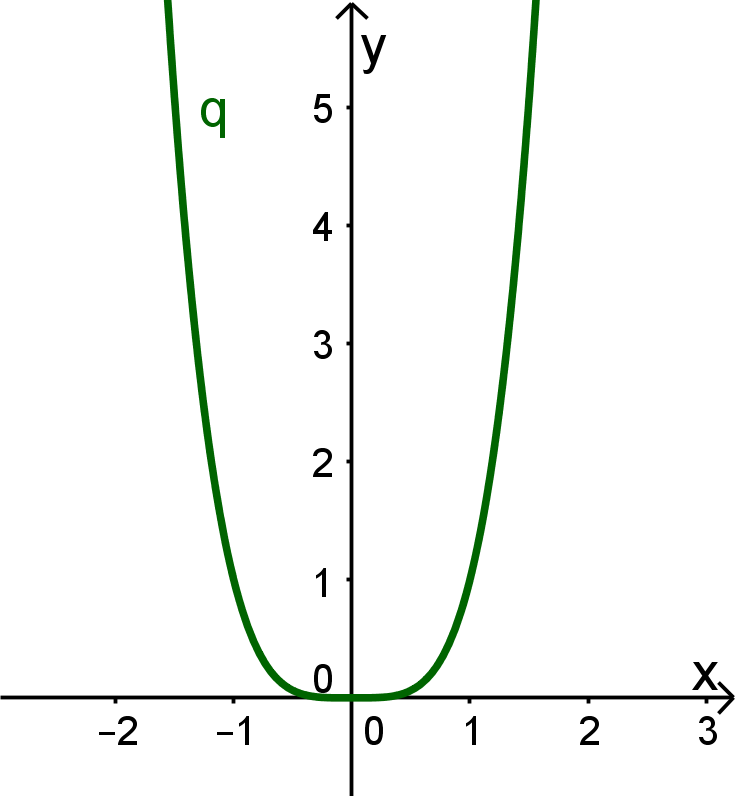
Was vermutest du für den Graphen von ?
Wird der Graph von vielleicht zwischen den Graphen von und verlaufen? Oder ganz anders ausschauen? Was passiert für negative -Werte?
Denke nach, und gehe dann zur nächsten Seite dieses Kurses …
4 Potenzfunktion (3|4)
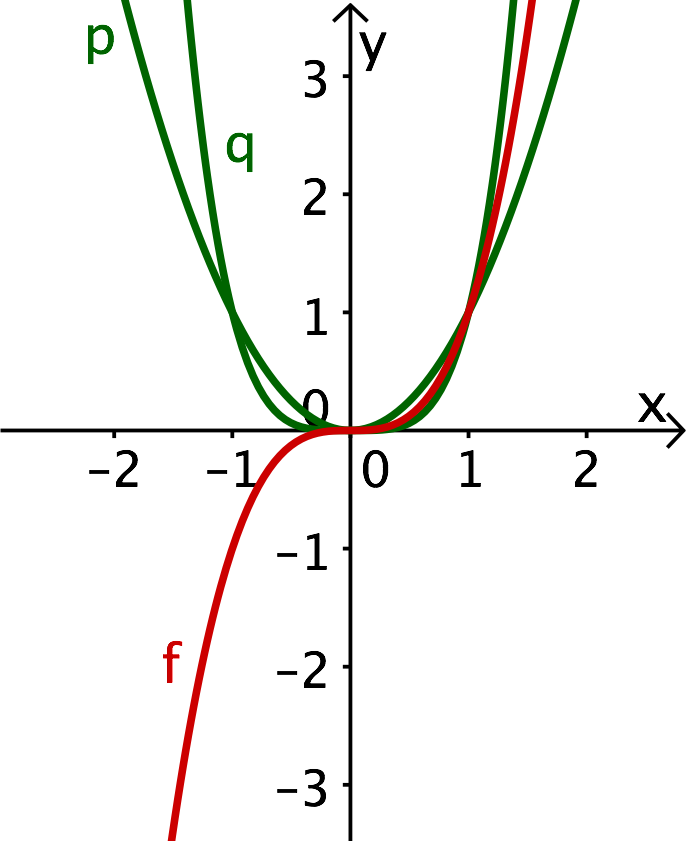
Rechts ist zusätzlich zu den Funktionen und nun auch die Funktion in Rot eingezeichnet.
Und war deine Vermutung richtig?
Wie du siehst, unterscheidet sich der Graph von vor allem dadurch, dass er in negative Richtung nach läuft.
Für positive -Werte verläuft der Graph tatsächlich zwischen und .
Warum läuft ins Negative?
Bei wird der -Wert dreimal mit sich selbst multipliziert. Bei negativen -Werten erhält man somit ein negatives Ergebnis.
Für und gilt zum Beispiel:
Ähnlich sieht es bei also allgemein bei Potenzen mit ungeradem Exponenten aus.
Damit ist der Graph nicht mehr achsensymmetrisch zur -Achse, sondern punktsymmetrisch zum Ursprung.
5 Potenzfunktion (4|4)
An dieser Stelle ist es sinnvoll, einen Begriff für Funktionen wie einzuführen:
Die Form der Potenzfunktion hängt vom Exponenten und Koeffizienten ab.
Eine gerade Potenzfunktion ist eine Potenzfunktion mit geradem Exponenten wie .
Eine ungerade Potenzfunktion ist eine Potenzfunktion mit ungeradem Exponenten wie .
Den Exponenten in einer Potenzfunktion kann man auch Grad nennen.
Dabei kann eine Potenzfunktion auch den Grad haben. In diesem Fall handelt es sich um eine konstante Funktion. So ist zum Beispiel auch eine Potenzfunktion.
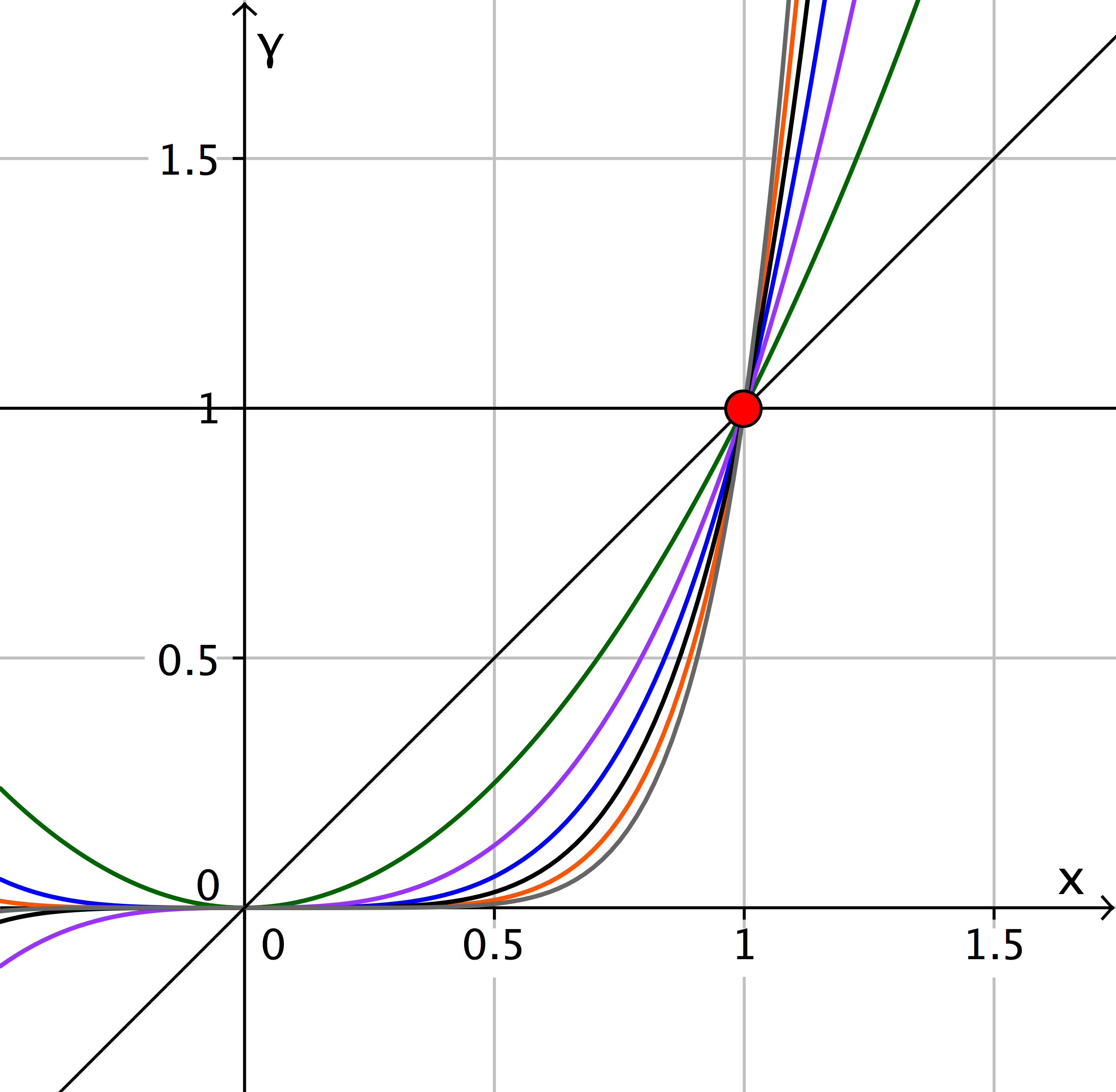
Rechts findest du die Graphen von .
Beim Untersuchen der Graphen fällt dir bestimmt auf, dass sie sich alle in dem Punkt schneiden (hier rot eingezeichnet).
Werden diese Potenzfunktionen mit einem Koeffizienten multipliziert, z. B. , so verändert sich dieser "Fixpunkt" ebenso. Er hätte nun z.B. die Koordinaten .
Auf der nächsten Kursseite kannst du mithilfe von Applets herausfinden, welchen Einfluss der Koeffizient und der Exponent auf den Verlauf des Graphen haben.
6 Graphen gerader Potenzfunktionen
Graph einer Potenzfunktion
In den Applets auf den nächsten zwei Seiten siehst du, wie die Veränderung des Exponenten und des Koeffizienten sich auf den Graphen der Potenzfunktion auswirken.
Benutze dabei die Schieberegler, um den Koeffizienten und den Exponenten zu variieren.
Potenzfunktion mit geradem Exponenten
Was fällt dir auf beim Verändern des Koeffizienten beim Graphen bezüglich…
… des Steigungsverhaltens?
… der Wertemenge?
… des Symmetrieverhaltens?
7 Graphen ungerader Potenzfunktionen
Auf dieser Seite findest du das entsprechende Applet für Potenzfunktionen mit ungeradem Exponenten.
Potenzfunktion mit ungeradem Exponenten
Was fällt dir auf beim Verändern des Koeffizienten beim Graphen bezüglich…
… des Steigungsverhaltens?
… der Wertemenge?
… des Symmetrieverhaltens?
Zusammenfassung
Gerade Potenzfunktion | Ungerade Potenzfunktion | |
|---|---|---|
Steigungsverhalten | : Graph ist nach oben geöffnet : Graph ist nach unten geöffnet | : Graph steigt überall : Graph fällt überall |
Wertemenge | bei bei | |
Symmetrieverhalten | achsensymmetrisch zur -Achse | punktsymmetrisch zum Ursprung |
8 Aufgaben zu Graphen von Potenzfunktionen
Aufgabe 1
Laden
Aufgabe 2
Bestimme die Symmetrie und den Verlauf der Graphen folgender Potenzfunktionen und gib jeweils die Wertemenge und den Grad an.
Laden
Laden
Laden
Feedback
Damit wir unseren Kurs für die Zukunft verbessern können, würden wir uns sehr über ein Feedback von dir freuen. Es dauert auch nur 3 Minuten!
Klicke dazu auf diesen Link.
