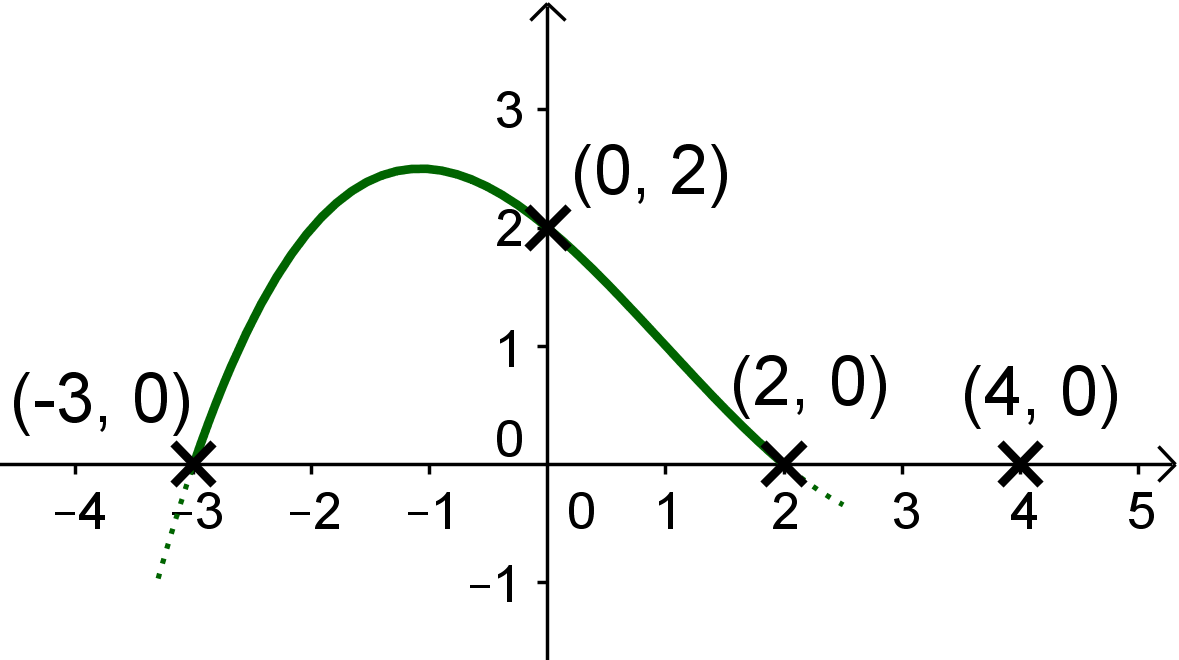
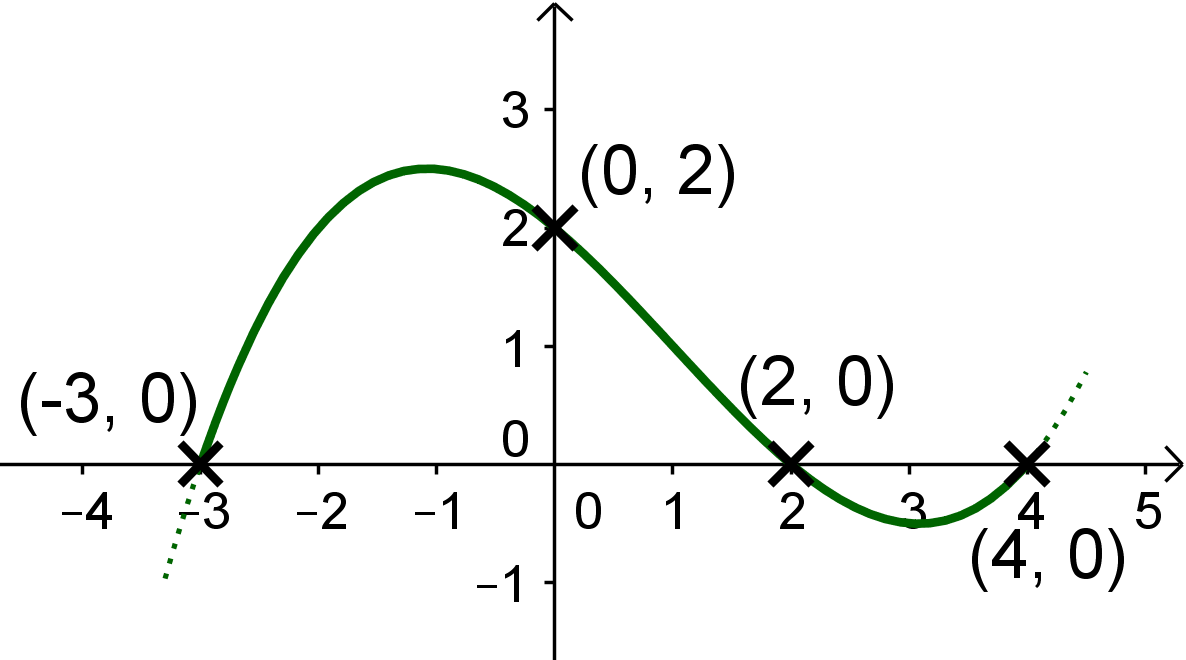
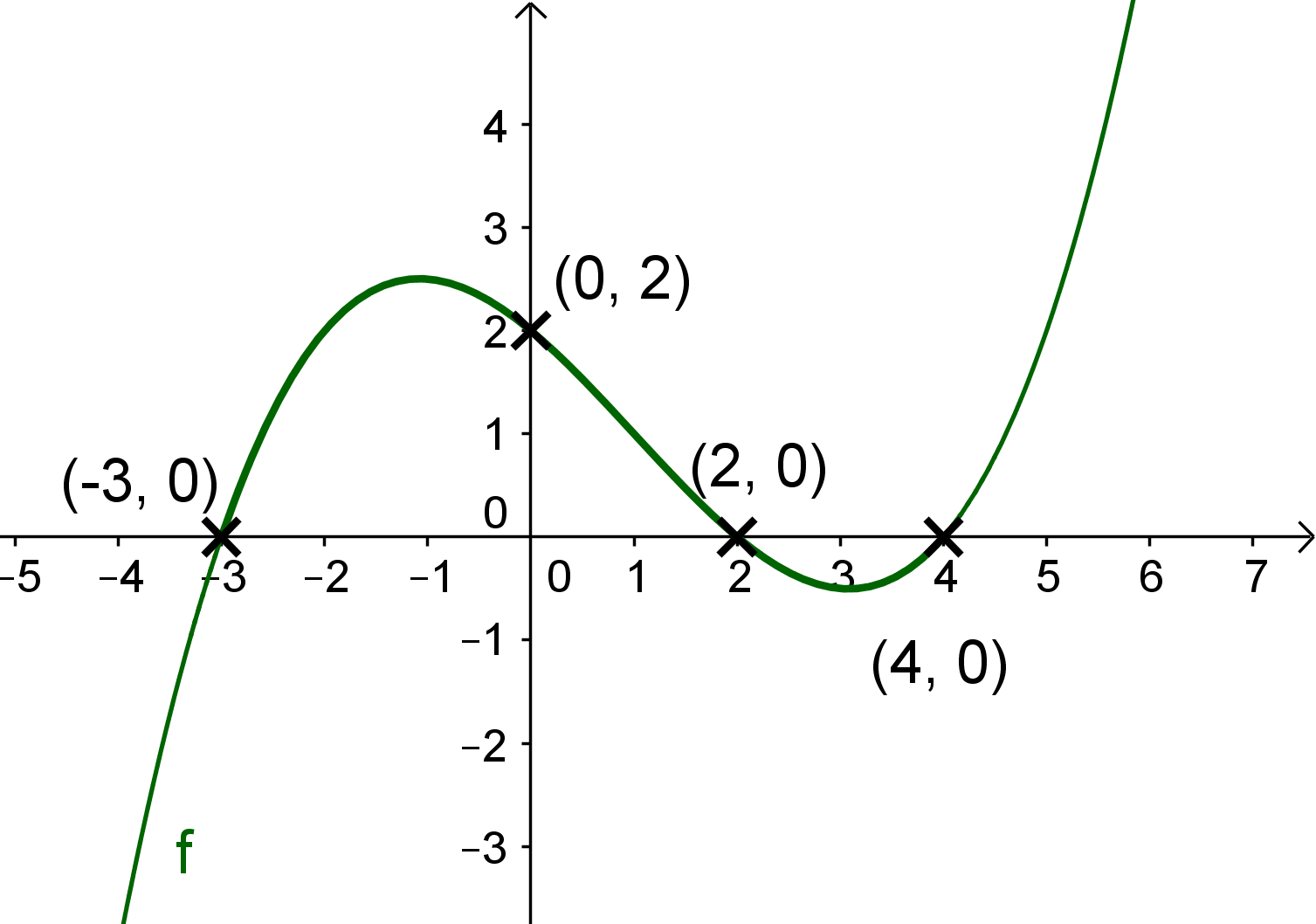
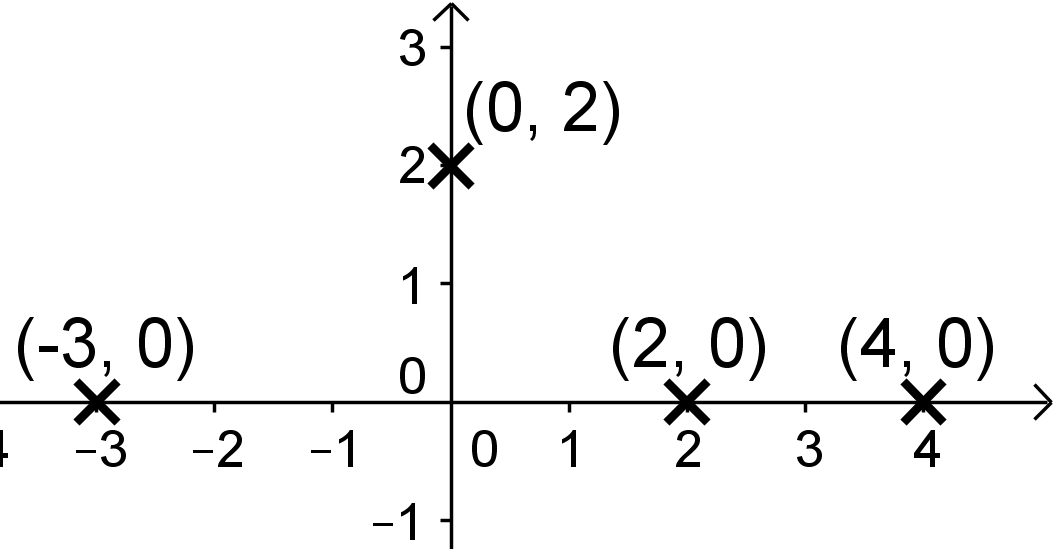Skizziere mit Hilfe den gegebenen Informationen jeweils einen möglichen Verlaufdes Graphen der folgenden Funktionen.
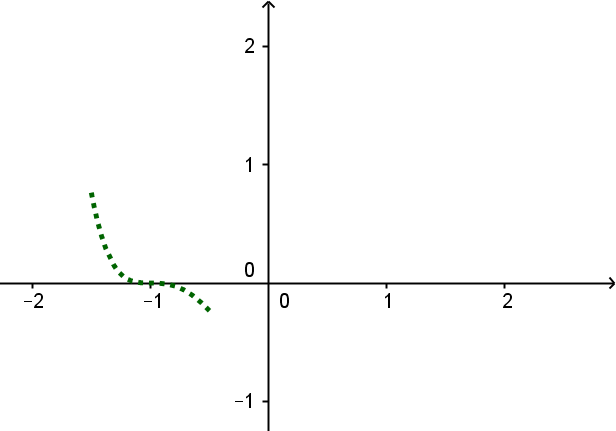
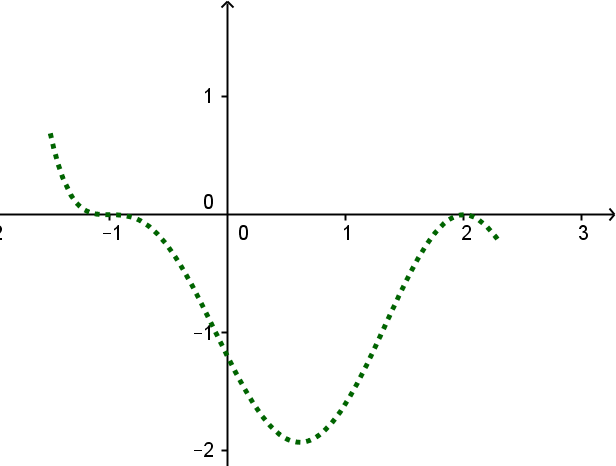
Die Polynomfunktion vom Grad besitzt Nullstellen bei , und und schneidet die -Achse im Punkt .
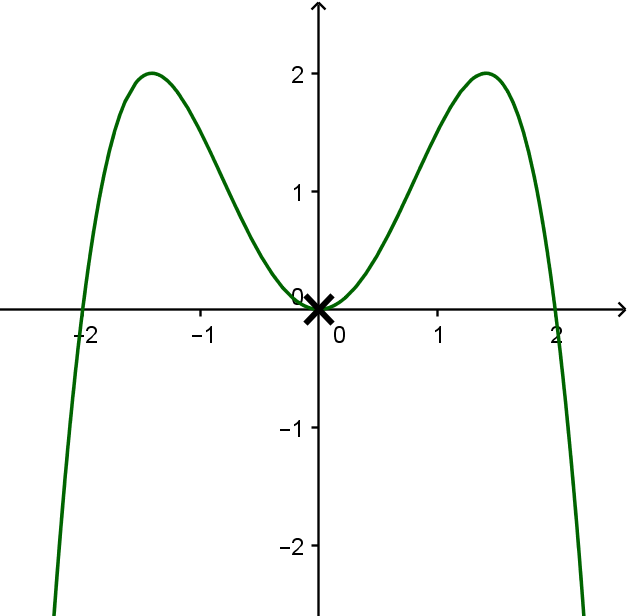
Die Polynomfunktion vom Grad hat genau eine doppelte Nullstelle und ihr Graph ist symmetrisch zur -Achse.
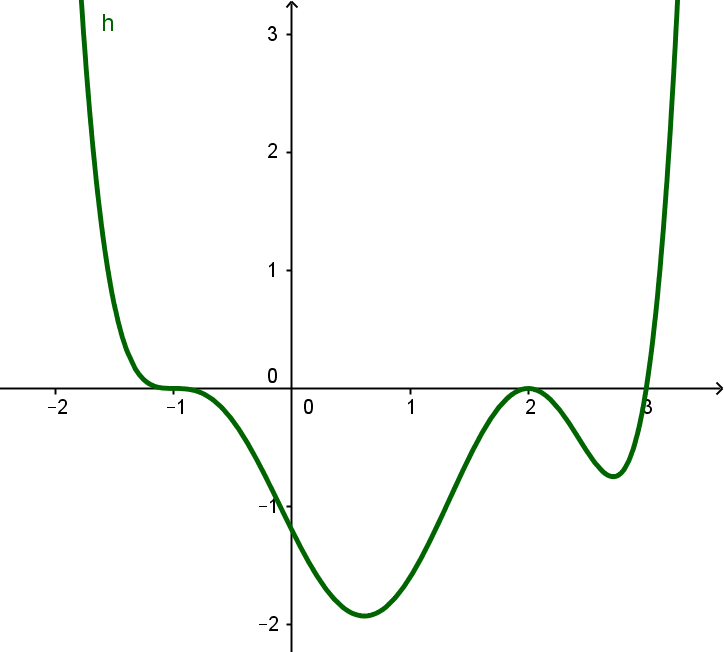
Die Polynomfunktion vom Grad besitzt zwei mehrfache Nullstellen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?