Aufgaben zur Nullstelle
Hier findest du Übungsaufgaben rund um das Thema Nullstelle. Lies sie ab, berechne sie und leite aus ihnen weitere Aussagen ab.
- 1
Lies die Nullstelle(n) folgender Funktionen ab

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Hier wird die Nullstelle erst graphisch und dann rechnerisch bestimmt.
Man sieht, dass der Graph der Funktion die x-Achse genau im Punkt (4|0) schneidet.
Nullstelle bei .
Graphische Veranschaulichung:
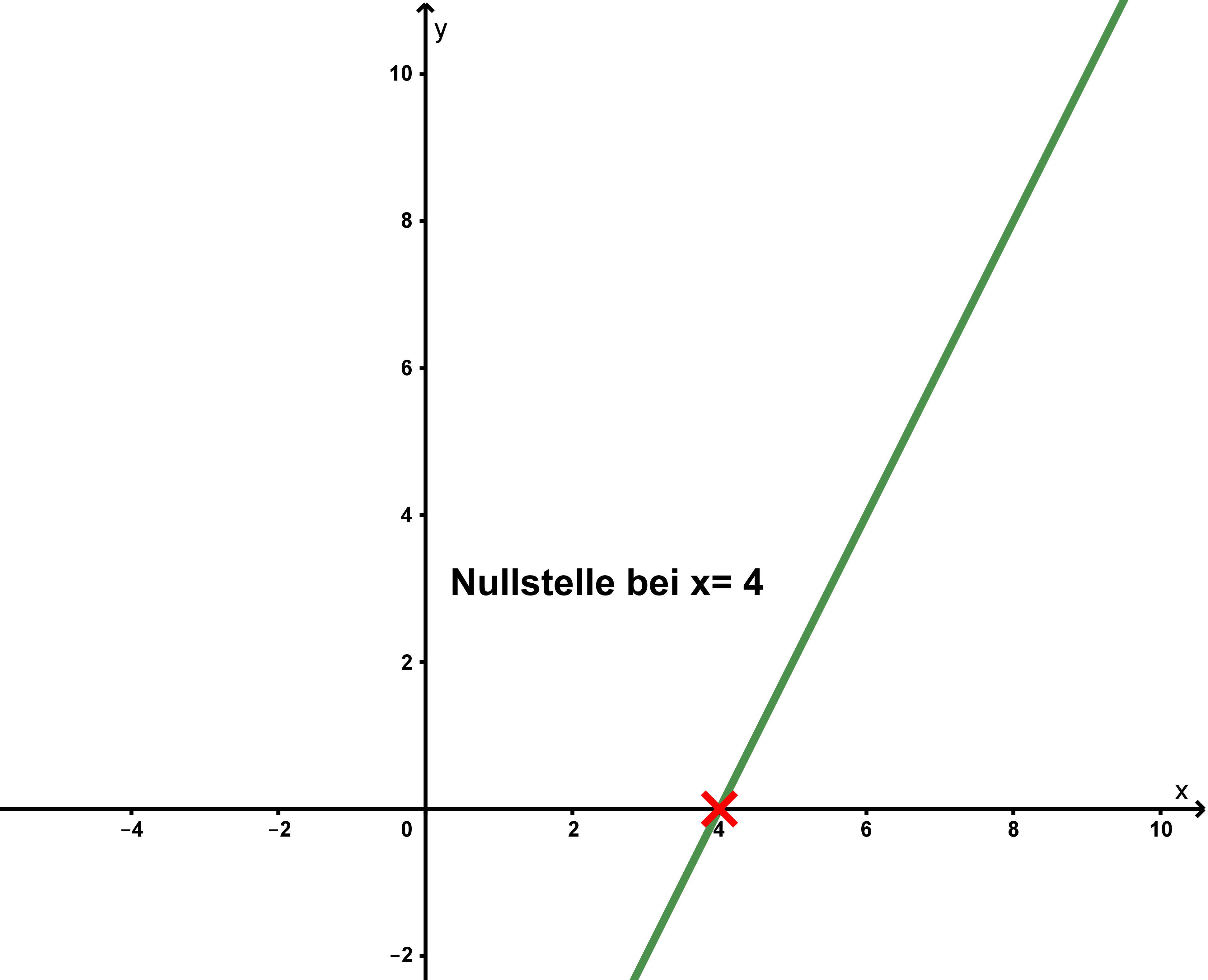
Lösung durch Berechnung:
↓ Setze
Die Nullstelle der Funktion liegt bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Hier werden die Nullstellen erst graphisch und dann rechnerisch bestimmt.
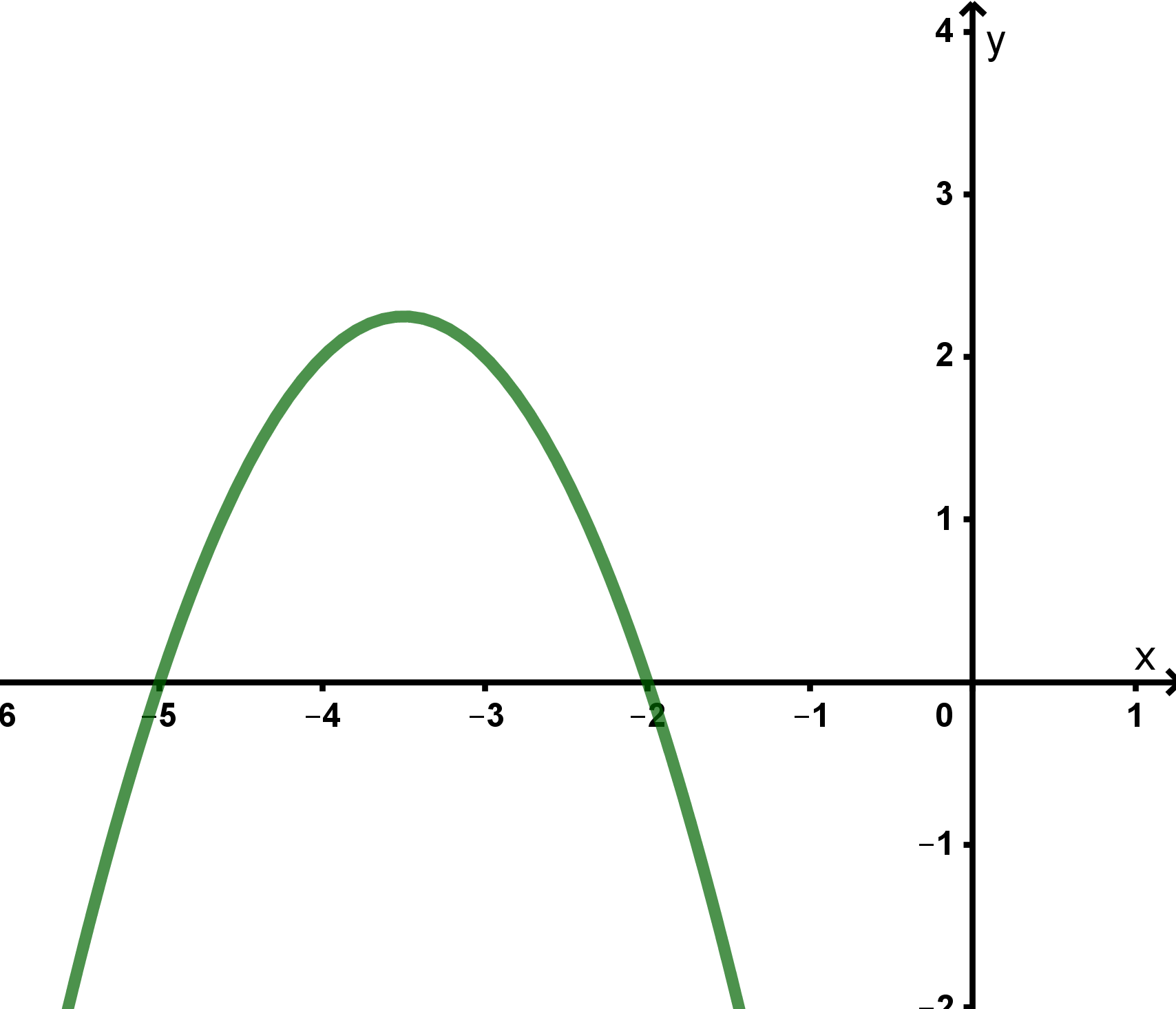
Man sieht, dass der Graph der Funktion f die x-Achse genau in den Punkten (-5|0) und (-2|0) schneidet.
⇒ Nullstellen bei und
Graphische Veranschaulichung:
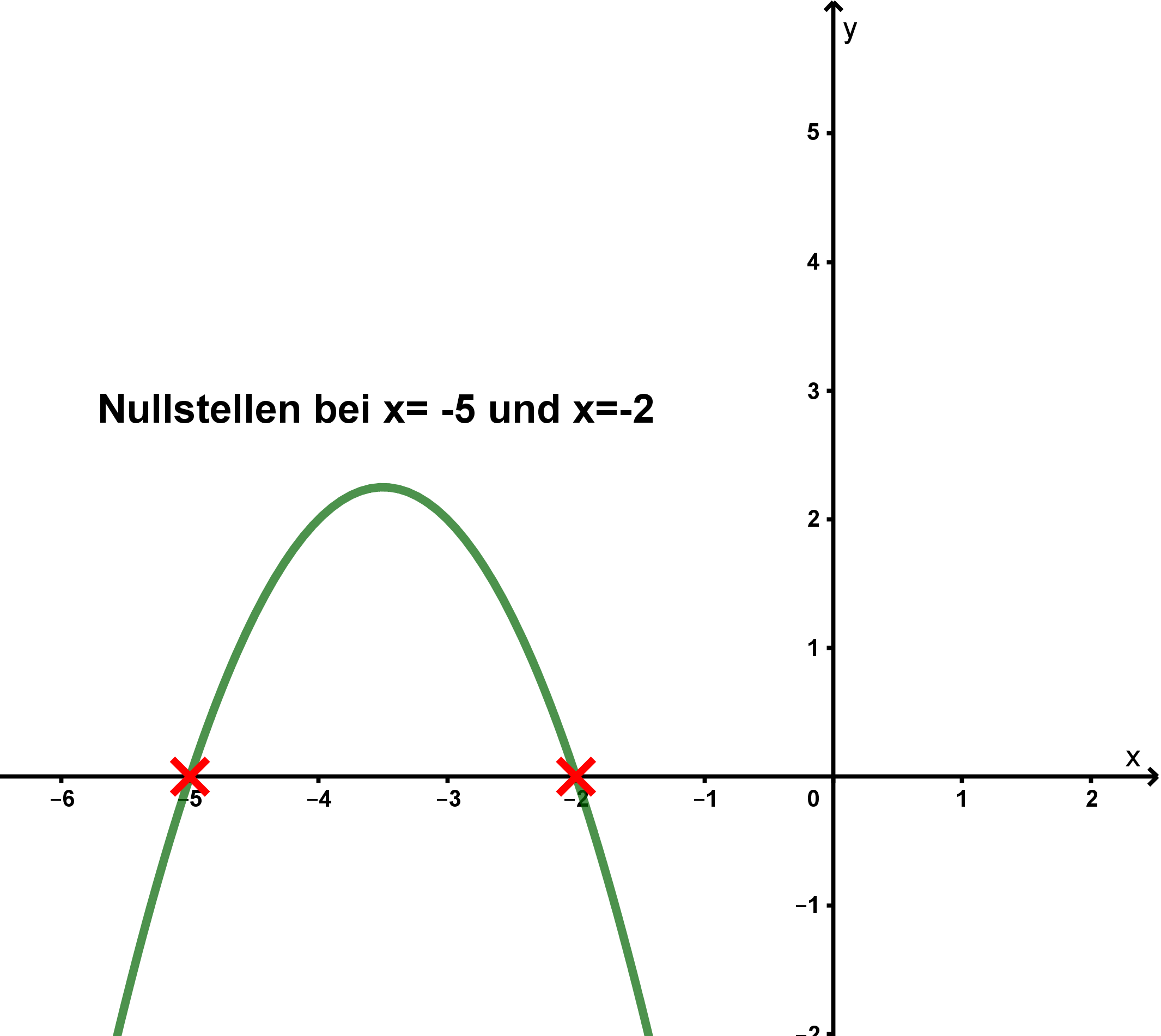
Lösung durch Berechnung:
↓ Setze
↓ Wende die Mitternachtsformel an.
↓ Multipliziere die Klammern aus.
↓ Berechne die Wurzel
↓ 1 Fall:
↓ 2 Fall:
Die beiden Nullstellen der Funktion liegen bei und .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Hier werden die Nullstellen erst graphisch und dann rechnerisch bestimmt.
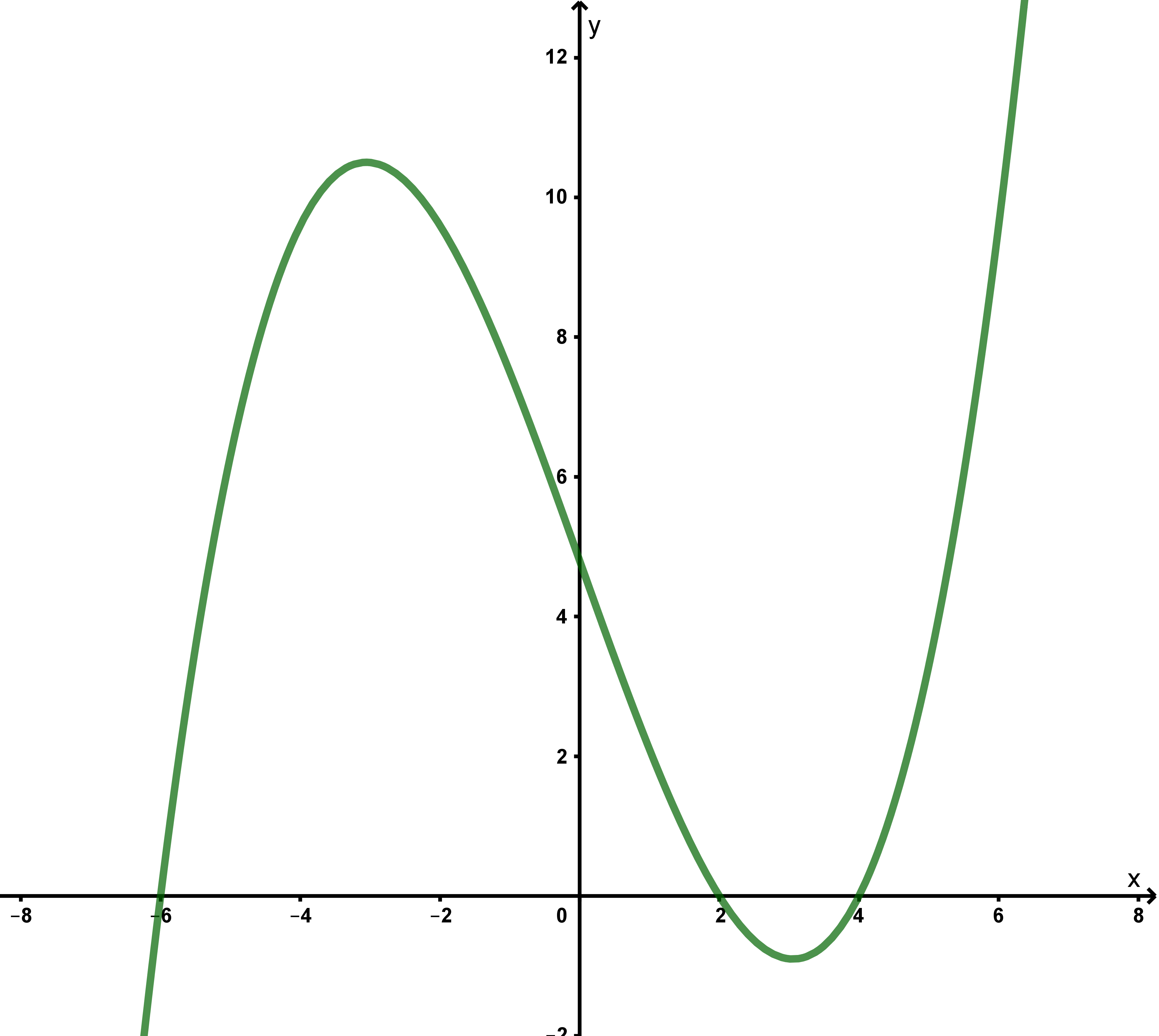
Man sieht, dass der Graph der Funktion die x-Achse genau in den Punkten (-6|0), (2|0) und (4|0) schneidet.
⇒ Nullstellen bei und und .
Graphische Veranschaulichunng

Lösung durch Berechnung:
Zur Berechnung der Nullstellen setze .
Ein Produkt aus mehreren Faktoren ist immer dann , wenn mindestens ein Faktor ist.
Für , und gilt:
Die Nullstellen der Funktion liegen bei , und .
Hast du eine Frage oder Feedback?
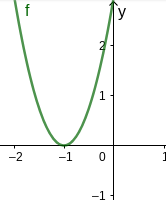
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Hier werden die Nullstellen erst graphisch und dann rechnerisch bestimmt.
Man sieht, dass der Graph der Funktion f die x-Achse genau in einem Punkt (-1|0) berührt.
⇒ Nullstelle bei x=−1.
Graphische Veranschaulichung
Lösung durch Berechnung
Zur Berechnung der Nullstellen setze .
Kürze durch 3.
Ermittle die Lösung durch die Mitternachtsformel:
Die Nullstelle liegt also bei .
Hast du eine Frage oder Feedback?
- 2
Bestimme die Vielfachheiten der Nullstelle(n) zu folgenden Funktionen
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
Zerlege in Linearfaktoren
Lies die Vielfachheit der Nullstelle am Exponenten ab.
Die Funktion hat bei eine Nullstelle der Vielfachheit 7.
Hast du eine Frage oder Feedback?
Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
Zerlege in Linearfaktoren
Lies die Vielfachheit der Nullstelle am Exponenten ab.
Die Funktion hat bei eine einfache Nullstelle.
Hast du eine Frage oder Feedback?
Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
ist bereits in der Linearfaktordarstellung. Deshalb kannst du die Vielfachheit der Nullstelle direkt am Exponenten ablesen.
Die Funktion hat bei eine doppelte Nullstelle.
Hast du eine Frage oder Feedback?
Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
Zerlege in Linearfaktoren.
Verwende die 3. binomischen Formel.
Lies aus der Linearfaktordarstellung die Vielfachheiten der Nullstellen an den Exponenten ab.
Die Funktion hat bei und jeweils eine einfache Nullstelle.
Hast du eine Frage oder Feedback?
Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
ist schon in Linearfaktordarstellung. Du kannst also die Vielfachheiten der Nullstellen direkt an den Exponenten ablesen.
Die Funktion hat bei eine einfache und bei eine doppelte Nullstelle.
Hast du eine Frage oder Feedback?
Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
- 3
Bestimme die Intervalle auf der -Achse, in denen der Graph der folgenden Funktionen oberhalb der -Achse verläuft.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Gegeben:
Gesucht: Intervalle für die
Faktorisiere zuerst . Dies geht hier mit der 3. binomischen Formel
Bestimme die Vielfachheiten der Nullstellen
Die drei Nullstellen bei sind einfache Nullstellen.
Bestimme jetzt noch das Vorzeichen in einem Bereich. Zum Beispiel in dem Bereich
Für im Intervall ist positiv, denn:
Einfache Nullstelle bei , also ist der Graph im Intervall im negativen Bereich.
Einfache Nullstelle bei , also ist der Graph im Intervall im positiven Bereich.
Einfache Nullstelle bei , also ist der Graph im Intervall im negativen Bereich.
Lösung: Der Graph verläuft in den Intervallen und oberhalb der -Achse
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Gegeben:
Gesucht: Intervalle mit
Faktorisiere zuerst den Term. Dies geht hier mit der 2. binomischen Formel .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstelle bei ist eine doppelte Nullstelle, die bei ist eine einfache.
Bestimme jetzt noch das Vorzeichen in einem Bereich. Zum Beispiel in dem Bereich .
Für im Intervall ist , denn:
Bestimme jetzt den Verlauf mithilfe der Vielfachheiten.
Weil bei eine doppelte Nullstelle ist, ändert sich da das Vorzeichen nicht.
Doppelte Nullstelle bei , also ist der Graph im Intervall ebenfalls im positiven Bereich.
Weil bei eine einfache Nullstelle ist, ändert sich dort das Vorzeichen.
Einfache Nullstelle bei , also ist der Graph im Intervall im negativen Bereich.
Lösung: Der Graph ist in den Intervallen und oberhalb der -Achse.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Gegeben:
Geuscht: Intervalle mit
Faktorisiere zuerst den Term. Dies geht hier mit der 2. binomischen Formel
Dabei ist und
Bestimme die Vielfachheiten der Nullstellen
Die Nullstelle bei ist eine einfache, die bei eine doppelte und die bei wieder eine einfache Nullstelle.
Bestimme jetzt noch das Vorzeichen in einem Bereich. Zum Beispiel in dem Bereich
Für im Intervall ist positiv, denn:
Bestimme jetzt den Verlauf mithilfe der Vielfachheiten.
Weil bei eine einfache Nullstelle ist, ändert sich dort das Vorzeichen.
Einfache Nullstelle bei , also ist der Graph im Intervall im negativen Bereich.
Weil bei eine doppelte Nullstelle ist, ändert sich dort das Vorzeichen nicht.
Doppelte Nullstelle bei , also ist der Graph im Intervall ebenfalls im negativen Bereich.
Weil bei eine einfache Nullstelle ist, ändert sich dort das Vorzeichen.
Einfache Nullstelle bei , also ist der Graph im Intervall im positiven Bereich.
Lösung: Der Graph ist in den Intervallen und im positiven Bereich.
Hast du eine Frage oder Feedback?
- 4
Skizziere mit Hilfe den gegebenen Informationen jeweils einen möglichen Verlaufdes Graphen der folgenden Funktionen.
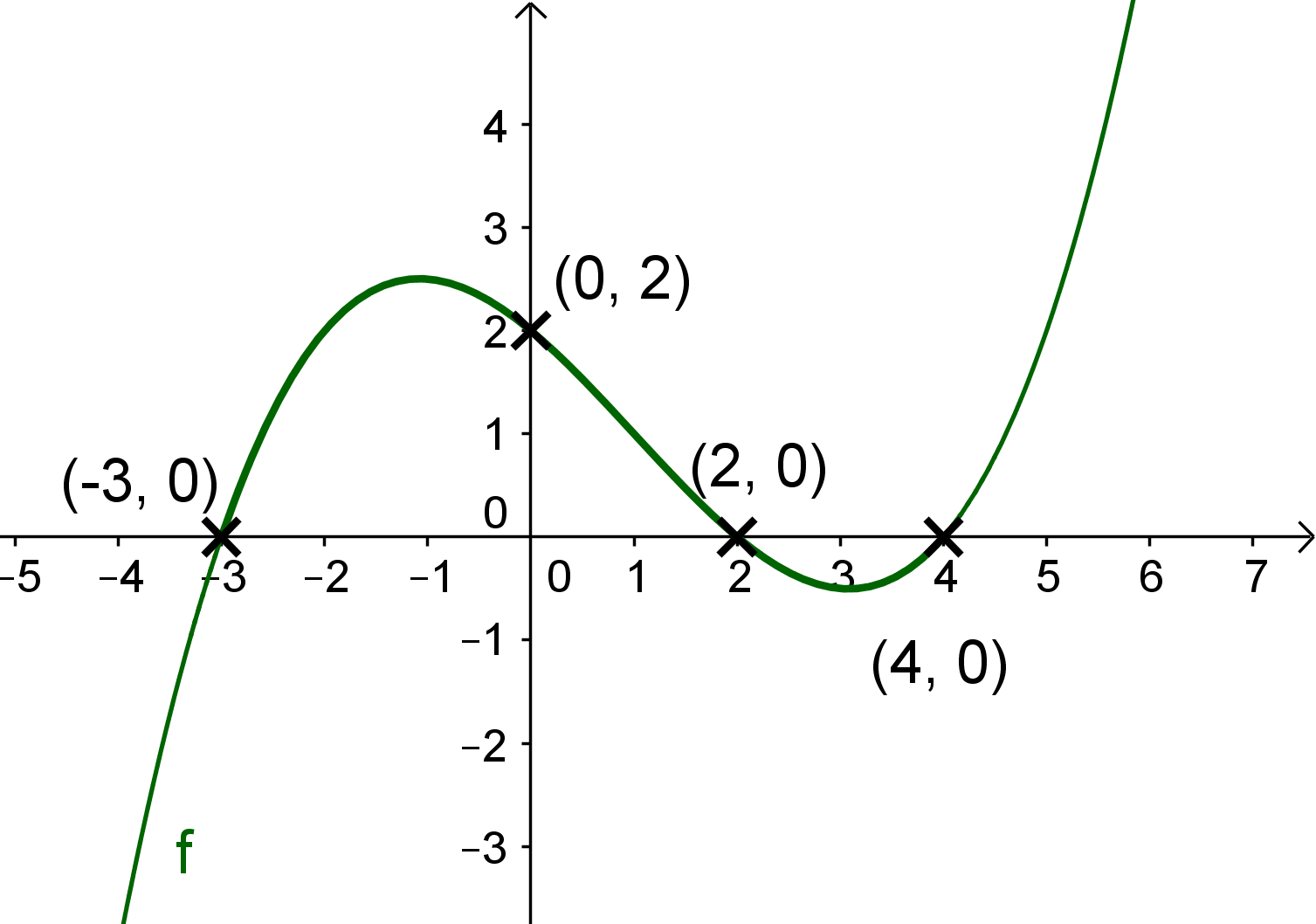
Die Polynomfunktion vom Grad besitzt Nullstellen bei , und und schneidet die -Achse im Punkt .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Gegeben:
Polynomfunktion vom Grad
Nullstellen bei und Punkt
Gesucht: Skizze von Graph
Zeichne zuerst die gegebenen Punkte in ein Koordinatensystem. Die Nullstellen liegen auf der -Achse.
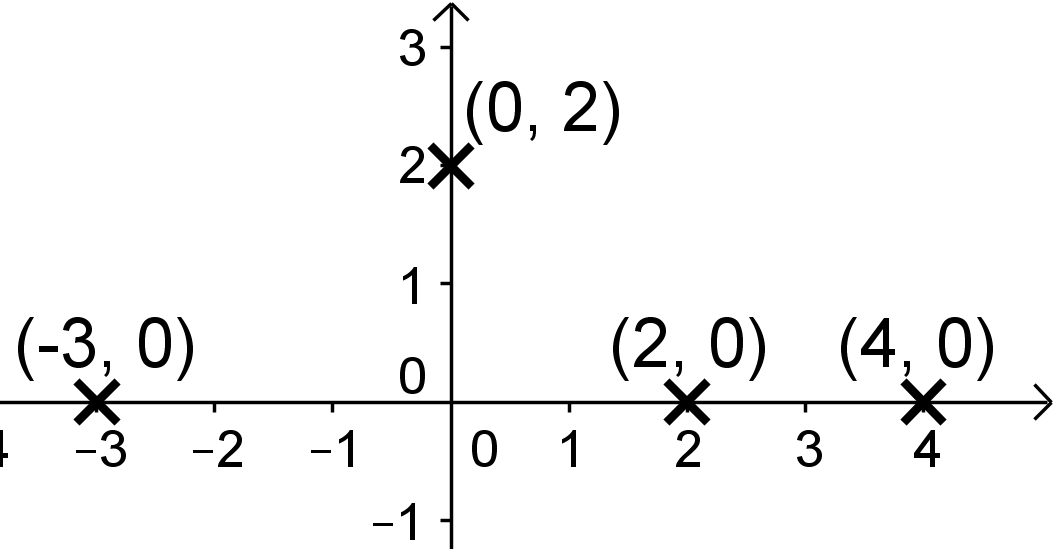
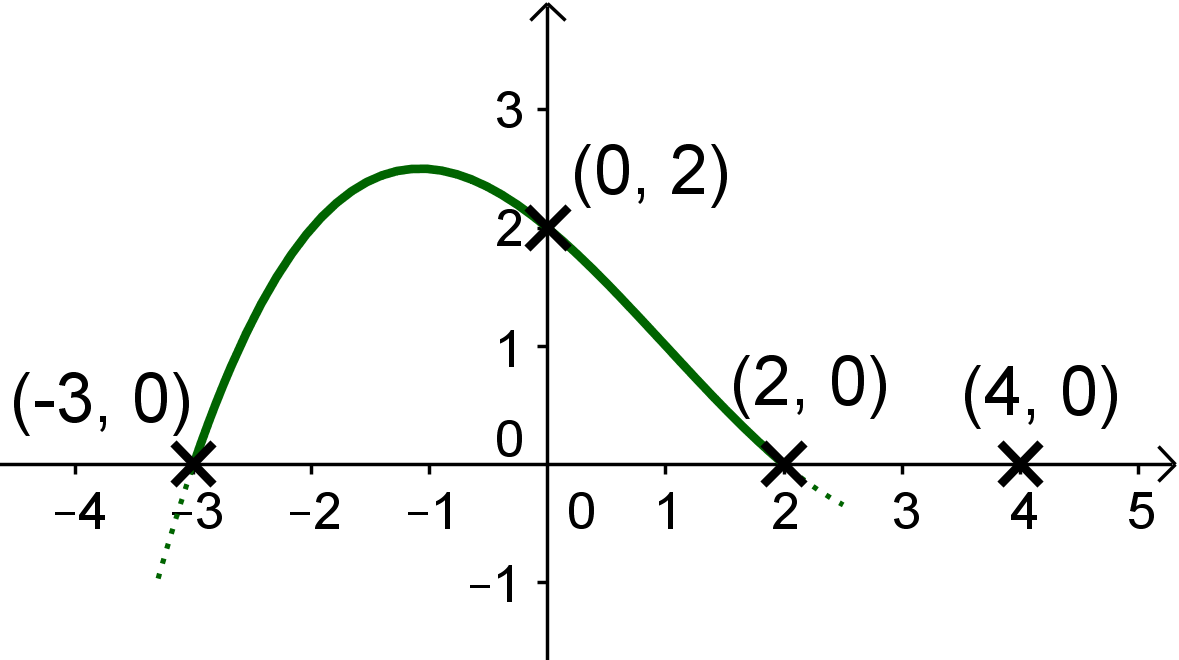
Da die Funktion vom Grad ist, kann es keine weiteren Nullstellen geben und die drei Nullstellen sind einfache Nullstellen.
Der Verlauf geht also von zu und dann zu . Wichtig ist, dass er NICHT nochmal die -Achse schneidet. Wo der Hochpunkt zwischen und genau ist, ist egal.
Zeichne als Nächstes den Graph zwischen und weiter. Dort verläuft er im negativen Bereich. Auch hier ist egal, wo der Tiefpunkt zwischen und genau ist.
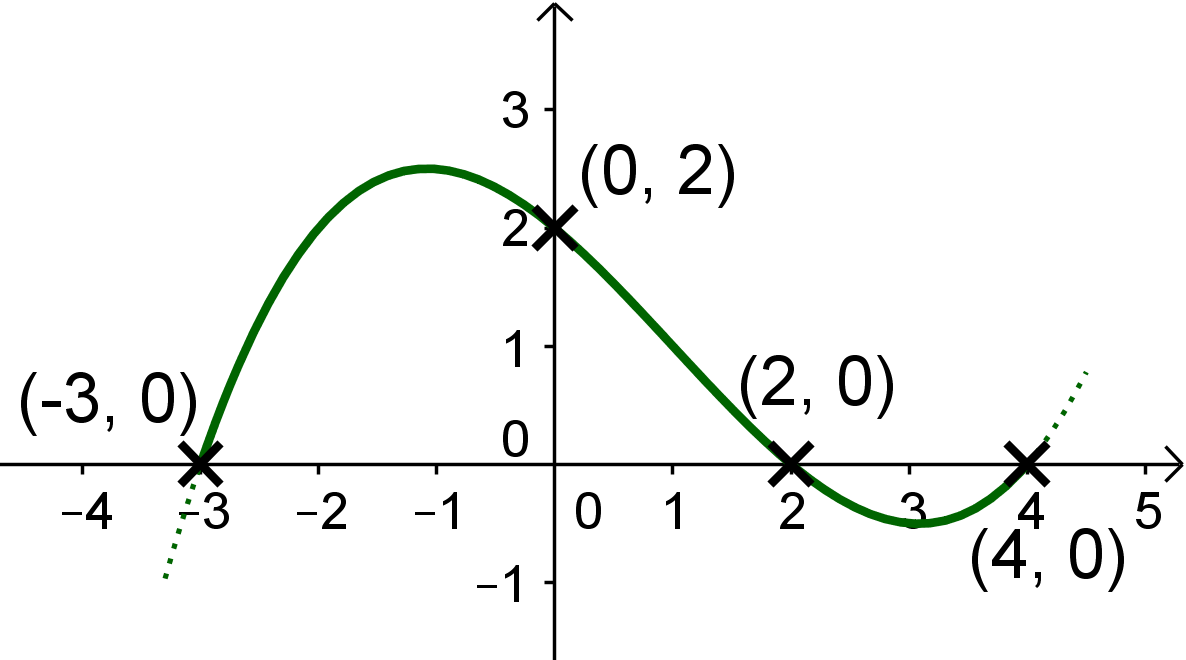
Zeichne jetzt den ganzen Graphen. Auch und sind einfache Nullstellen, also schneidet der Graph die x-Achse.
Lösung:
Hast du eine Frage oder Feedback?
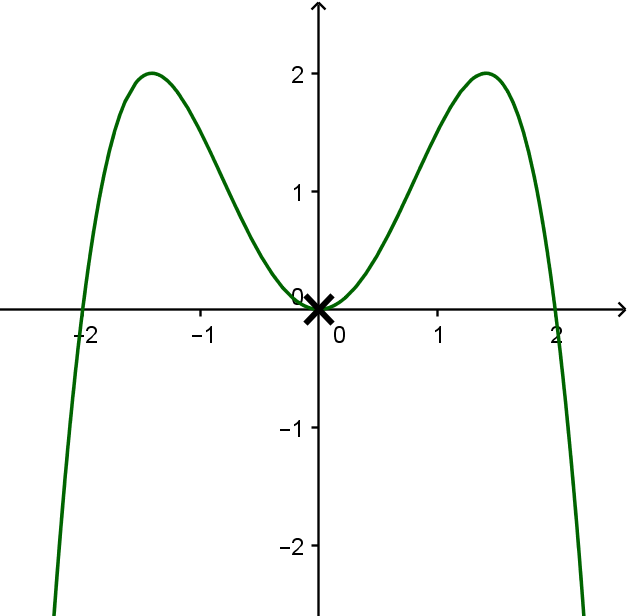
Die Polynomfunktion vom Grad hat genau eine doppelte Nullstelle und ihr Graph ist symmetrisch zur -Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Gegeben: Polynomfunktion vom Grad , genau eine doppelten Nullstelle, und der Graph symmetrisch zur -Achse
Gesucht: Skizze eines möglichen Graphen
Überlege zunächst, wo die doppelte Nullstelle hinkommt. Da der Graph symmetrisch zur -Achse ist, muss sie bei sein, denn wenn sie z.B. bei wäre, müsste durch die Symmetrie bei auch eine sein. Ob der Graph die -Achse von unten oder von oben berührt, ist beides richtig.

Zeichne jetzt den weiteren Verlauf.
Beachte dabei: Die Funktion ist vom Grad , also hat sie höchstens zwei weitere Nullstellen. Außerdem auch nur maximal Extremstellen.
Eine mögliche Lösung:
Hast du eine Frage oder Feedback?
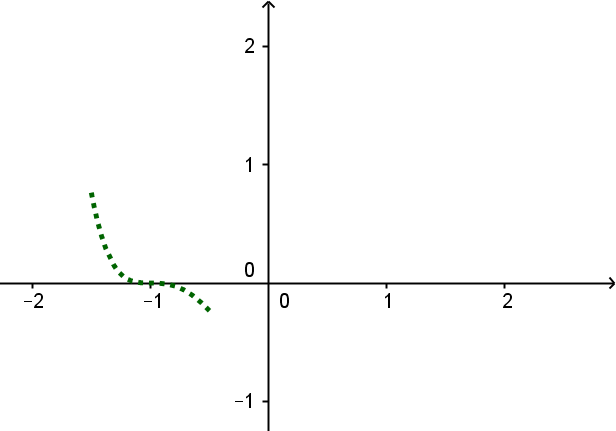
Die Polynomfunktion vom Grad besitzt zwei mehrfache Nullstellen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Gegeben: Polynomfunktion vom Grad , zwei mehrfache Nullstellen
Gesucht: Skizze von möglichem Graphen
Bei dieser Aufgabe gibt es viele verschiedene Möglichkeiten, hier wird eine -fache Nullstelle bei und eine doppelte Nullstelle bei verwendet.
Du kannst aber beispielsweise auch zwei -fache Nullstellen einzeichnen, oder zwei doppelte, oder eine doppelte und eine -fache.
Skizziere als Erstes den Verlauf der Funktion an einer Nullstelle.
Überlege dann den Verlauf zur zweiten Nullstelle und wie er dort weiterläuft.
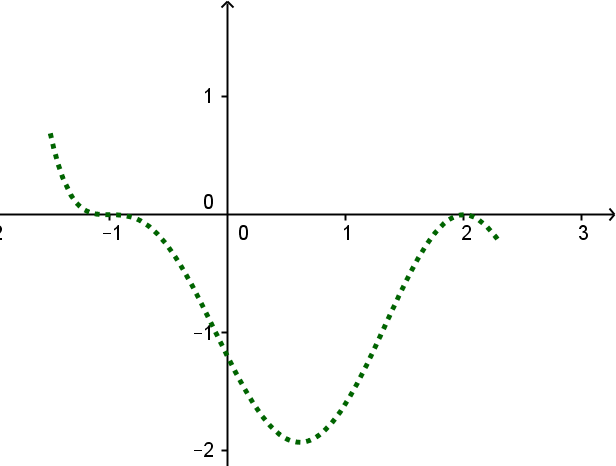
Ergänze jetzt den Graphen noch so, dass er zu einer Funktion vom Grad passt. Dabei ist wichtig, dass der Graph entweder auf beiden Seiten nach oder auf beiden Seiten nach läuft.
Achte darauf, dass die Vielfachheiten der Nullstellen insgesamt höchstens ergeben. Hier ist es eine -fache, eine doppelte und noch eine einfache Nullstelle.
Eine mögliche Lösung
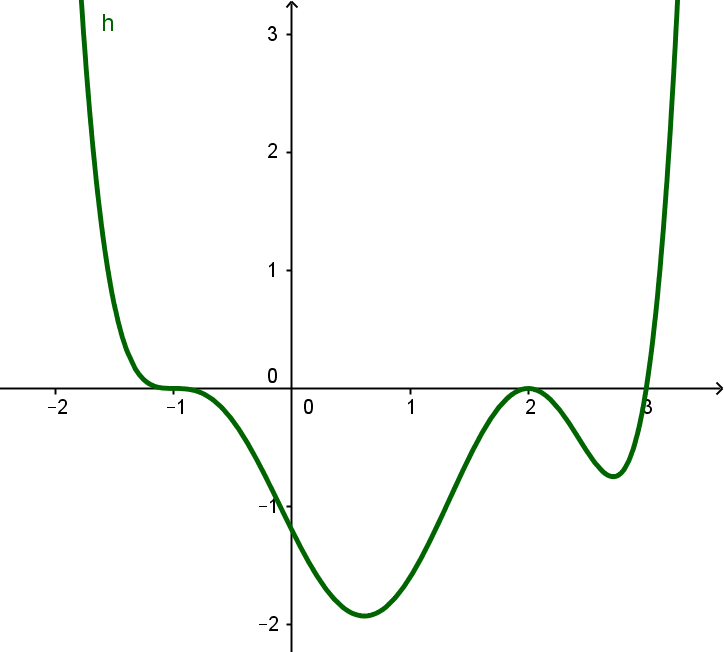
Hast du eine Frage oder Feedback?
- 5
Ordne die Graphen jeweils dem richtigen Funktionsterm zu. Begründe deine Antwort.
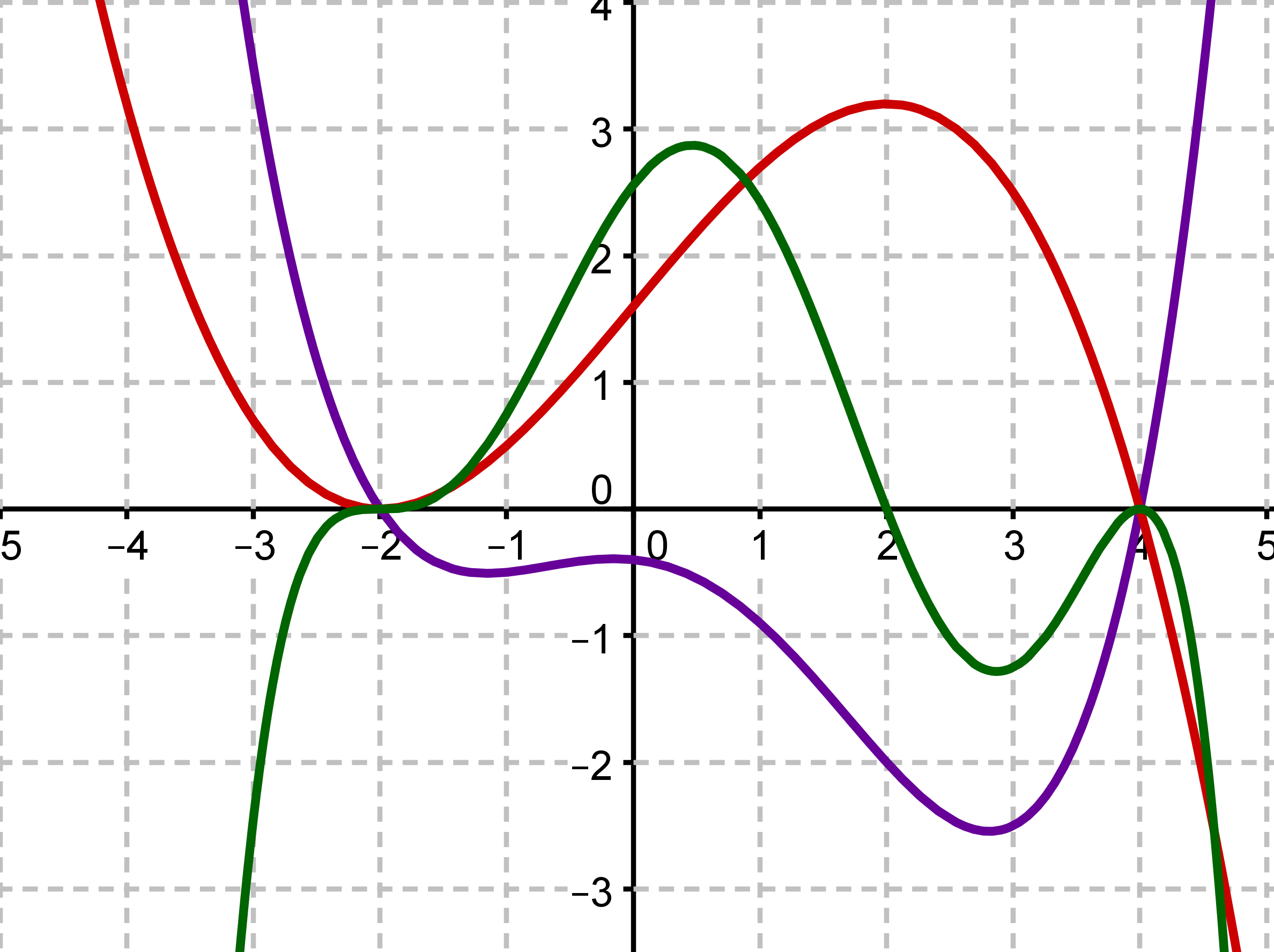
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit von Nullstellen
Roter Graph
Lies als Erstes die Nullstellen der Funktion ab.
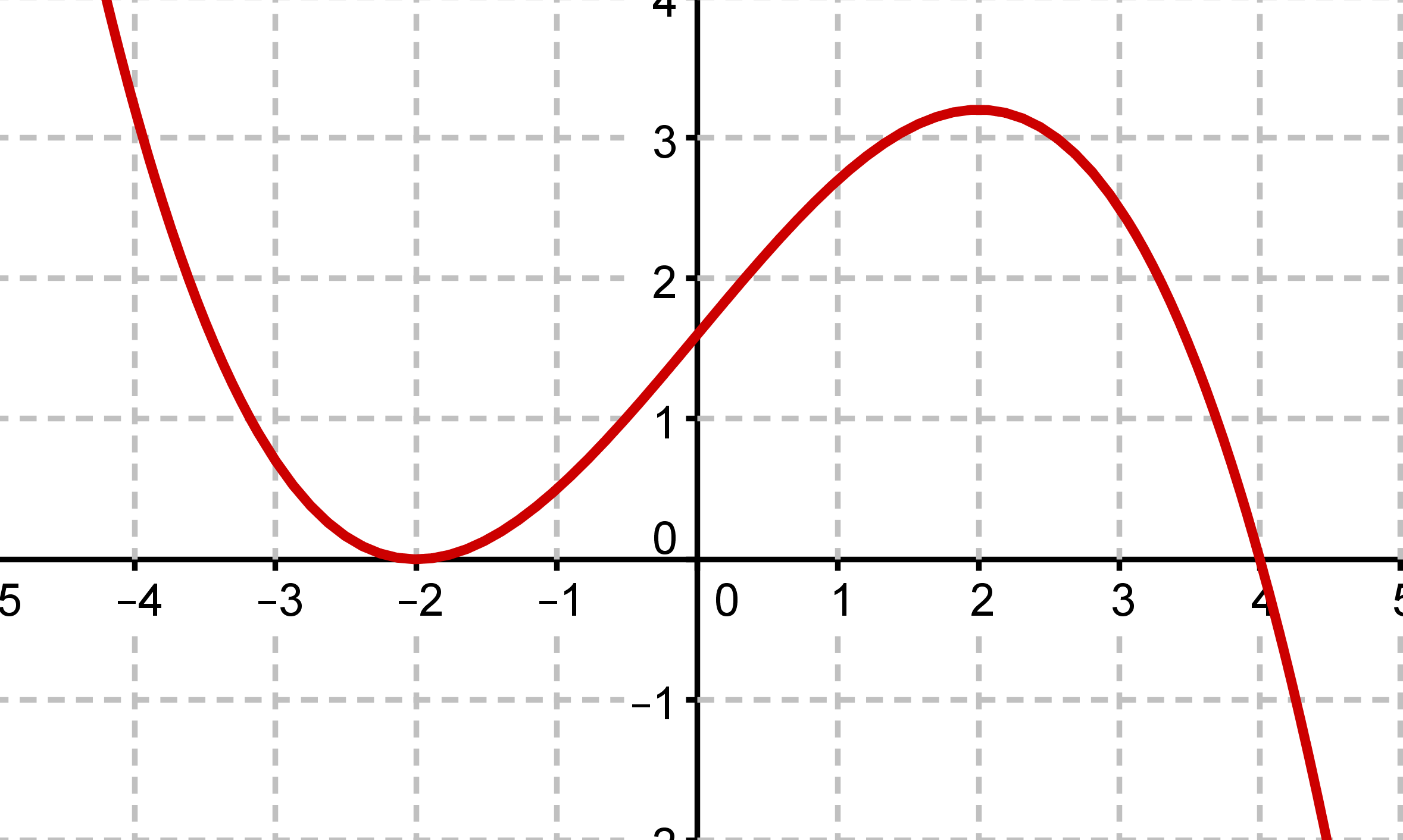
Die Nullstellen des roten Graphen sind bei und .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstelle bei ist eine doppelte Nullstelle, weil sich das Vorzeichen nicht ändert. Die bei ist eine einfache, da sich das Vorzeichen ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da bei eine doppelte und bei eine einfache Nullstelle ist, muss in der Funktion vorkommen. Das ist nur bei der Funktion der Fall.
Lösung: Der rote Graph gehört zu der Funktion .
Grüner Graph
Lies als Erstes die Nullstellen der Funktion ab.
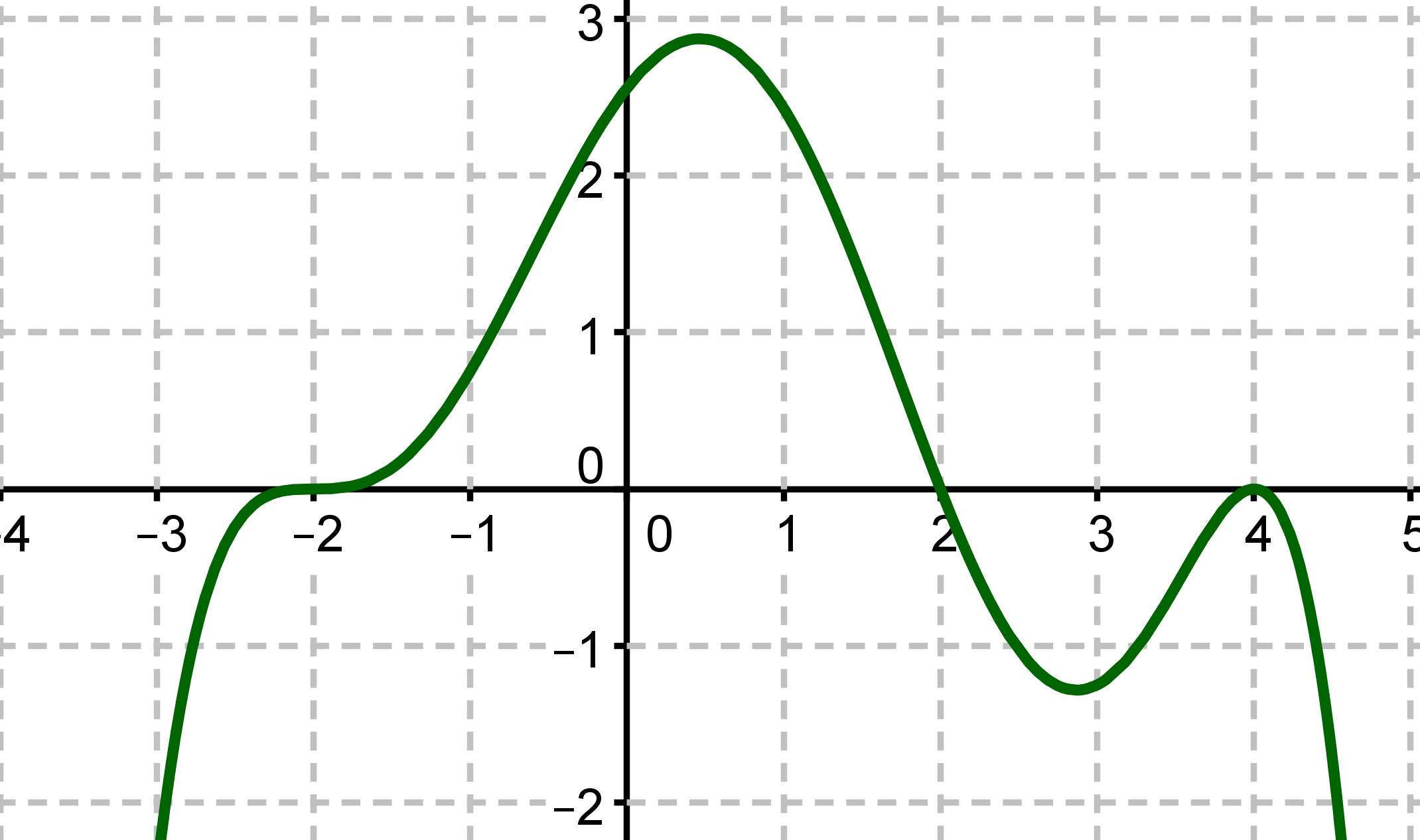
Die Nullstellen des grünen Graphen sind bei , und .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstelle bei ist eine dreifache Nullstelle, weil sich das Vorzeichen ändert und der Graph an der Stelle flach ist. Die bei ist eine einfache, da sich das Vorzeichen ändert. Bei ist es eine doppelte Nullstelle, weil sich das Vorzeichen nicht ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da bei eine dreifache, bei eine einfache und bei eine doppelte Nullstelle ist, muss in der Funktion vorkommen. Das ist nur bei der Funktion der Fall.
Lösung: Der grüne Graph gehört zu der Funktion .
Lila Graph
Lies als Erstes die Nullstellen der Funktion ab.
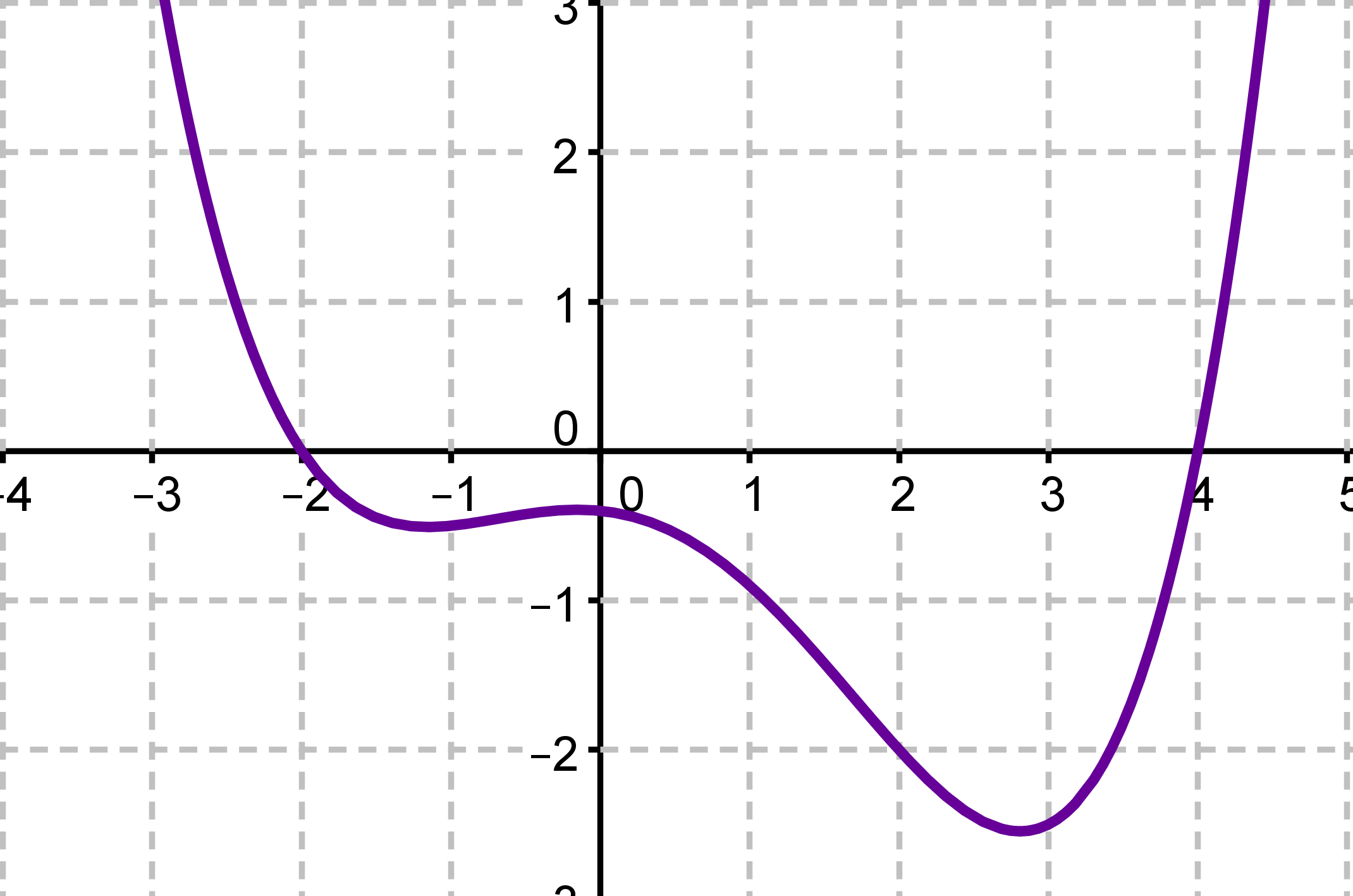
Die Nullstellen des roten Graphen sind bei und .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstellen sind beides einfache Nullstellen, weil sich jedesmal das Vorzeichen ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da sowohl bei als auch bei eine einfache Nullstelle ist, muss in der Funktion vorkommen. Das ist nur bei der Funktion der Fall.
Lösung: Der lila Graph gehört zu der Funktion .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

