Ordne die Graphen jeweils dem richtigen Funktionsterm zu. Begründe deine Antwort.
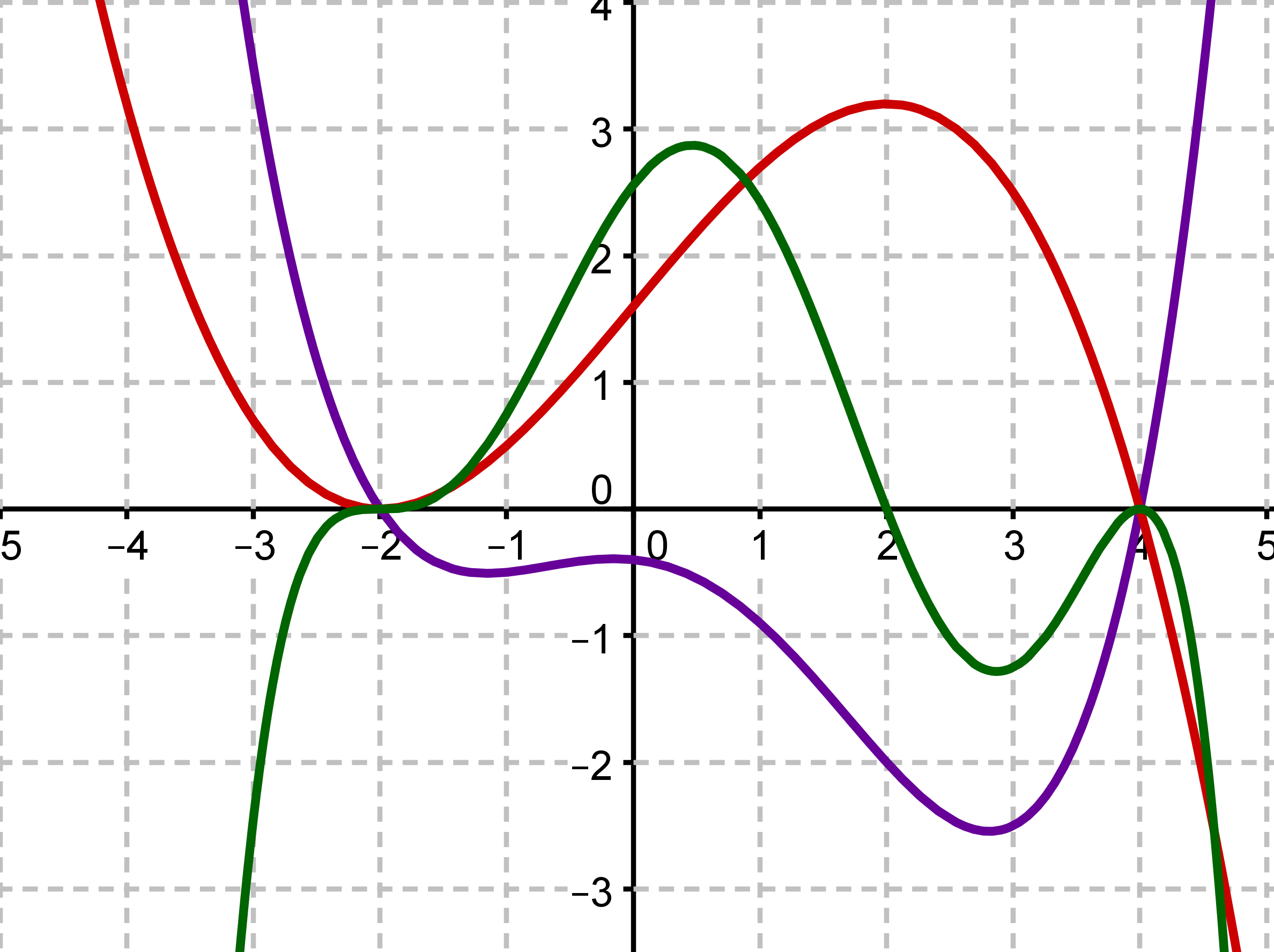
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit von Nullstellen
Roter Graph
Lies als Erstes die Nullstellen der Funktion ab.
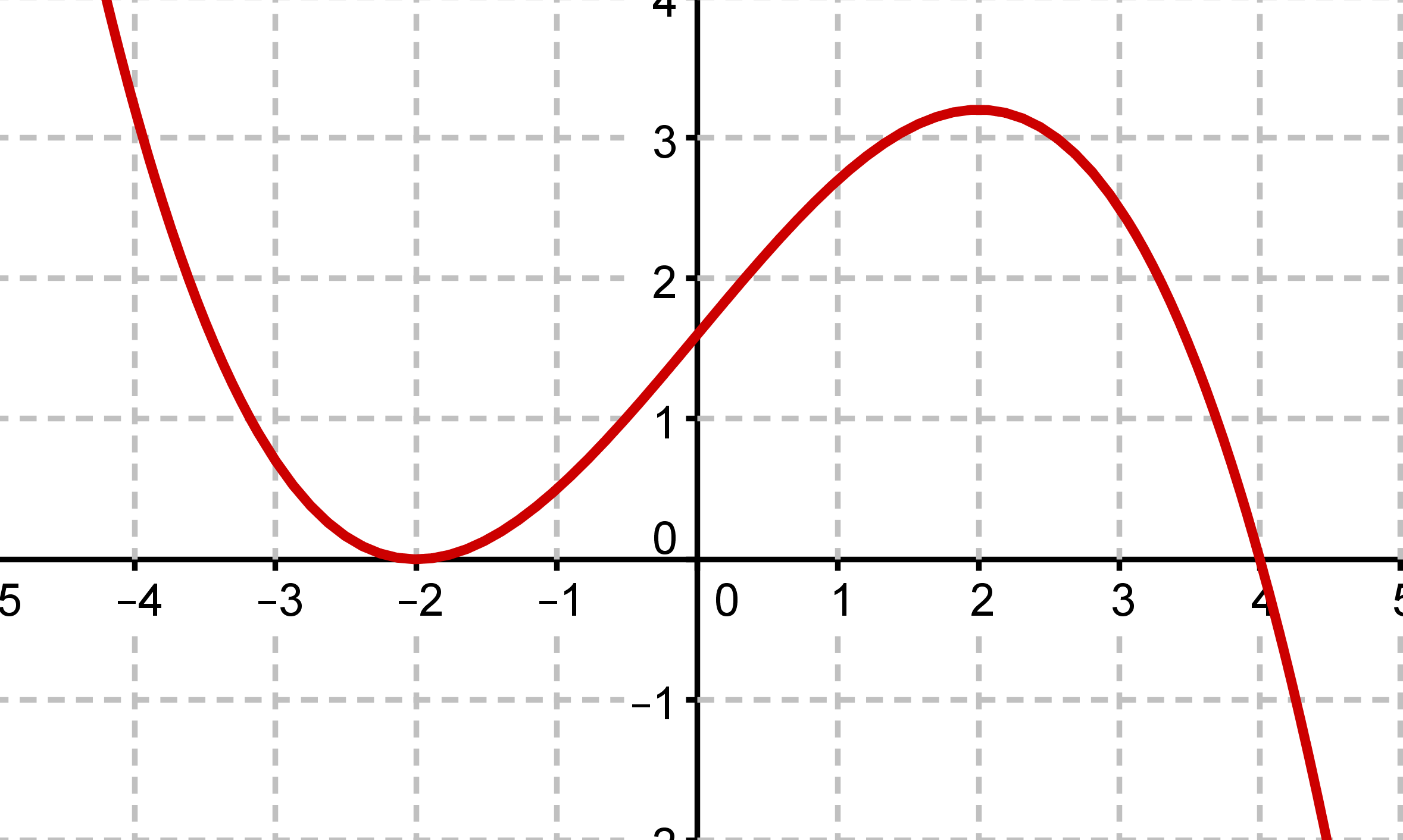
Die Nullstellen des roten Graphen sind bei und .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstelle bei ist eine doppelte Nullstelle, weil sich das Vorzeichen nicht ändert. Die bei ist eine einfache, da sich das Vorzeichen ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da bei eine doppelte und bei eine einfache Nullstelle ist, muss in der Funktion vorkommen. Das ist nur bei der Funktion der Fall.
Lösung: Der rote Graph gehört zu der Funktion .
Grüner Graph
Lies als Erstes die Nullstellen der Funktion ab.
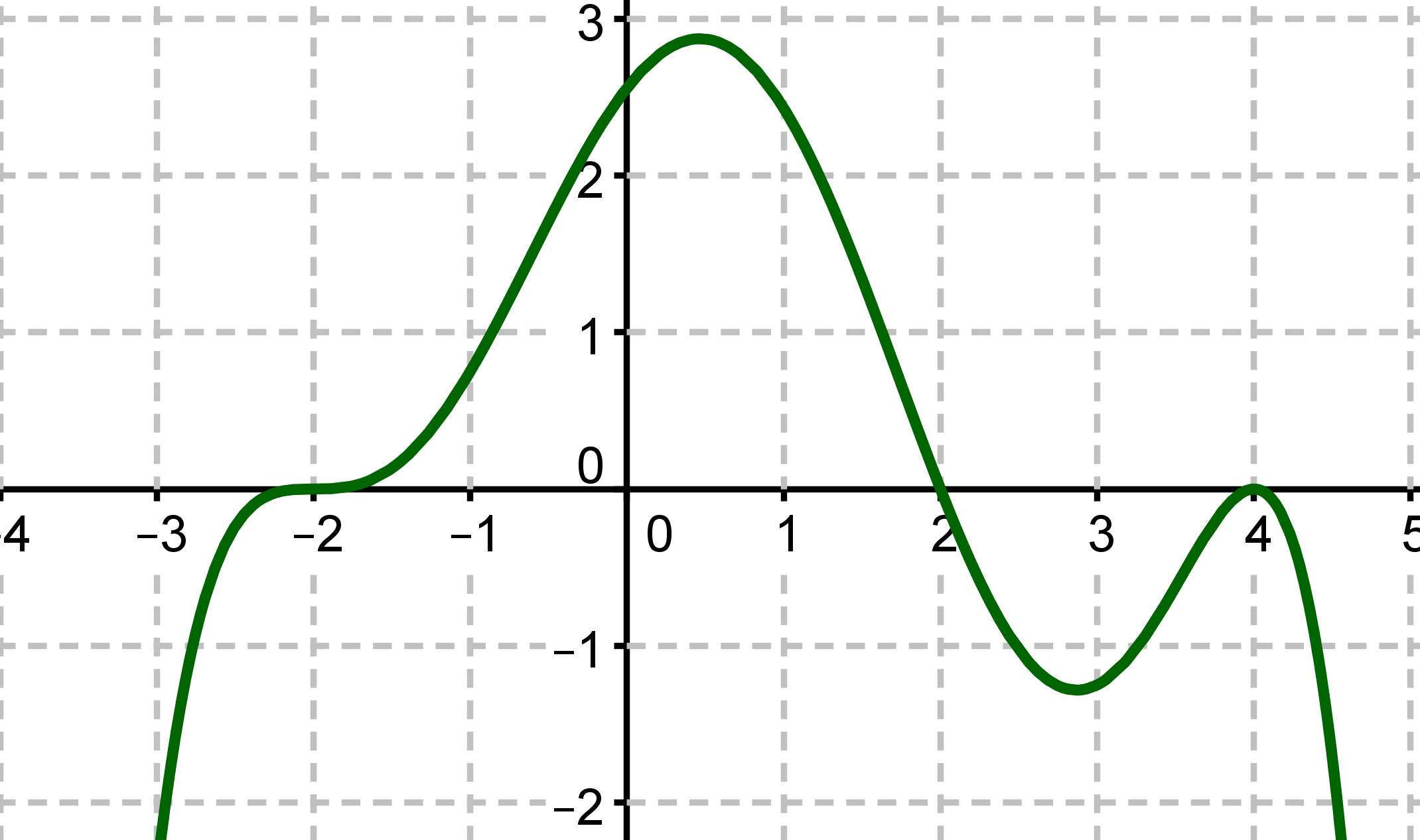
Die Nullstellen des grünen Graphen sind bei , und .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstelle bei ist eine dreifache Nullstelle, weil sich das Vorzeichen ändert und der Graph an der Stelle flach ist. Die bei ist eine einfache, da sich das Vorzeichen ändert. Bei ist es eine doppelte Nullstelle, weil sich das Vorzeichen nicht ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da bei eine dreifache, bei eine einfache und bei eine doppelte Nullstelle ist, muss in der Funktion vorkommen. Das ist nur bei der Funktion der Fall.
Lösung: Der grüne Graph gehört zu der Funktion .
Lila Graph
Lies als Erstes die Nullstellen der Funktion ab.
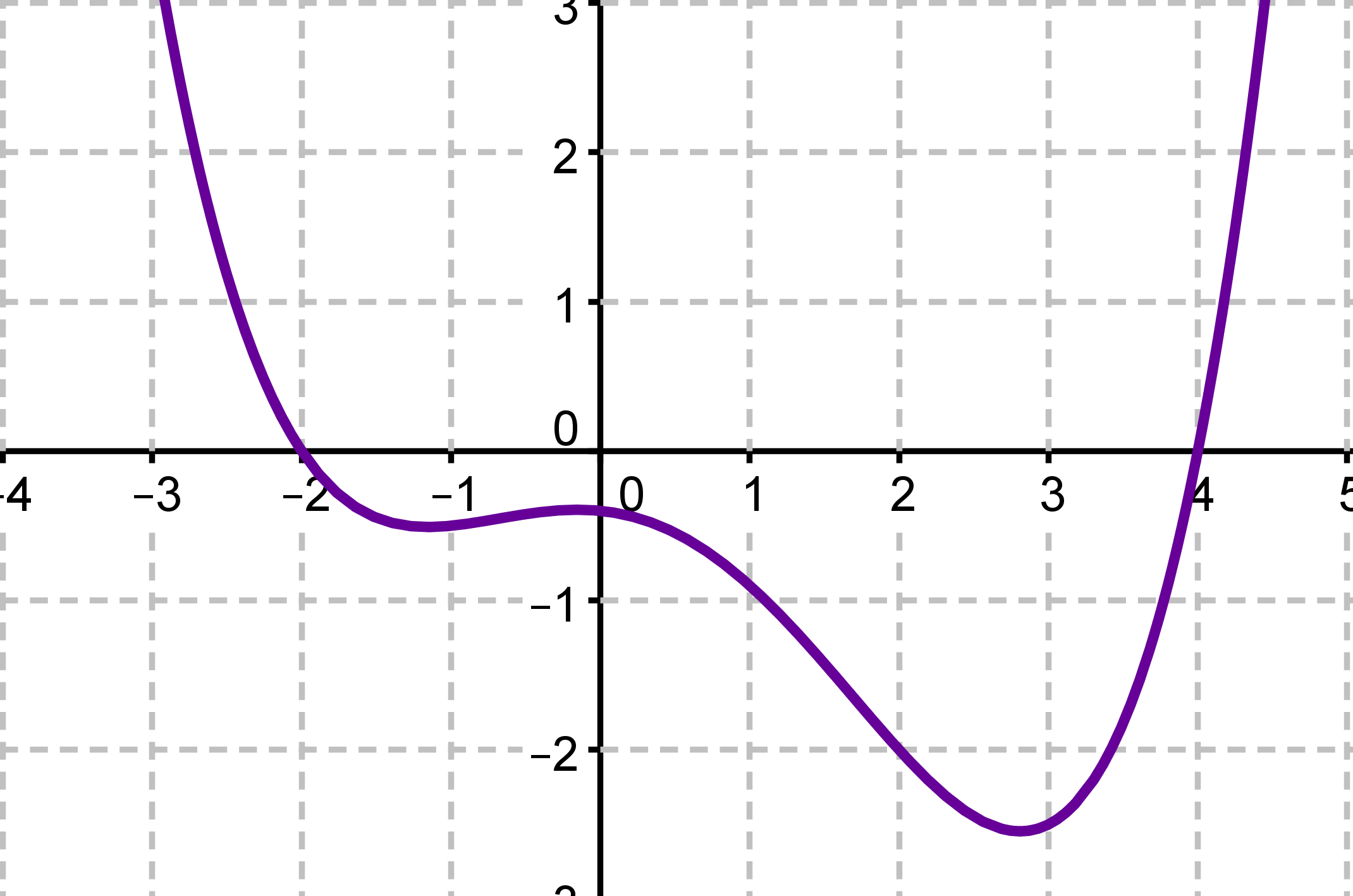
Die Nullstellen des roten Graphen sind bei und .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstellen sind beides einfache Nullstellen, weil sich jedesmal das Vorzeichen ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da sowohl bei als auch bei eine einfache Nullstelle ist, muss in der Funktion vorkommen. Das ist nur bei der Funktion der Fall.
Lösung: Der lila Graph gehört zu der Funktion .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
