1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du die ganzen Zahlen als Erweiterung der natürlichen Zahlen kennen.
Vorkenntnisse
Du solltest bereits die natürlichen Zahlen und die Grundrechenarten kennen.
Kursdauer
Der Kurs dauert ungefähr 1 Stunde.
2 Negative Zahlen im Alltag
Neben den natürlichen Zahlen triffst du im Alltag auch auf folgende Darstellungen:
Dieses Bild kommt aus einem Aufzug.
Du weißt vielleicht schon, dass...
... die 0 für Erdgeschoss steht.
... die Stockwerke -2 und -1 unter dem Erdgeschoss liegen.
... der erste Stock oberhalb vom Erdgeschoss liegt.

Auch im Bereich des Geldwesens ist es möglich, auf Zahlen zu stoßen, die nicht in den natürlichen Zahlen enthalten sind.
Hier sieht man beispielsweise einen Kontoauszug. Auf diesem steht vor dem neuen Kontostand ein Minus. Man spricht in diesem Fall von Schulden.

Wie du siehst, gibt es Zahlen, wie zum Beispiel "" beim Aufzug, die wir noch nicht aus den natürlichen Zahlen kennen.
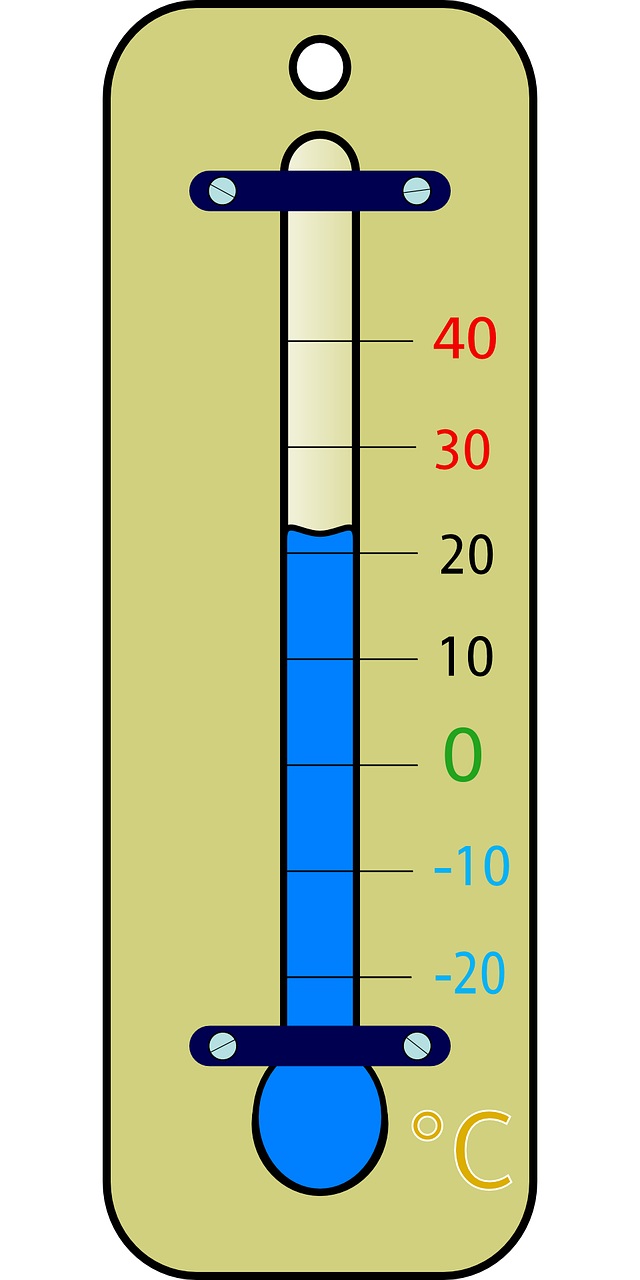
Eventuell sind dir auch schon mal Thermometer (also Temperaturmessgeräte) aufgefallen, die eine negative Zahl anzeigen. Das tritt häufig im Winter auf, wenn es sehr kalt ist. Man spricht dann davon, dass die Temperatur unter den Gefrierpunkt (also unter ) gesunken ist. Dies kennzeichnet man durch das Minus.
3 Die ganzen Zahlen und der Zahlenstrahl
Negative Zahlen auf dem Zahlenstrahl
Wie können diese negativen Zahlen im bisher bekannten Zahlenstrahl dargestellt werden?
Hierfür muss der Zahlenstrahl erweitert werden. Wie bei einem flach liegenden Thermometer, werden links von der Null nun die negativen Zahlen ergänzt.
Zahlengerade
Der Zahlenstrahl muss für die negativen Zahlen ins Negative verlängert werden.
Diesen verlängerten Zahlenstrahl nennt man Zahlengerade.

Zahlengerade mit den negativen Zahlen in Lila, der 0 in Orange und den natürlichen Zahlen in Grün.
Beachte: Nur am rechten Ende der Zahlengeraden befindet sich ein Pfeil.
Der Pfeil zeigt immer in die Richtung der größeren Zahlen und die negativen Zahlen sind, wie auch die negativen Temperaturen, kleiner als die positiven.
Die ganzen Zahlen
Der bekannte Zahlenraum der natürlichen Zahlen wurde nun um die negativen Zahlen erweitert:
Ganze Zahlen bestehen aus den negativen Zahlen, der Null und den positiven Zahlen.
Das Symbol für die ganzen Zahlen ist .
4 Beispiele zum Größenvergleich ganzer Zahlen
Weiterhin gilt für den Größenvergleich von Zahlen die einfache Regel:
Was auf der Zahlengeraden weiter rechts liegt, ist größer.
Beispielaufgabe: Welche Zahl ist größer?
oder ?
Lösung:
-10 ist als negative Zahl in jedem Fall kleiner als die positive Zahl 5
5 liegt auf der Zahlengeraden weiter rechts und ist somit größer.
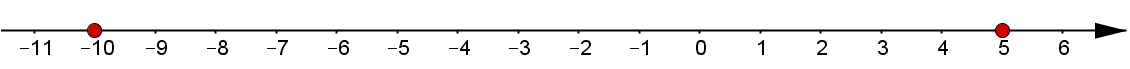
oder ?
Lösung:
Auch hier gilt: Eine negative Zahl liegt immer weiter links auf der Zahlengeraden als eine positive Zahl oder als die Null. Somit ist 0 die größere Zahl.
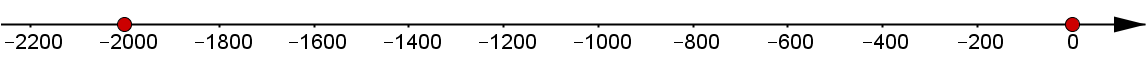
oder ?
Lösung:
-7 liegt auf der Zahlengeraden weiter links als -5 und ist somit die kleinere Zahl.
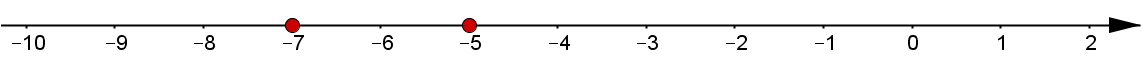
Obwohl natürlich 7 größer als 5 ist, ist -7 kleiner als -5.
5 Aufgaben zum Größenvergleich
Richtig oder falsch?
Laden
Laden
Laden
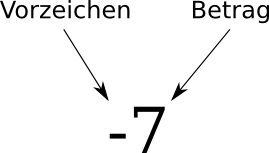
6 Vorzeichen und Betrag
Eine negative Zahl ist also aus zwei Komponenten aufgebaut:
Das Minus ist hier ein Vorzeichen.
Die Ziffern dahinter nennt man den Betrag einer Zahl.
Manchmal tritt auch ein Plus als Vorzeichen auf, um eine Zahl ausdrücklich als positiv zu kennzeichnen, z. B. bei +5.
und können also auch Vorzeichen sein.
Schreibweise für den Betrag
Möchtest du explizit den Betrag einer Zahl beschreiben, gibt es dafür folgende Schreibweise:
Beispiele:
7 Vergleich der ganzen Zahlen mit den natürlichen Zahlen - Fragestellung
Nun hast du die ganzen Zahlen bereits kennengelernt.
Doch wie hängt diese Zahlmenge mit den natürlichen Zahlen zusammen und was ändert sich bei Betrachtung der Menge der ganzen Zahlen im Vergleich zu den natürlichen Zahlen?
Versuche hier zunächst selbst Gemeinsamkeiten und Unterschiede zu finden.
8 Vergleich der ganzen Zahlen mit den natürlichen Zahlen - Auflösung
Vielleicht hast du ja bereits ein paar der folgenden Unterschiede und Gemeinsamkeiten gefunden.
Gemeinsamkeiten
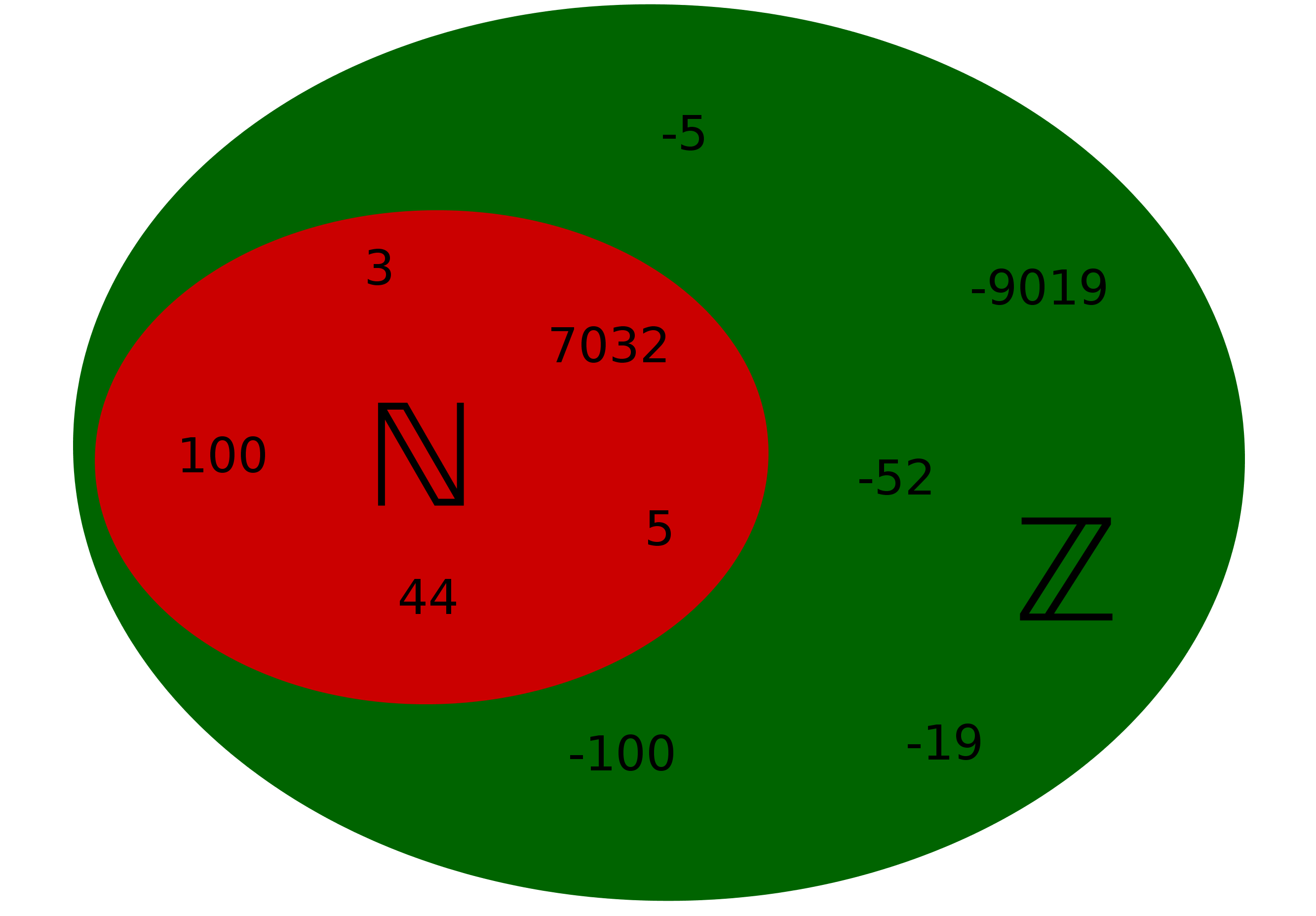
Wie du vielleicht beim Umkippen des Thermometers oder in der Definition der ganzen Zahlen festgestellt hast, sind die natürlichen Zahlen in den ganzen Zahlen enthalten.
Hierbei ist es auch egal, ob die natürlichen Zahlen oder die natürlichen Zahlen mit der Null gemeint sind, denn beide sind in den ganzen Zahlen enthalten.
Unterschiede
Natürliche Zahlen | Ganze Zahlen |
|---|---|
Es gibt eine kleinste Zahl, nämlich die Eins. In gibt es keine Zahl, die kleiner als die Eins ist. | Es gibt KEINE kleinste Zahl mehr. Die ganzen Zahlen haben keine kleinste Zahl. Du kannst von jeder ganzen Zahl auf dem Zahlenstrahl nach links gehen und du landest bei einer kleineren Zahl. |
Die Größe einer Zahl kann direkt an den Ziffern abgelesen werden. Jede Zahl ist positiv. | Jede Zahl hat ein Vorzeichen (). Das beeinflusst die Größe einer Zahl und deren Lage auf der Zahlengeraden. |
9 Zusammenfassung
In diesem Kurs konntest du sehen, dass im Alltag auch negative Zahlen auftreten, z.B. beim Thermometer.
Deshalb wurde eine neue Zahlmenge eingeführt, die nun auch die negativen Zahlen enthält; das ist die…
Menge der ganzen Zahlen
Diese ist folgendermaßen definiert:
wobei die negativen Zahlen ein negatives Vorzeichen (ein Minus) haben.
Beachte: Das in der Formel verwendete ist mathematisch nicht richtig, aber verständlicher.
Also
Außerdem hast du gesehen, dass in enthalten ist.
Allerdings gilt in nicht mehr alles, was in noch galt. Hierzu zählt zum Beispiel, dass es in kein kleinstes Element mehr gibt.
10 Zeig was du kannst!
Größenvergleich
Ordne folgende Zahlen der Größe nach. Beginne mit der kleinsten.
Laden
Betrag
Berechne folgende Ausdrücke:
a)
Laden
b)
Laden
