Aufgaben zur Polynomdivision - lernen mit Serlo!

Tintenkleckse

Was verbirgt sich dahinter?

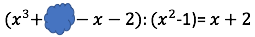
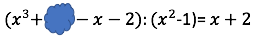
Setze a für den gesuchten Klecks und starte mit der Multiplikationsprobe der Division
$Wert des Quotienten \cdot Divisor = Dividend$
$\begin{array}{lcl} (x + 2) \cdot (x^{2} - 1) & = & x^{3} + a - x - 2 \\ x^{3} - x + 2 x^{2} - 2 & = & x^{3} + a - x - 2 \\ a & = & 2 x^{2} \end{array}$
Löse die Gleichung nach $a$ auf.
Der Tintenklecks verdeckt den Term $2 x^{2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
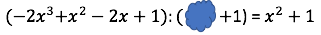
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
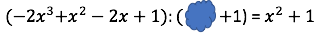
Setze $a$ für den gesuchten Klecks und starte mit der Multiplikationsprobe der Division:
$Wert des Quotienten \cdot Divisor = Dividend$
$\begin{array}{lcl} (x^{2} + 1) \cdot (a + 1) & = & - 2 x^{3} + x^{2} - 2 x + 1 \\ a x^{2} + x^{2} + a + 1 & = & - 2 x^{3} + x^{2} - 2 x + 1 \\ a (x^{2} + 1) & = & - 2 x^{3} - 2 x \\ a (x^{2} + 1) & = & - 2 x (x^{2} + 1) \\ a & = & - 2 x \end{array}$
Löse die Gleichung nach a auf.
Der Tintenklecks verdeckt den Term $- 2 x$ .
Alternative Lösung über die Polynomdivision
$(- 2 x^{3} + x^{2} - 2 x + 1) : (a + 1) = x^{2} + 1$
Starte die Polynomdivision
Schon der erste Schriit des Verfahrens der Polynomdivision ergibt einen Wert für $a$ :
$\begin{array}{lcl} - 2 x^{3} : a & = & x^{2} | \cdot a \\ - 2 x^{3} & = & a \cdot x^{2} | : x^{2} \\ \Rightarrow a & = & - 2 x \end{array}$
Es ist allerdings noch nachzurechnen, dass die Polynomdivision mit diesem Wert für $a$ auch wirklich aufgeht.
$\begin{array}{l} (- 2 x^{3} + x^{2} - 2 x + 1) : (- 2 x + 1) = x^{2} + 1 \\ - (- 2 x^{3} + x^{2}) \\ - 2 x + 1 \\ - (- 2 x + 1) \\ 0 \end{array}$
Die Polynomdivision geht also mit $a = - 2 x$ tatsächlich auf. Der Tintenklecks ist entzaubert!
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
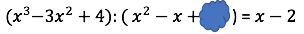
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
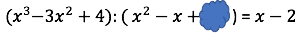
Setze $a$ für den gesuchten Klecks ein und starte mit der Multiplikationsprobe der Division.
$Wert des Quotienten \cdot Divisor = Dividend$
$\begin{array}{lcl} (x - 2) \cdot (x^{2} - x + a) & = & x^{3} - 3 x^{2} + 4 \\ x^{3} - x^{2} + a x - 2 x^{2} + 2 x - 2 a & = & x^{3} - 3 x^{2} + 4 \\ x^{3} - 3 x^{2} + 2 x + a (x - 2) & = & x^{3} - 3 x^{2} + 4 \\ a (x - 2) & = & 4 - 2 x \\ a (x - 2) & = & - 2 (x - 2) | : (x - 2) \\ a & = & - 2 \end{array}$
Löse die Gleichung nach $a$ auf.
Der Tintenklecks verdeckt die Zahl $- 2$ .
Alternative Lösung über die Polynomdivision
$\begin{array}{l} (x^{3} - 3 x^{2} + 4) \cdot (x^{2} - x + a) = x - 2 \\ - (x^{3} - x^{2} + a x) \\ - 2 x^{2} - a x + 4 \\ - (- 2 x^{2} + 2 x - 2 a) \\ - (\underset{0!}{\underset{⏟}{a + 2}}) x + (\underset{0!}{\underset{⏟}{4 + 2 a}}) \end{array}$
Die Polynomdivision geht genau für $a = - 2$ auf.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?