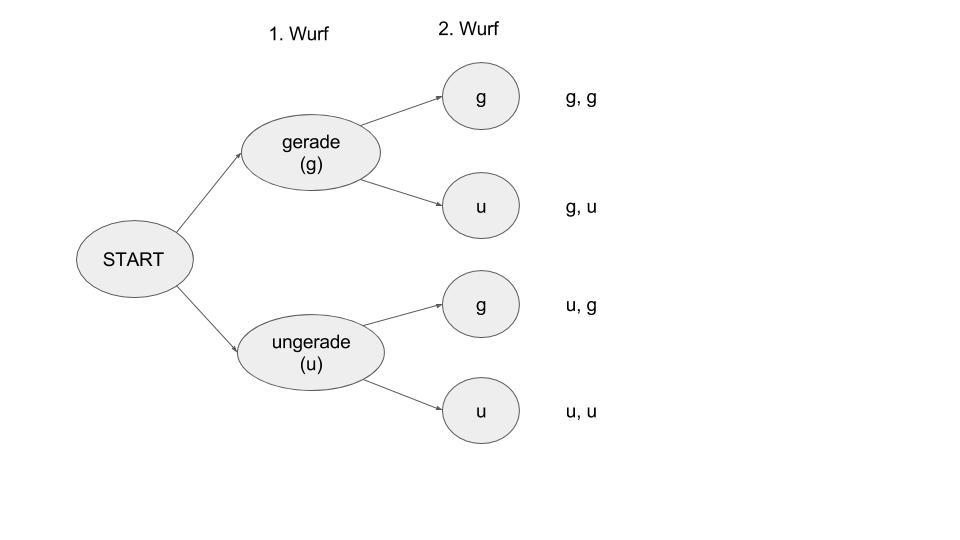
Zwei Personen einigen sich auf ein Würfelspiel bei dem ein sechs-seitiger Würfel zweimal geworfen wird und die Summe aus beiden Würfen als Ergebnis notiert wird. Wie mächtig ist der Ergebnisraum?
Wie mächtig ist der Ergebnisraum?
Handelt es sich bei dem Spiel um ein Laplace-Experiment?
Bei welchem der folgenden Experimente handelt es sich um ein Laplace-Experiment?
Der erste Spieler würfelt eine 10. Wie hoch ist die Wahrscheinlichkeit, dass der zweite Spieler eine höhere Summe würfelt und das Spiel gewinnt, in ganzen Prozent? (Runde dein Ergebnis auf die nächste ganze Zahl, um es zu überprüfen: 0,3675 → 37 (%).)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?