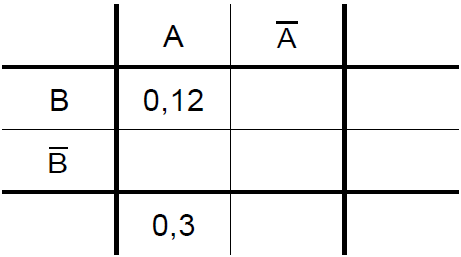
Nebenstehende Vierfeldertafel gehört zu einem Zufallsexperiment mit den stochastisch unabhängigen Ereignissen A und B. Tragen Sie alle fehlenden Wahrscheinlichkeiten ein.
Im Vorfeld einer Wahl wird eine wahlberechtigte Person zufällig ausgewählt und befragt. Betrachtet werden folgende Ereignisse:
C: "Die Person ist älter als 50 Jahre."
D: "Die Person will die derzeitige Regierungspartei wählen."
Erläutern Sie, was in diesem Sachzusammenhang eine stochastische Unabhängigkeit der Ereignisse C und D bedeuten würde.
