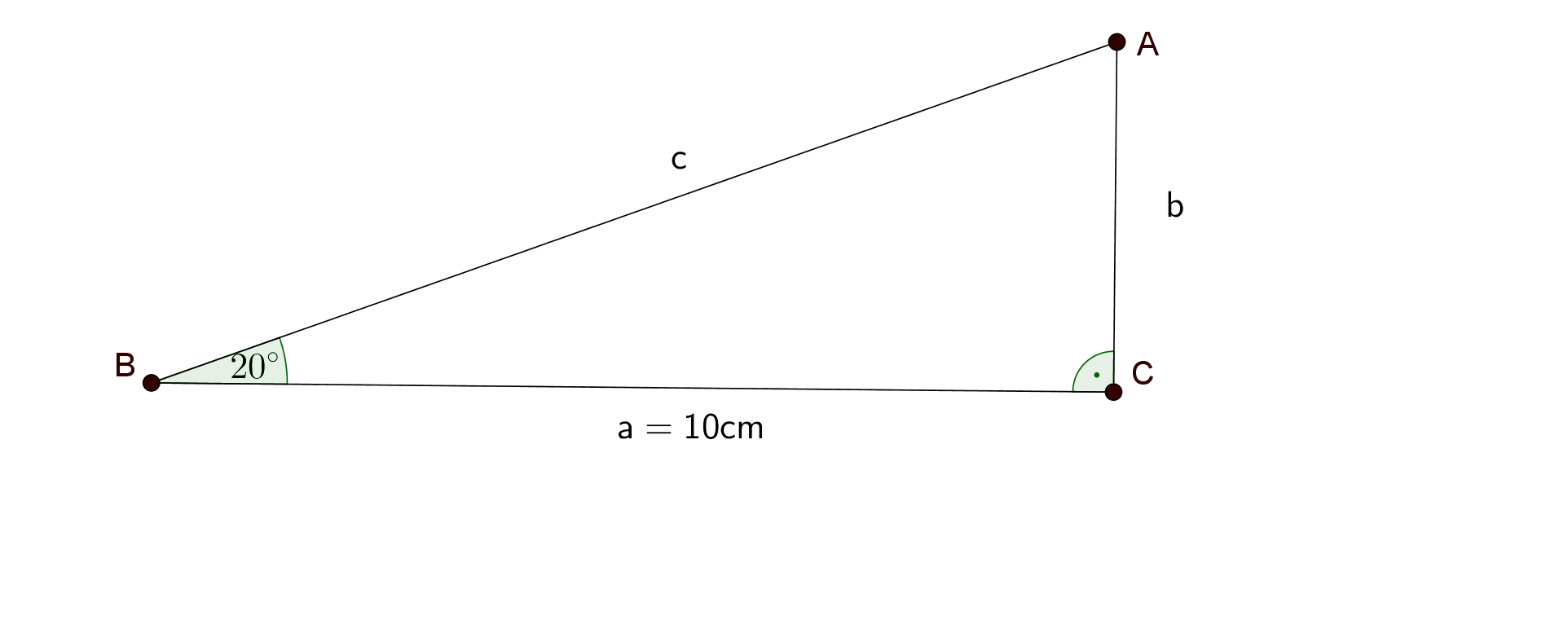
Bestimmen Sie für mithilfe einer beschrifteten Zeichnung sowie geeigneter Messungen einen möglichst genauen Näherungswert. Geben Sie Ihren Näherungswert in dezimaler Schreibweise mit zwei Nachkommastellen an. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?