1 Das Ziegenproblem
Herzlich willkommen in der Serlo-Gameshow

Du bist Kandidat bei einer Gameshow die schon jahrelang läuft.
In der Show haben die Kandidaten die Möglichkeit, entweder ein tolles Auto oder eine Ziege, also eine Niete, zu gewinnen. Der Kandidat wählt eines der drei gleich aussehenden Tore aus.
Der Moderator Monty öffnet immer nach der Wahl des Kandidaten eines der beiden anderen Tore noch geschlossenen Tore. Er öffnet immer das mit einer Ziege und bietet dem Kandidaten an, das Tor noch einmal zu wechseln.
Stell dir vor, du hast ein Tor - zum Beispiel Tor 1 - gewählt und der Moderator Monty hat ein weiteres Tor geöffnet, hinter dem eine Ziege steht. Der Moderator Monty sagt: "Bleiben Sie bei der gewählten Tür, oder wollen Sie noch einmal wechseln?"
Jetzt, wo du noch vor zwei geschlossenen Toren stehst, hast du die Wahl: Bleibst du bei deinem ausgewählten Tor oder wechselst du noch einmal?
Denkst du, das macht einen Unterschied? Das erfährst du in diesem Kurs!
2 Neues Spiel, neue Tore!
Jetzt bist du dran! Lass uns spielen!
Du siehst drei Türen. Wähle eine Tür aus, indem du auf die entsprechende Beschriftung klickst.
Dann öffnet der Moderator eine Tür, hinter der eine Ziege steht und fragt, ob du wechseln möchtest.
Du kannst das Spiel auch mehrfach spielen und dir schon eine Meinung erzeugen, ob "wechseln" oder "bleiben" besser ist.
Hast du dir ein- oder mehrere Male ein Auto verdient:
Herzlichen Glückwunsch! Du hast gewonnen.
Sonst: Schade, aber Ziegen sind tolle Tiere!
Bei einem einzelnen oder wenigen Spielen, ist es immer schwer zu beurteilen, ob es klug ist, das Tor im zweiten Schritt zu wechseln oder nicht.
Doch die Mathematik kann uns helfen herauszufinden, was statistisch - also bei häufigem Spielen des Spiels - das Klügere ist.
Es gibt drei wesentliche "Denkweisen":
Wechseln ist das Beste!
Nicht wechseln ist das Beste!
Es ist egal, ob man wechselt!
Welche denkst du, ist die richtige?
Auf den nächsten Seiten bekommst du 6 Denkansätze vorgestellt. Richtige und Falsche.
3 1. Denkweise von Mick
Ich habe am Anfang Tor 1 gewählt.

Fall A: Der Moderator öffnet Tür 3. Dann ist das Ereignis "Preis nicht hinter 3" , also "Preis hinter 1 oder Preis hinter 2" eingetroffen. Daher können wir mit bedingten Wahrscheinlichkeiten weiterarbeiten. Die bedingte Wahrscheinlichkeit "Preis hinter 1, falls nicht hinter 3" ist und die Wahrscheinlichkeit "Preis hinter 2, falls nicht hinter 3" ist .
Fall B: Der Moderator öffnet Tür 2. Die Denkweise ist wie beim Fall A.
Mick ist nach dieser Überlegung der Meinung, es ist egal ob man wechselt.
Mick liegt damit falsch.

Begründung:
Die Argumentation ist zwar nicht falsch, gehört aber nicht zu dem vorgegebenen Experiment, sondern zu folgendem:
Der Showmaster öffnet zuerst eine Tür, hinter der eine Niete ist.
Der Kandidat soll sich dann zwischen einer der anderen Türen entscheiden.
Das ist nicht dasselbe Experiment!
4 2. Denkweise von Mila
Ich habe am Anfang Tor 1 gewählt.

Nun gibt es vier Fälle:
Fall | Auto hinter Nr.: | Moderator öffnet Nr.: | richtige Strategie |
|---|---|---|---|
I | 1 | 2 | nicht Wechseln |
II | 1 | 3 | nicht Wechseln |
III | 2 | 3 | Wechseln |
IV | 3 | 2 | Wechseln |
Zwei von vier Fällen ergeben die richtige Strategie, also Gewinn. Also ist die Wahrscheinlichkeit jeweils !
Mila ist nach dieser Überlegung der Meinung, es ist egal ob man wechselt.
Mila liegt damit falsch.

Begründung:
Die Überlegung wäre korrekt, wenn die Fälle I bis IV gleichwahrscheinlich wären. Die Fälle I bis IV sind aber nicht gleichwahrscheinlich. Dies kann man an einem Baumdiagramm leicht nachvollziehen:

Im Baumdiagramm ist die erste Stufe das "Verstecken des Autos", die zweite Stufe ist das "Öffnen" durch den Moderator.
Mit den Pfadregeln kann man leicht ausrechnen, dass
(da der Moderator ja dann Tor 3 öffnen muss)
(da der Moderator ja dann Tor 2 öffnen muss)
5 3. Denkweise von Helen
Ich habe am Anfang Tor 1 gewählt.

Der Moderator weiß, dass ich das richtige Tor gewählt habe und will mich deshalb abbringen. Also sollte ich bei meiner Wahl bleiben.
Damit liegt Helen falsch.

Begründung:
Lese die Aufgabe genau. Da steht: „Du bist Kandidat bei einer Gameshow, die schon jahrelang läuft. "
Der Moderator öffnet also seit Jahren eine der nicht gewählten Türen. Unabhängig, ob der Kandidat richtig geraten hat oder nicht.
6 4. Denkweise von Jim
Ich habe am Anfang Tor 1 gewählt.

Das Auto wird vor Beginn der Show platziert. Wenn ich bei der ersten Wahl richtig gelegen habe, dann spielt das Öffnen der Tür keine Rolle.
Ich bleibe bei Tür 1.
Damit liegt Jim falsch.

Begründung:
Erklären kann man die falsche Denkweise am besten durch ein anderes Experiment - das einmalige Würfeln.
Du kannst wählen, ob du bei gleichem Gewinn auf die 6 setzt, oder auf die ungeraden Zahlen.
Auch hier kann natürlich genauso die 6 fallen. Aber du wirst wahrscheinlich auf die ungeraden Zahlen setzen, da hier die Wahrscheinlichkeit zu gewinnen höher ist.
Bei den Toren versperrt nur das „Drumherum“ den Blick. Eigentlich ist es doch die Wahl, ob Du ein Tor wählst (nämlich das, was du zu Beginn gewählt hast) oder ob du zwei Tore gleichzeitig wählst (nämlich das vom Moderator geöffnete und das andere geschlossene).
7 5. Denkweise von Sirena
Ich habe am Anfang Tor 1 gewählt.

Die Wahrscheinlichkeit, dass ich gleich das richtige Tor gewählt habe, ist .
Dann ist die Wahrscheinlichkeit, dass sich das Auto nicht hinter dem gewählten Tor befindet .
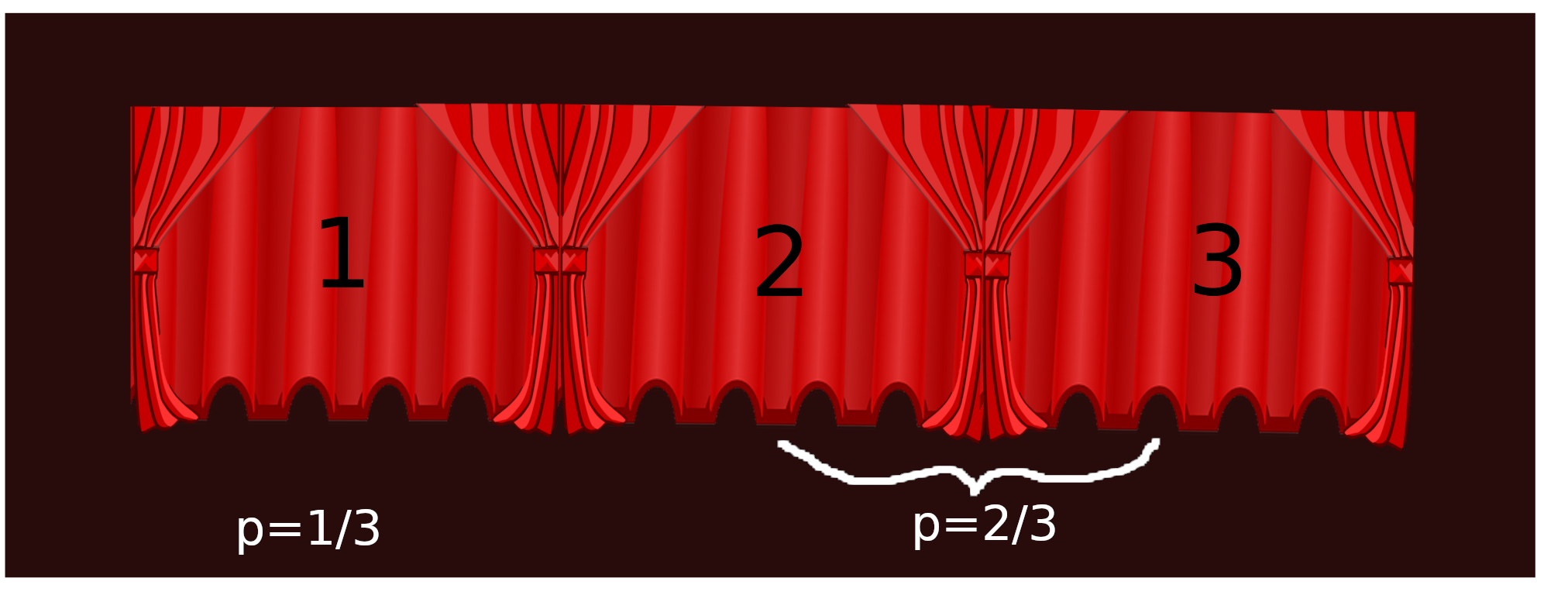
Der Moderator gibt mir eine zusätzliche Information über den Standort des Autos! Er öffnet zum Beispiel Tor drei. Hinter diesem muss eine Ziege sein.
Ich erfahre also, wie sich die Wahrscheinlichkeit auf die nicht gewählten Tore verteilen.
Die Wahrscheinlichkeit für mein gewähltes Tor verändert sich nicht. Also muss das Tor 2 die Wahrscheinlichkeit erhalten.
Wenn ich nun wechsle, habe ich mit Wahrscheinlichkeit das richtige Tor, also das
Auto gewonnen.
Sirena liegt damit richtig.

8 6. Denkweise von Norbert
Ich habe am Anfang Tor 1 gewählt.

Es gibt ja nur drei Türen, und hinter einer muss das Auto stehen. Die drei – gleich wahrscheinlichen – Möglichkeiten lauten:
Erstens: Das Auto steht hinter Tür eins. Dann sollte ich bei der Tür bleiben.
Zweitens: Das Auto steht hinter Tür drei. Dann muss der Showmaster natürlich Tür zwei öffnen. Denn er darf nicht das Auto hinter Tür drei zeigen, und er darf auch nicht enthüllen, ob ich mit Tür eins richtig liege. In diesem Fall ist also das Wechseln zur verbleibenden Tür drei vorteilhaft.
Drittens: Das Auto steht hinter Tür zwei. Dies ist wie der letzte Fall, der Showmaster muss diesmal Tür drei öffnet. Wieder verhilft Wechseln zur verbleibenden Tür zum Gewinn.
Fazit: Wer wechselt, gewinnt in zwei von drei Fällen.
Norbert liegt damit richtig.

9 Erklärung der korrekten Stategie
Am sogenannten Ziegenproblem bissen sich sogar Nobelpreisträger die Zähne aus.
Kaum eine andere mathematische Denkaufgabe hat die Gemüter von Mathematikern so erhitzt wie das sogenannte Ziegenproblem. Denn dem normalen, angeblich "gesunden", Menschenverstand läuft die mathematisch korrekte Lösung zuwider.
Etwa 99 Prozent der mit dieser Aufgabe erstmalig Konfrontierten sind der Meinung, dass das Auto ebenso gut hinter der einen wie der anderen Tür stehen kann, und fast 90 Prozent entscheiden sich angesichts dieser vermeintlichen Sachlage dafür, bei der ursprünglichen Tür zu bleiben.
Doch das Ziegenproblem gilt nicht umsonst als »Königin der Denk-Illusionen«. Die richtige Antwort lautet: Es ist besser, die Tür zu wechseln. Sirena und Norbert haben die korrekte Lösung gefunden.
Die mathematische Lösung wurde durch verschiedene Experimente nachgewiesen worden. Am schnellsten geht das natürlich durch Simulation am Computer.
Falls du Sirena und Norbert noch nicht glaubst, kannst selbst testen, indem du eine Strategie wählst und das Experiment häufig (mindestens 20-mal) durchführst:
10 Varianten des Ziegenproblems - Gefangenenproblem
Problem der drei Gefangenen:

Drei Verurteilte sitzen in der Todeszelle. Die Hinrichtung ist auf den nächsten Tag zur Mittagszeit angesetzt. Am Morgen des schwarzen Tages flüstert ihnen ein Wärter zu: ,,Der König hat einen von euch begnadigt! Ich darf aber nicht verraten, wer es ist - es könnte mich den Kopf kosten."
Der Gefangene A gibt sich damit nicht zufrieden. Er lässt sich zum Anstaltspfarrer führen. Auf dem Weg zum Seelsorger steckt er dem Wärter ein Goldstück zu und bittet ihn: ,,Gib wenigstens einen Hinweis!" Der windet sich weiter: ,,Ich darf dir nicht sagen, wie es um dich steht." A lässt nicht locker, es brauche ja nur ein indirekter Hinweis zu sein. Der Wärter wird schließlich mürbe:,,Na gut, wer begnadigt ist, darf ich dir nicht sagen, aber eins kann ich wohl verraten: B muss sterben!"
A denkt: ,,Erst lagen meine Chancen bei , jetzt sind sie immerhin auf gestiegen."
Ist er zu Recht erleichtert?
Die vorliegenden vier Fälle sind nicht gleichwahrscheinlich:

Im Baumdiagramm ist die erste Stufe das "Begnadigen", die zweite Stufe ist das "Nennen" durch den Wärter.
Mit dem Satz von Bayes kann man die Wahrscheinlichkeit für A berechnen:
Es hat sich für A also nichts an der Wahrscheinlichkeit geändert.
Aber für C hat sich die WKT auf erhöht:
11 Varianten des Ziegenproblems - Spiel mit drei Karten

Es wird mit drei Karten gespielt: Eine ist beidseitig weiß, die andere beidseitig rot, und die dritte Karte hat eine rote und eine weiße Seite. Die Karten liegen verhüllt unter einem Tuch. Jetzt darfst du, allerdings ohne unter das Tuch zu sehen, eine der Karten hervorholen und sie auf den Tisch legen.
Du siehst eine weiße Kartenseite. Willst du nun darauf wetten, dass die andere Seite der Karte rot gefärbt ist?
Diesmal denken wir vorher:
Die Wahrscheinlichkeit, dass die beidseitig rote Karte gezogen wird, beträgt . (Das kann aber hier nicht vorliegen, da du weiß siehst.)
Die Wahrscheinlichkeit, dass die rot-weiße Karte gezogen wurde, ist . Allerdings muss auch die weiße Seite oben liegen. Die Karte hat damit die Wahrscheinlichkeit .
Die Wahrscheinlichkeit, dass die beidseitig weiße Karte gezogen wurde, ist .
Du solltest also nicht darauf wetten, dass die andere Seite rot ist, da die Wahrscheinlichkeit dafür nur halb so groß ist, wie die Wahrscheinlichkeit für eine zweite weiße Seite.
