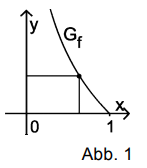
In einem Koordinatensystem (vgl. Abbildung 1) werden alle Rechtecke betrachtet, die folgende Bedingungen erfüllen:
Zwei Seiten liegen auf dem Koordinatenachsen.
Ein Eckpunkt liegt auf dem Graphen der Funktion mit .
Abbildung 1 zeigt ein solches Rechteck.
Unter den betrachteten Rechtecken gibt es eines mit größtem Flächeninhalt. Berechnen Sie die Seitenlängen dieses Rechtecks.