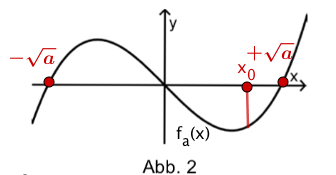
Für jeden Wert von mit ist eine Funktion durch mit gegeben.
a) (2 BE) Einer der beiden Abbildungen stellt einen Graphen von dar. Geben Sie an, für welche Abbildung dies zutrifft. Begründen Sie Ihre Antwort.
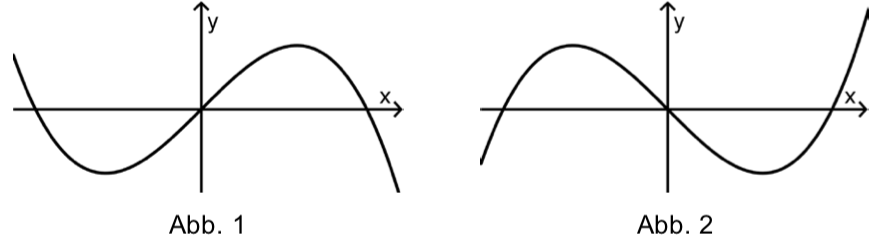
b) (3 BE) Für jeden Wert von besitzt der Graph von genau zwei Extrempunkte. Ermitteln Sie denjenigen Wert von , für den der Graph der Funktion an der Stelle einen Extrempunkt hat.