Teilaufgabe a)
Aus der Aufgabenstellung sind 3 Arbeitsaufträge herauszulesen:
Stelle die Geradengleichung durch und auf
Zeige, dass sowohl auf Gerade als auch auf Gerade liegt
Weise nach, dass die beiden Geraden aufeinander senkrecht stehen
ist Ursprungsgerade mit der Gleichung
Wer sich streng an das Aufstellen einer Geradengleichung bei vorgegebenen 2 Punkten hält, der setzt an:
Es ist notwendig, dass die zweite Gerade eine andere Parameterbezeichnung - hier ist es - erhält, sonst gibt es beim Aufstellen von Gleichungen und Suchen von Schnittpunkten große Probleme, weil man Terme zusammenfasst, die dafür nie vorgesehen waren.
Aber hier geht es etwas einfacher, denn der Schnittpunkt ist schon bekannt und man muss nur zeigen, dass sich zu bei der Geraden eindeutig (also widerspruchsfrei) ein finden lässt und bei der Geraden entsprechend eindeutig ein !
ist also tatsächlich Schnittpunkt von und :
Denn mit dem Ansatz
ergeben sich 3 Gleichungen:
Gleichungen I und III werden jeweils - widerspruchsfrei - durch gelöst. Gleichung II ist allgemeingültig und somit immer erfüllt.
Entsprechend findet man, dass für .
Daher gilt insgesamt: .
steht senkrecht auf :
Zwei Geraden schneiden sich senkrecht, wenn sie außer der Existenz des Schnittpunkts auch noch zueinander senkrecht stehende Richtungsvektoren haben. Dies weist man nach, indem man zeigt, dass das Skalarprodukt der beiden Richtungsvektoren Null ist:
Es folgt die Behauptung der Teilaufgabe a. Die Geraden und schneiden sich also senkrecht im Punkt .
Teilaufgabe b)
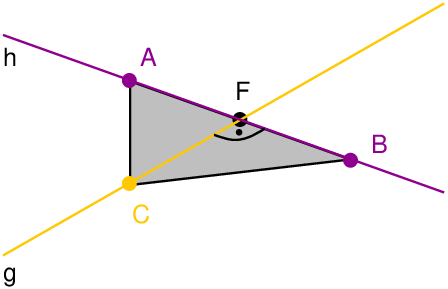
Zur Lösung der Aufgabe ist es am besten, wenn man eine kleine Skizze anfertigt:
Dann erkennt man sofort: ist im Dreieck die Höhe zur Grundlinie , da die Strecke immer senkrecht auf der Grundlinie steht, weil die Gerade senkrecht auf der Geraden steht.