Aufgaben zum Baumdiagramm
- 1
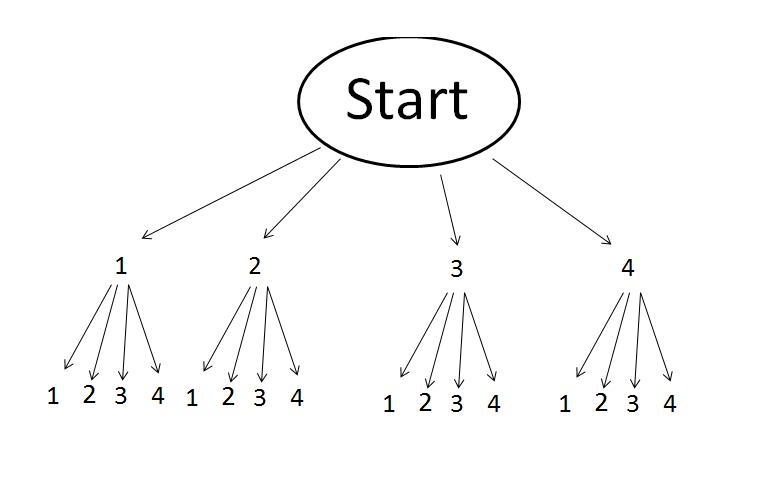
Wie viele zweistellige Zahlen lassen sich aus den Ziffern 1, 2, 3, 4 bilden?
- 2
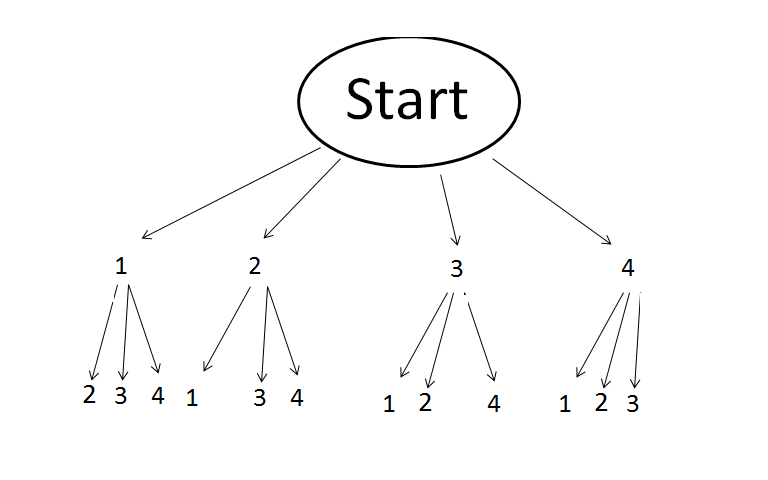
Wie viele zweistellige Zahlen lassen sich aus den Ziffern 1, 2, 3, 4 bilden, wenn keine Ziffer doppelt vorkommen darf?
- 3
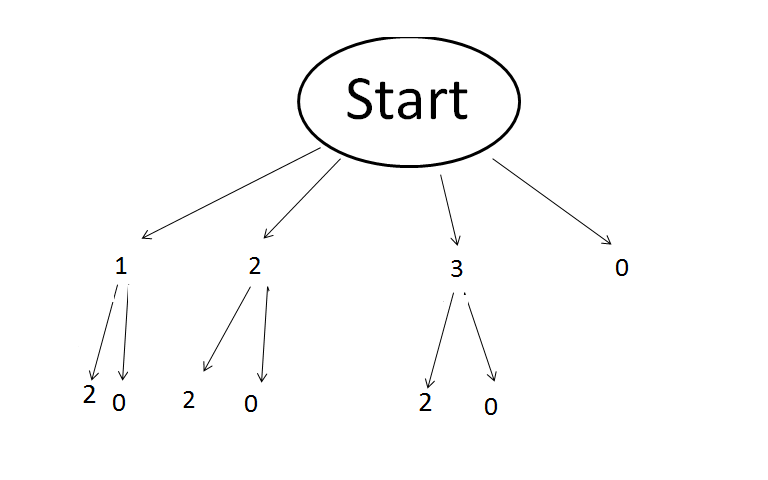
Wie viele gerade zweistellige Zahlen lassen sich aus den Ziffern 0, 1, 2, 3 bilden?
- 4
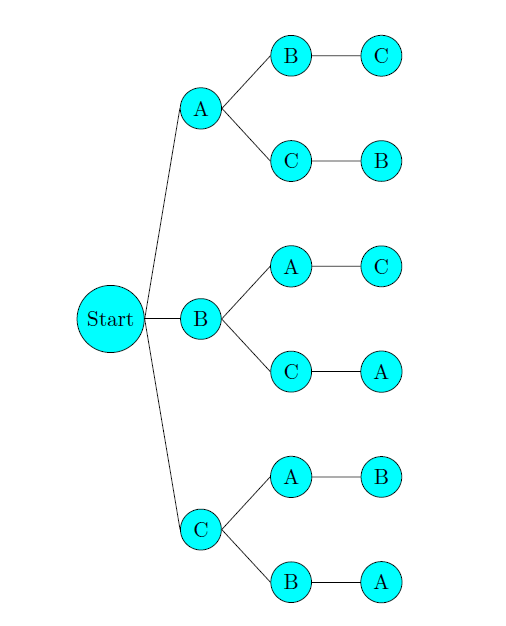
Lucia feiert ihren 11. Geburtstag. Sie hat Angelika (A), Boris (B) und Christoph (C) eingeladen. Sie kommen nacheinander. Bestimme anhand eines Baumdiagramms, wie viele und welche Möglichkeiten ihres Eintreffens es gibt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?