Aufgaben zur relativen Häufigkeit
- 1
Würfle 100-mal und bestimme die relative Häufigkeit der Augenzahl 6 für
die ersten 20,
die zweiten 20,
die dritten 20,
die vierten 20 und
die fünften 20 Würfe.
- 2
Bei einer Schulaufgabe ergab sich für die Noten folgende Verteilung:
Note
1
2
3
4
5
6
Anzahl
3
2
9
6
7
2
Berechne die relative Häufigkeit der einzelnen Noten!
- 3
In einer Schulklasse sind 28 Schüler, darunter 12 Mädchen. Bei einer Umfrage gaben 7 Mädchen und 8 Buben an, Sport sei ihr Lieblingsfach.
Ist das Fach Sport laut der Umfrage bei den Mädchen oder bei den Jungen in der Klasse beliebter?
- 4
Als Hausaufgabe sollten die Schüler der Klasse 6 b mindestens 100-mal würfeln und die relativen Häufigkeiten, mit denen die einzelnen Augenzahlen aufgetreten sind, mithilfe einer Tabelle oder eines Diagramms darstellen.
Am nächsten Tag vergleichen Manfred, Peter, Klaus und Christian ihre Ergebnisse:
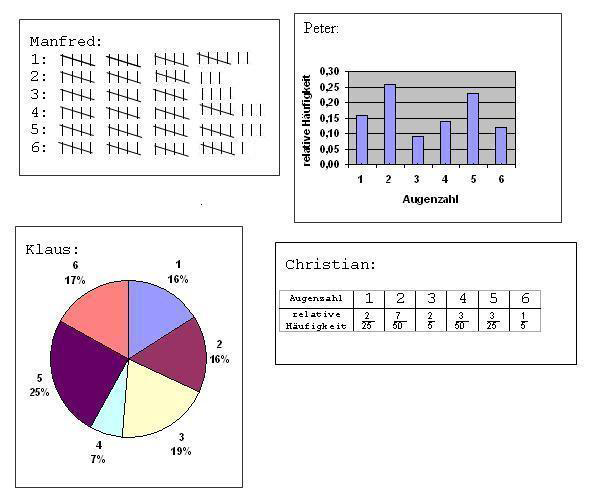
Nach einem kurzen Blick in Manfreds Heft sagt Christian: „Du hast wohl in der letzten Mathestunde nicht richtig aufgepasst!“ Wie kommt er dazu?
Klaus hat genau 200-mal gewürfelt. Wie oft hat er eine „6“ geworfen?
MalPeter betrachtet kurz die Diagramme und verkündet dann laut: „Christian hat von uns vier den besten Würfel. Bei ihm fällt am häufigsten die Sechs.“ Wie kommt Peter zu dieser Aussage? Glaubst auch du, dass Christian den besten Würfel hat?
- 5
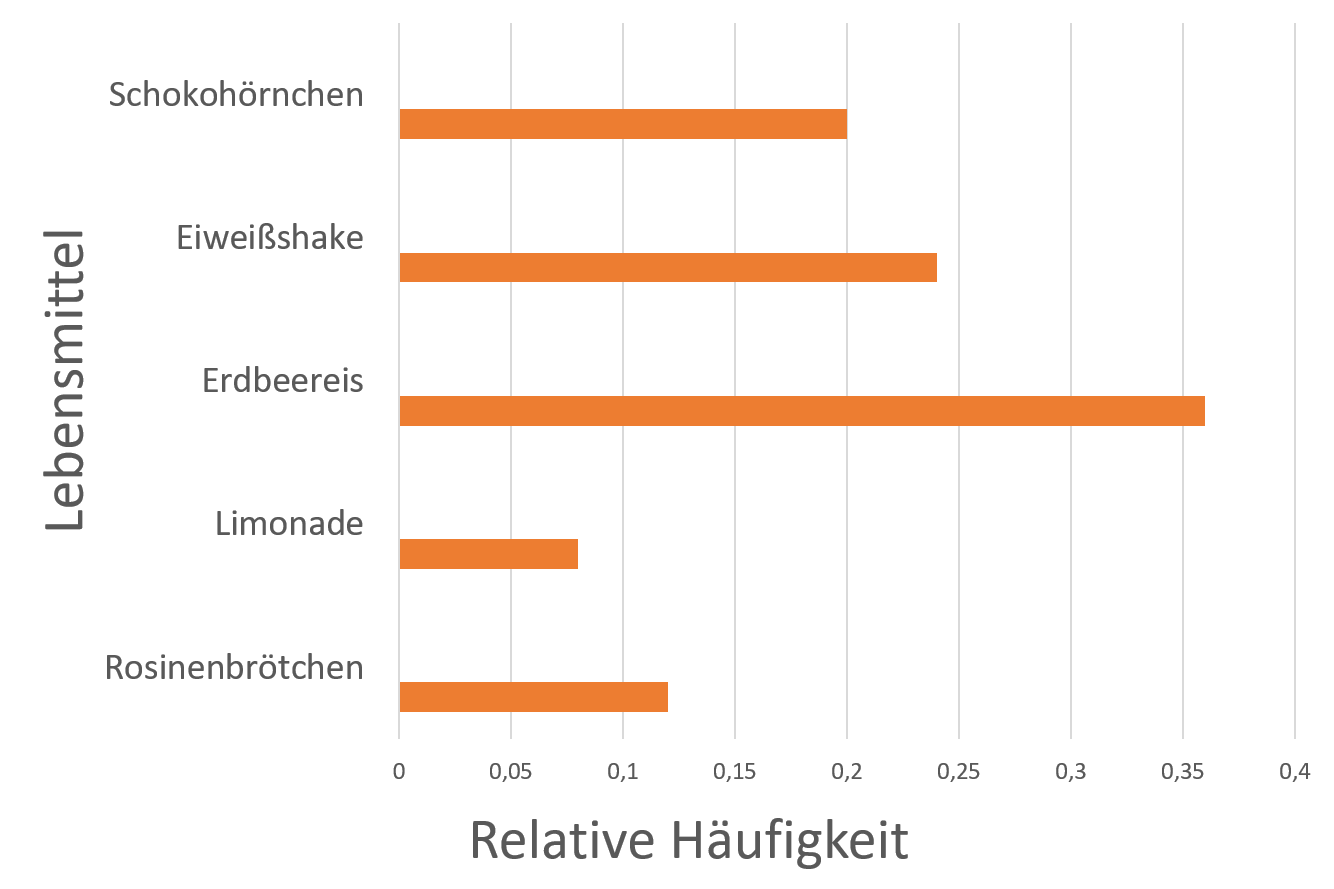
Marie und Lukas startet einen Umfrage in der Schule. Es geht darum, welches Lebensmittel noch im Schulkiosk angeboten werden soll. Sie befragen insgesamt 50 Schülerinnen und Schüler. Wenn die beiden die Umfrage richtig auswerten und schön präsentieren, wird das gewünschte Lebensmittel im Kiosk angeboten. Das Ergebnis ist folgendes:
Schokohörnchen
Eiweißshake
Erdbeereis
Limonade
Rosinenbrötchen
10
12
18
4
6
Hilf den beiden die relative Häufigkeit zu bestimmen und in einem Balkendiagramm anschaulich zu präsentieren.
- 6
Aus den abgebildeten Netzen lassen sich „Spielwürfel“ mit und Seitenflächen erstellen.
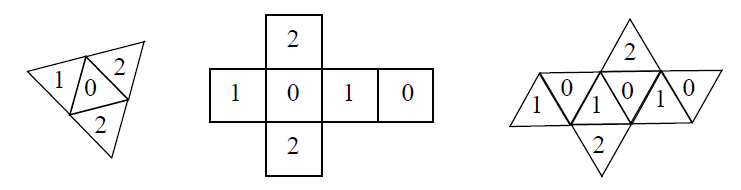
Welche Wahrscheinlichkeiten erhältst du für die Augenzahlen und bei den verschiedenen „Spielwürfeln“, wenn du sehr oft würfelst?
Bei einem Spiel würfelt jeder Teilnehmer so lange, bis er zum ersten Mal eine „“ geworfen hat. Wer am wenigsten Würfe benötigt, gewinnt. Welchen Würfel würdest du für dieses Spiel auswählen? Erläutere deine Entscheidung.
Bei einem anderen Spiel wird reihum gewürfelt. Wer eine „“ würfelt, scheidet aus. Wie groß ist mit den verschiedenen Würfeln jeweils die Chance, bei einem Wurf keine „“ zu werfen?
Bei tausend Würfen mit einem der drei Würfel hat sich folgendes Ergebnis ergeben:
Augenzahl
0
1
2
absolute Häufigkeit
241
253
506
Was meinst du, welcher Würfel verwendet wurde? Erläutere deine Antwort.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?