Aufgaben zum graphischen Differenzieren
Hier findest du Aufgaben zum graphischen Differenzieren. Übe, die Ableitung eines Graphen darzustellen und einzuzeichnen.
- 1
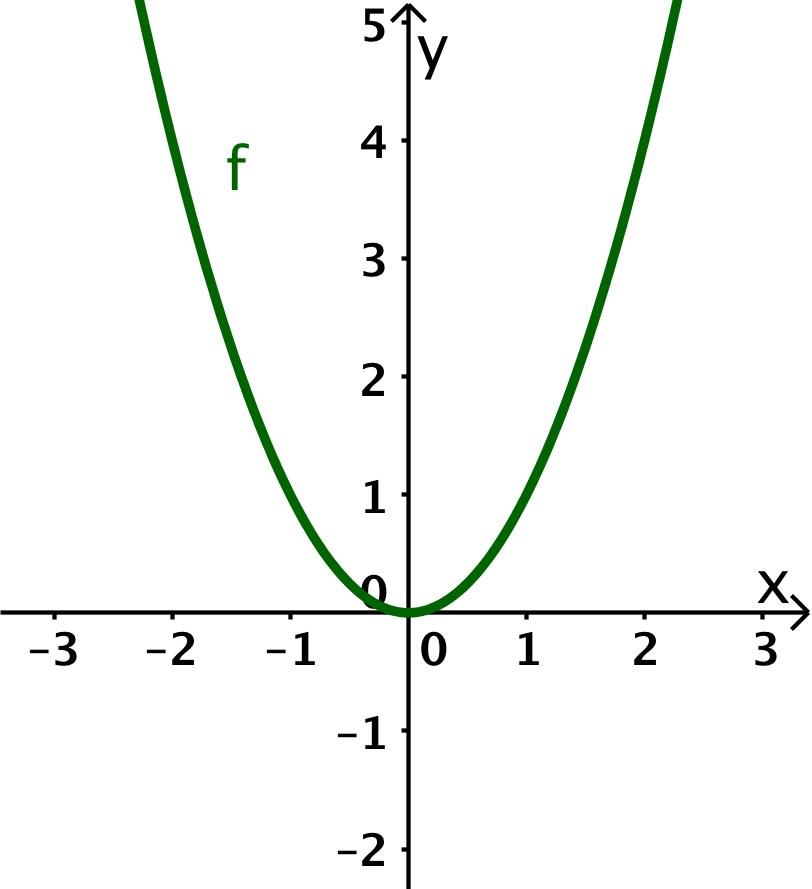
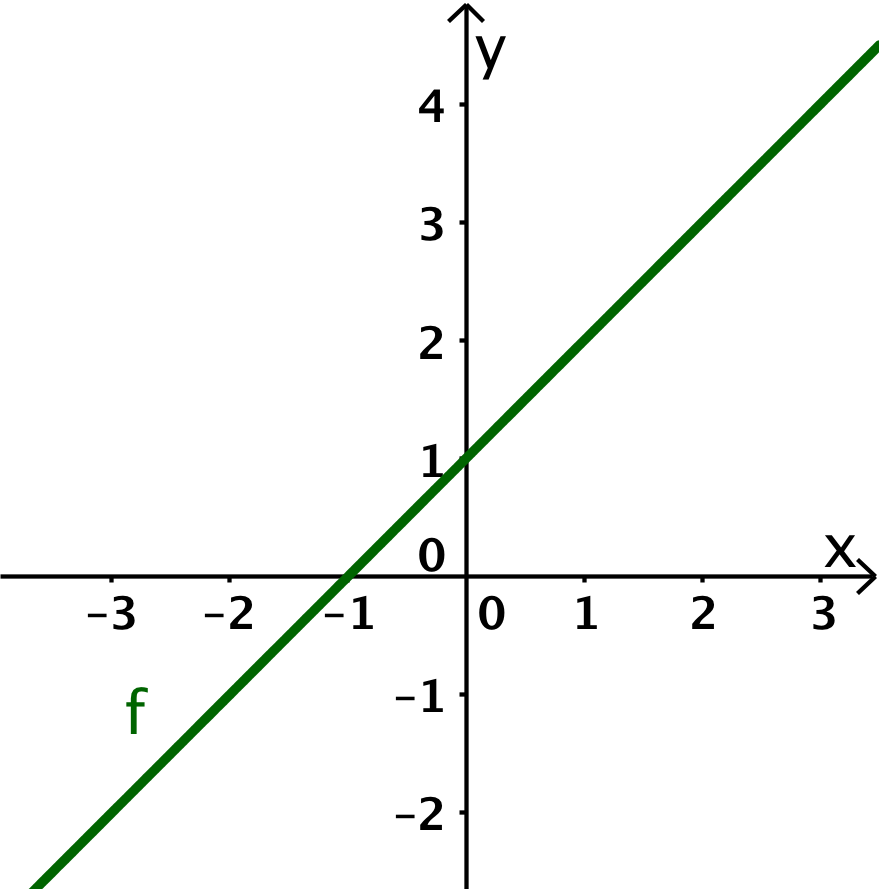
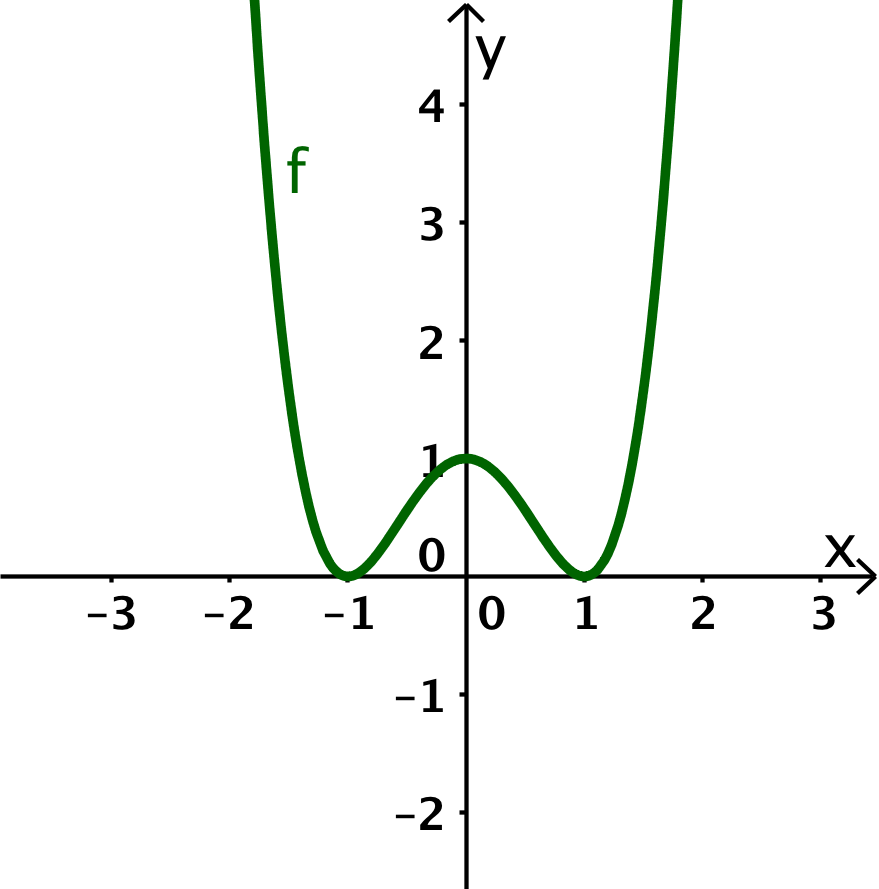
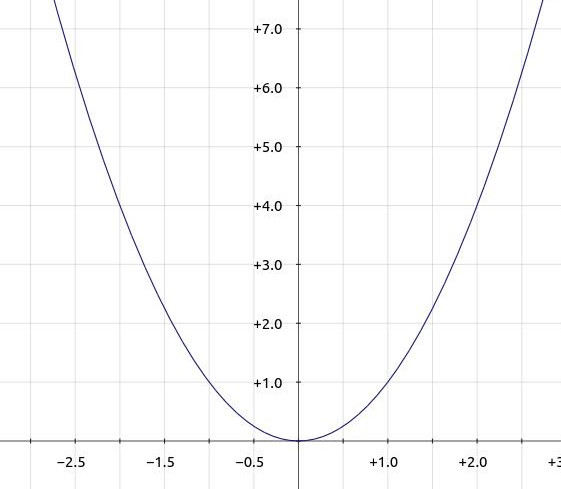
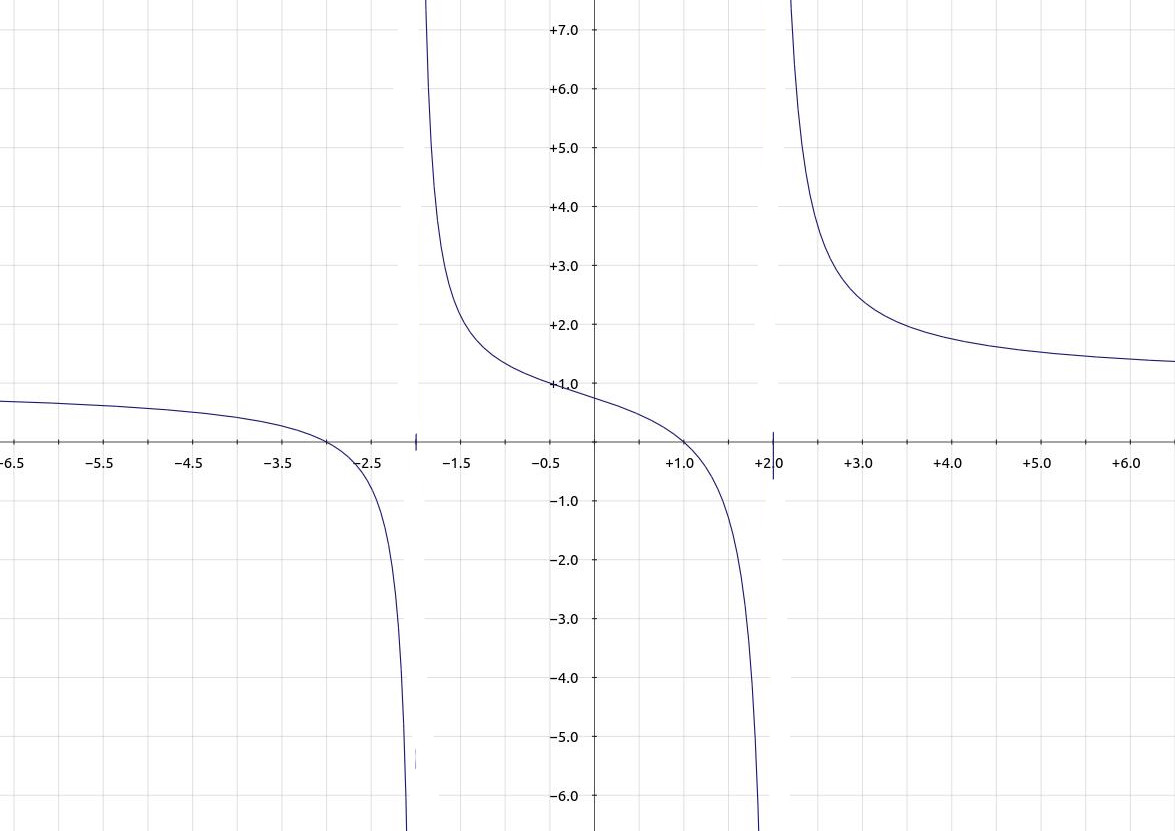
Skizziere zu den folgenden gegebenen Graphen den Graph der zugehörigen Ableitung.
- 2
(frei nach einer Abituraufgabe von 2012)
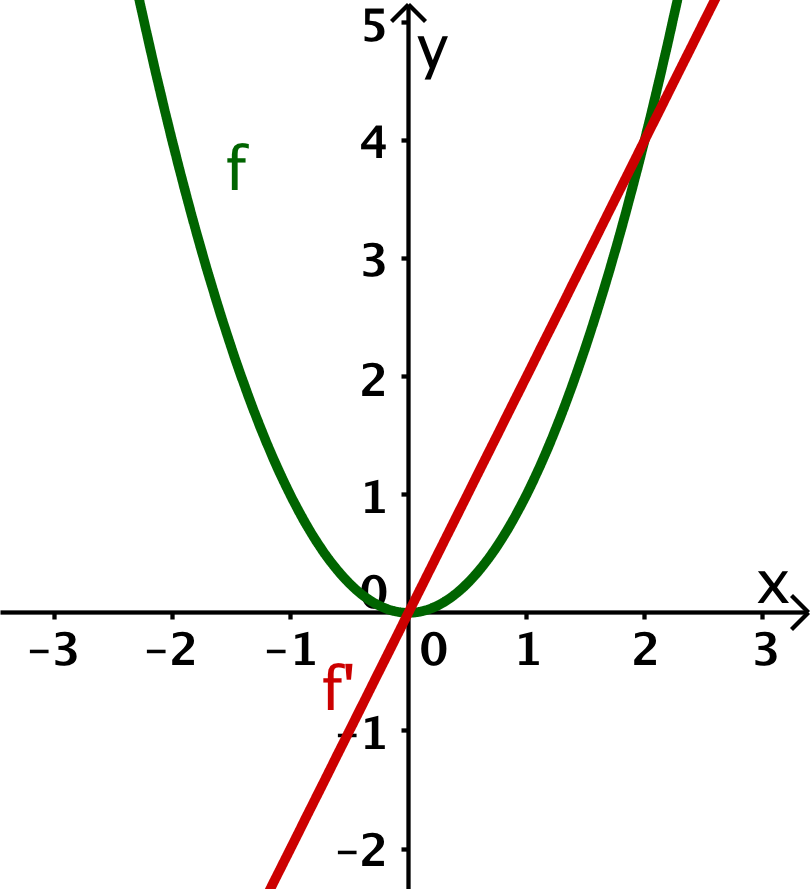
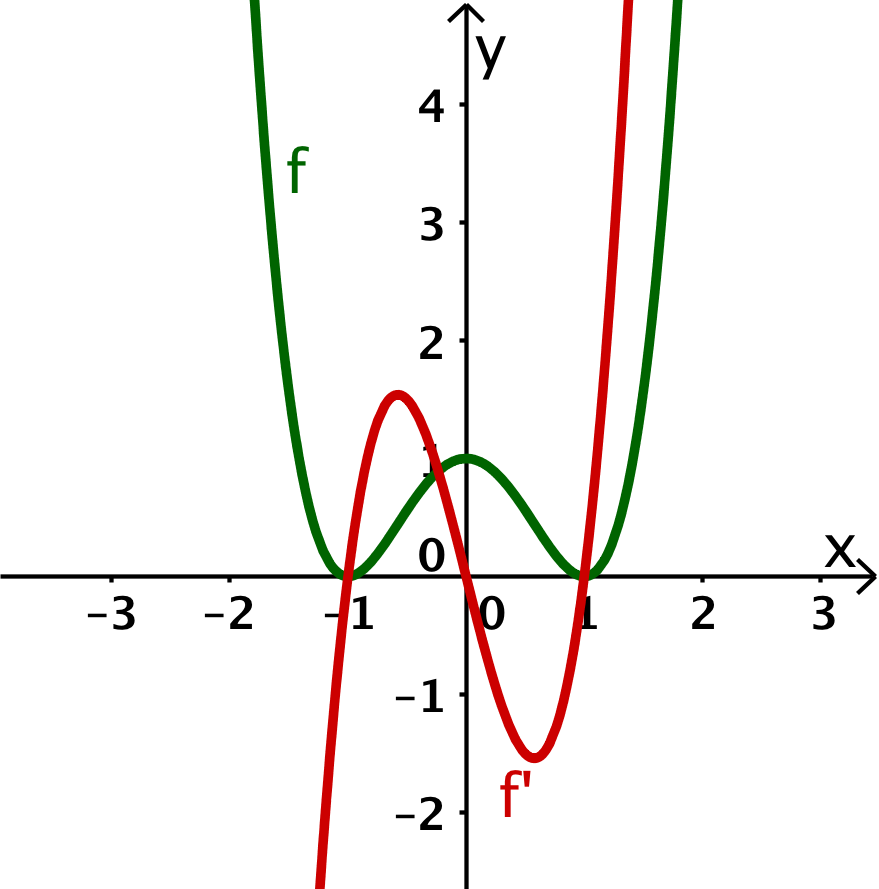
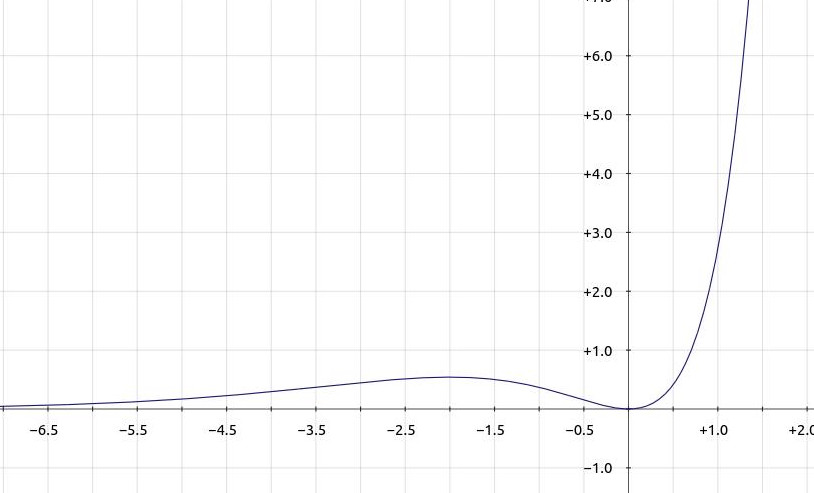
Die Abbildung zeigt dir den Graphen der Funktion . Skizziere den Graphen der zugehörigen Ableitungsfunktion möglichst genau.
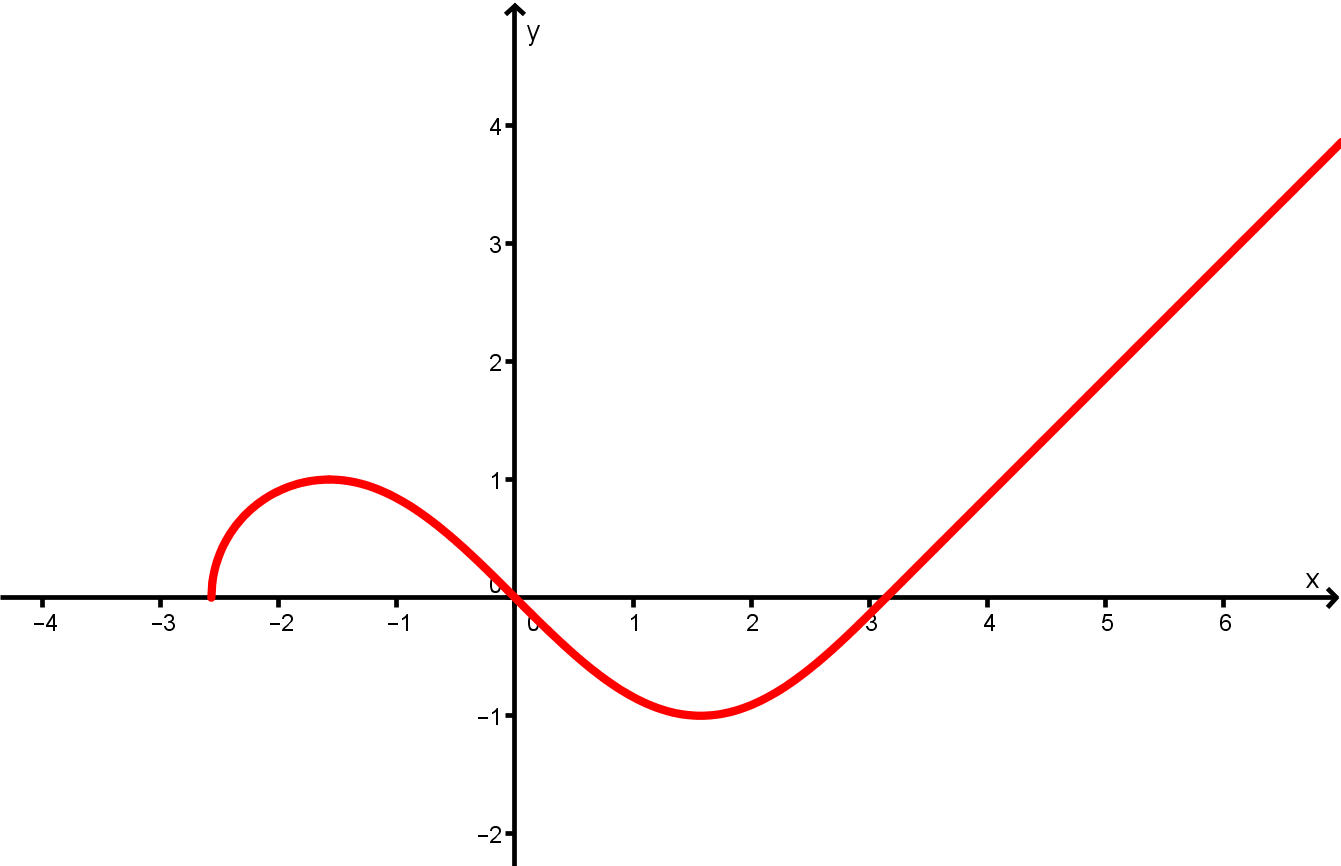
- 3
Grafisches Skizzieren der Ableitung mit Video-Lösung
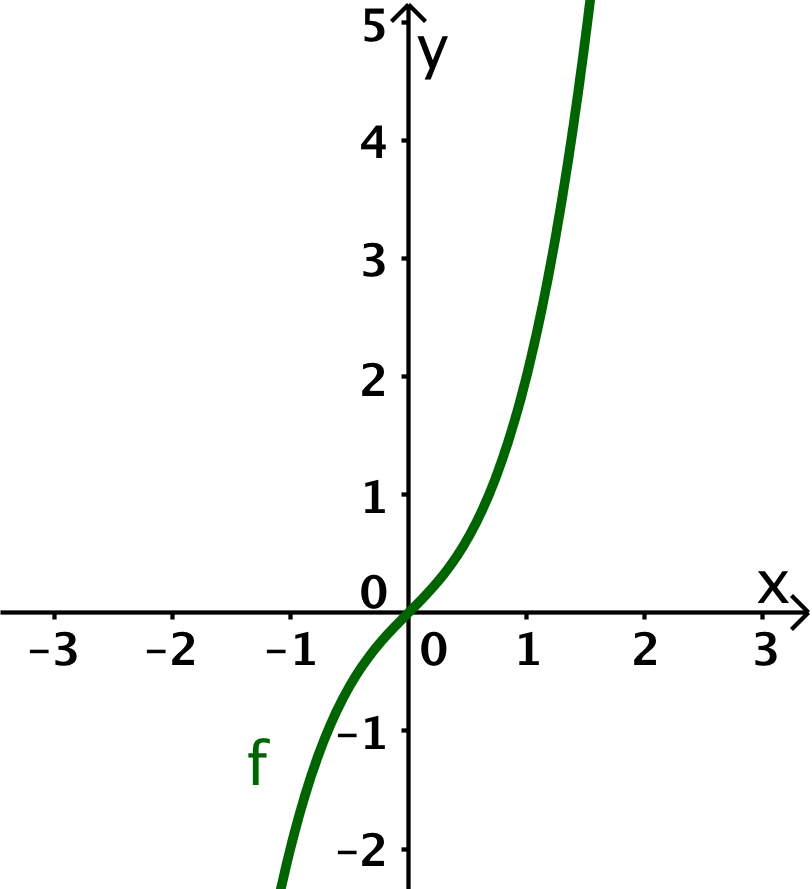
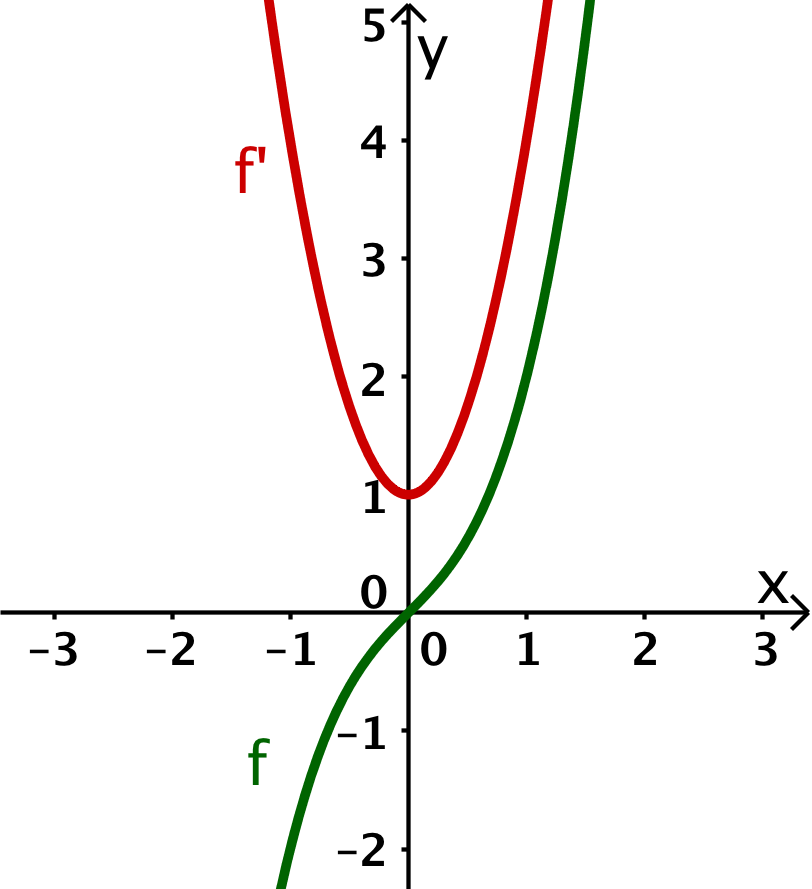
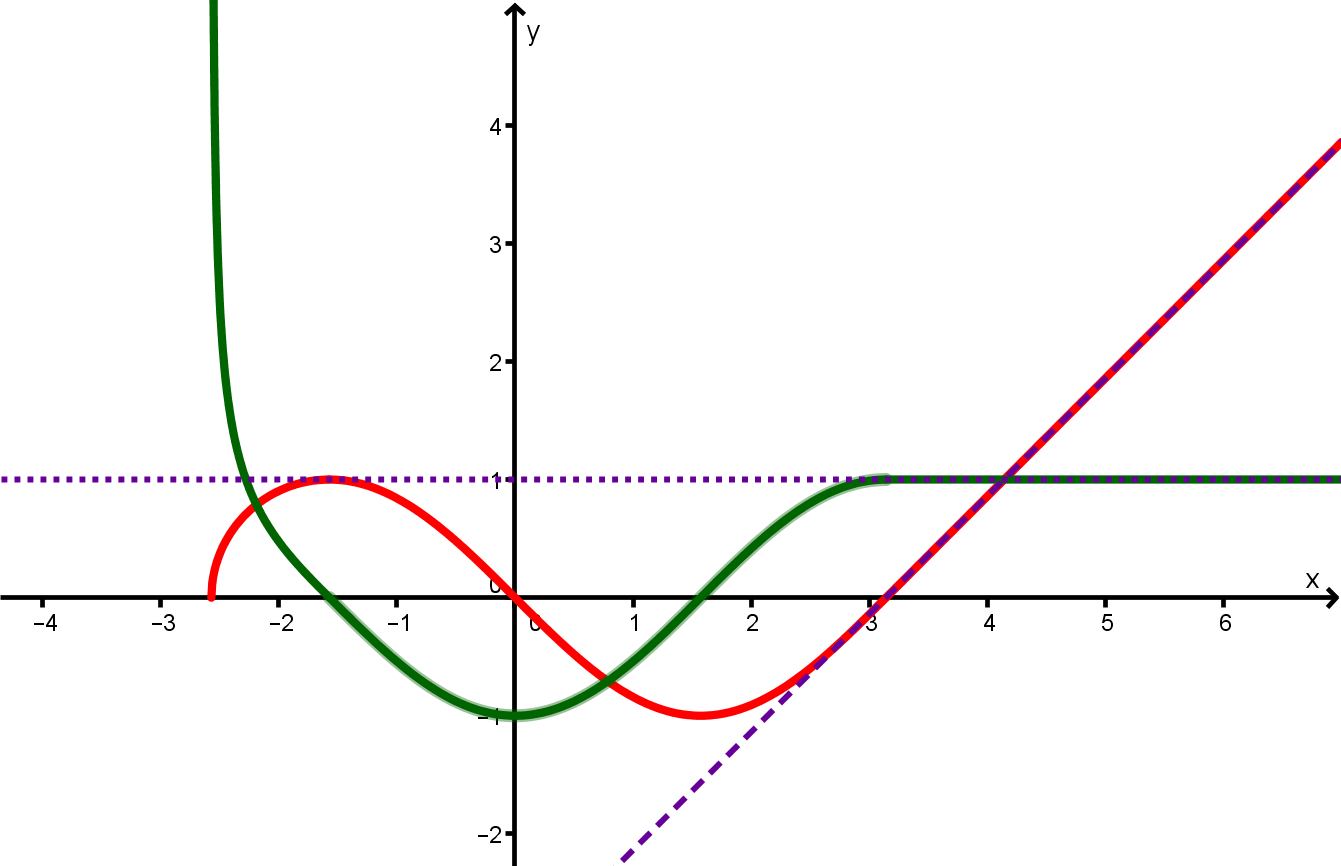
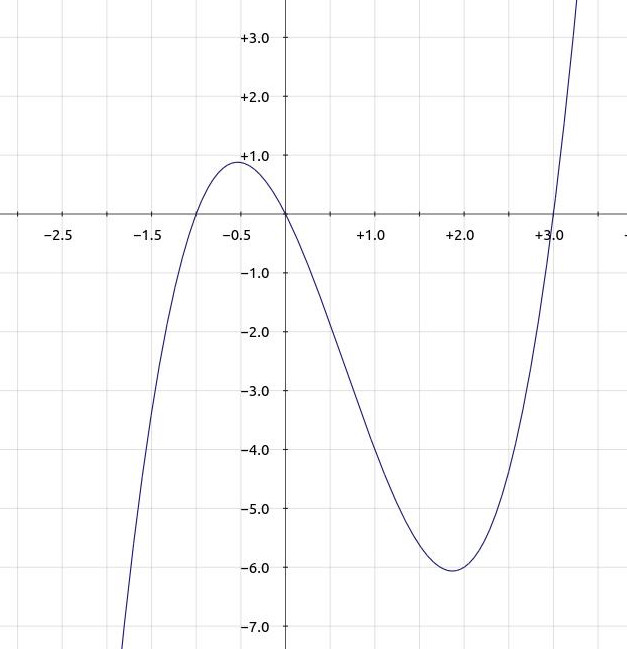
Übertrage die folgenden Graphen in dein Heft. Genaue Werte sind nicht wichtig. Male mit Schwung die Kurve und überlege dann wie der Graph der Ableitung aussehen könnte.
- 4
Interaktive Aufgaben zum graphischen Ableiten auf KMap ..
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?