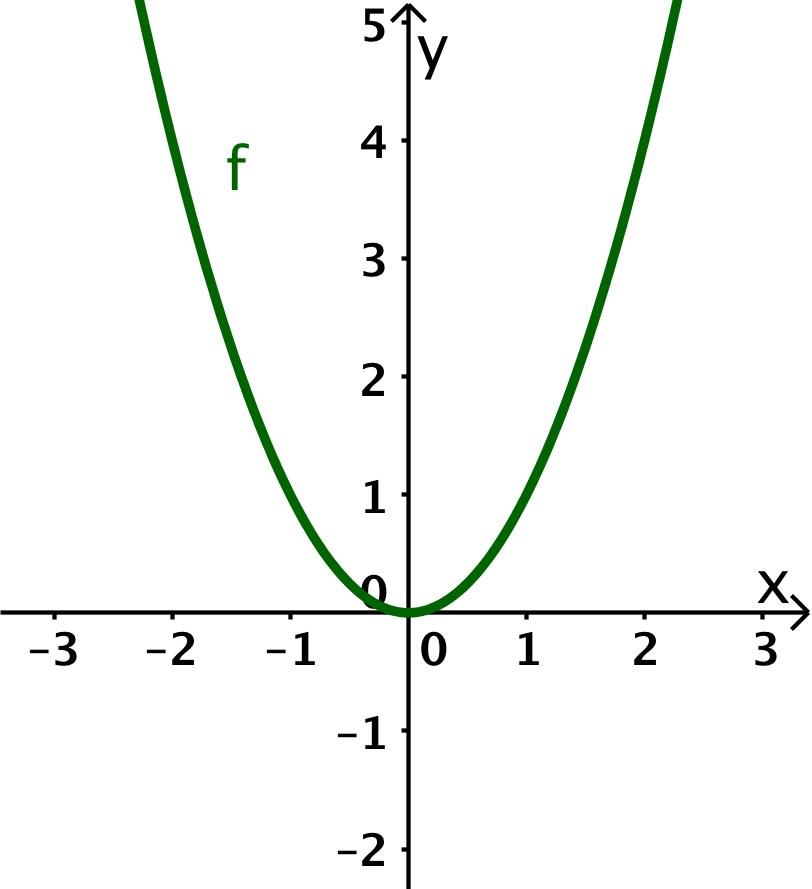
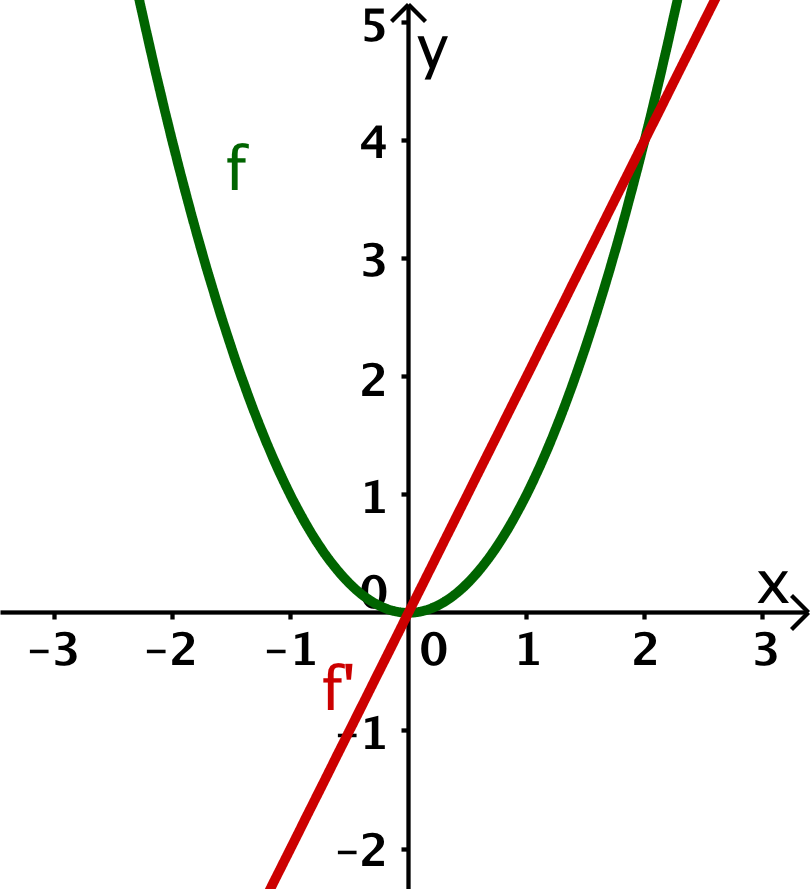
Der Graph von $ff$ hat an $x=0x=0$ ein lokales Minimum. Das bedeutet, dass der Graph der Ableitung an $x=0x=0$ die $xx$-Achse von unten nach oben durchschreitet.

Zudem fällt der Graph von $ff$ für und daher ist der Graph von $f^{\mathrm{\prime }}f\text{'}$ dort kleiner als $00$.

Weiterhin steigt der Graph von $ff$ für $x>0x>0$ und daher ist der Graph von $f^{\mathrm{\prime }}f\text{'}$ dort größer als $00$.

Aus diesen Gründen ergibt sich der Graph der Ableitung wie im Bild rechts.

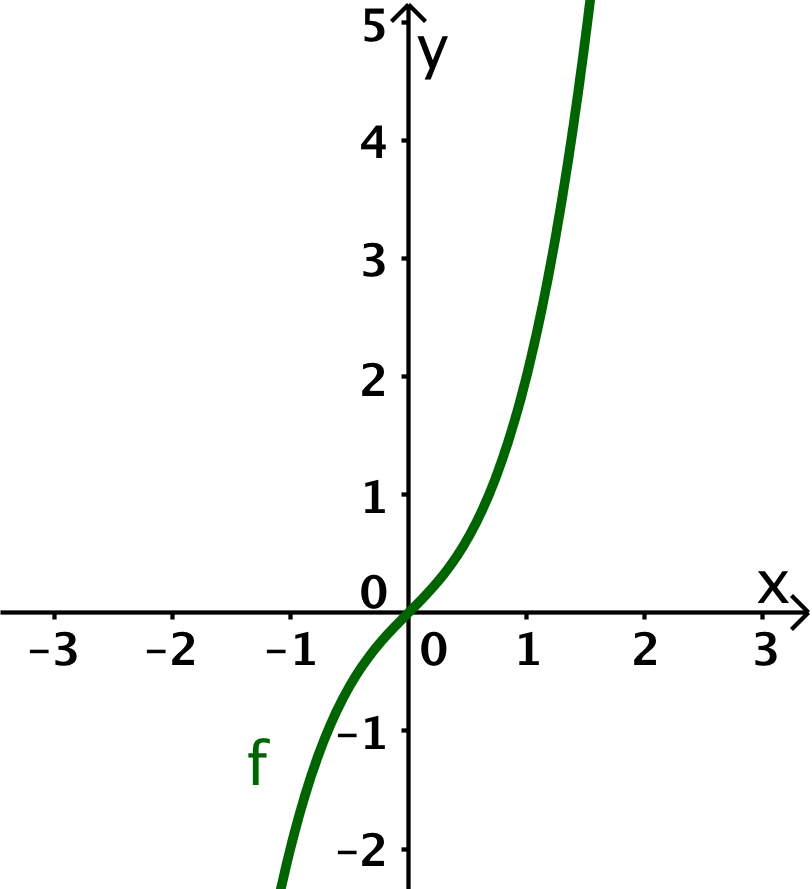
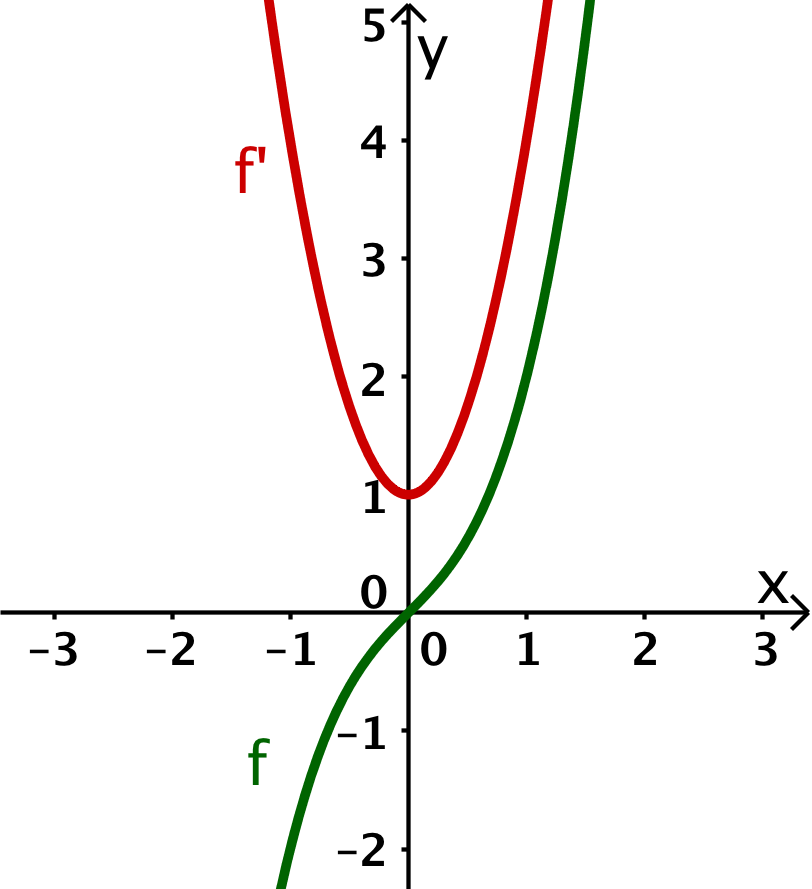
Da der Graph von $ff$ überall positive Steigung hat, befindet sich der Graph von $f^{\mathrm{\prime }}f\text{'}$ über der $xx$-Achse.

Der Graph von $ff$ ist weiterhin eine ungerade Funktion, weshalb der Graph von $f^{\mathrm{\prime }}f\text{'}$ gerade ist.

Die Steigung des Graphen von $ff$ nimmt für $x\to \mathrm{\infty }x\; \backslash to\; \backslash infty$ und $x\to -\mathrm{\infty }x\; \backslash to\; -\backslash infty$ zu, weshalb die Werte von $f^{\mathrm{\prime }}f\text{'}$ zunehmen.

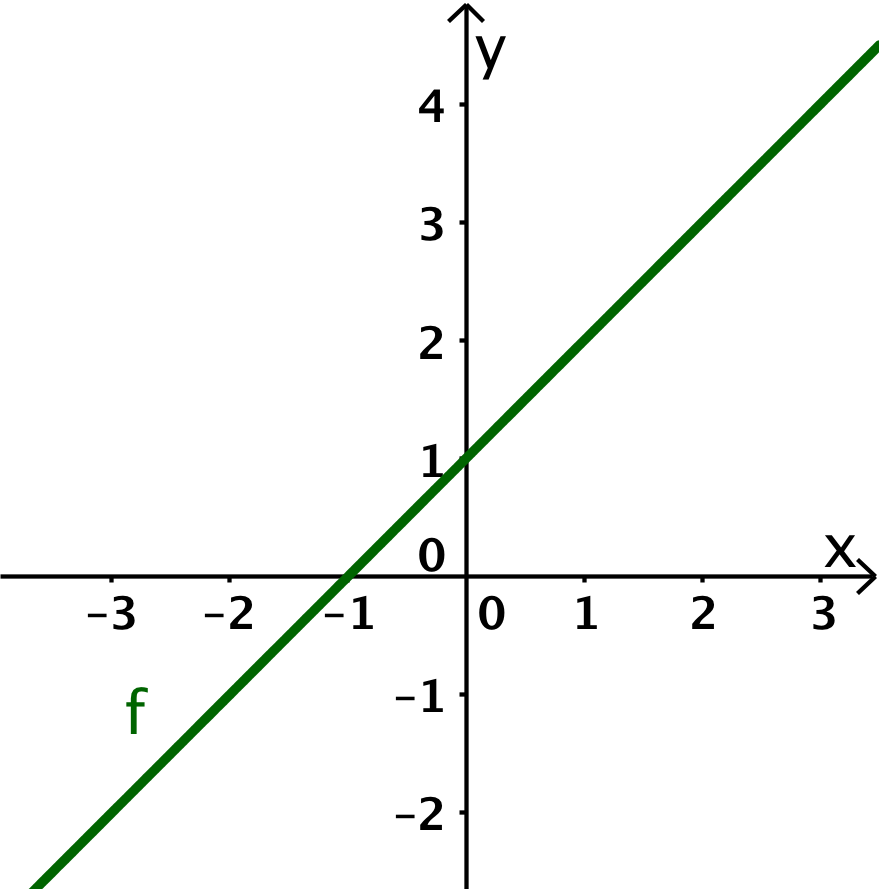
Der Graph von $ff$ stellt eine Gerade dar. Eine Gerade hat eine konstante Steigung. Der Graph von $f^{\mathrm{\prime }}f\text{'}$ stellt immer die Steigung dar, weshalb hier der Graph von $f^{\mathrm{\prime }}f\text{'}$ eine Konstante ist.

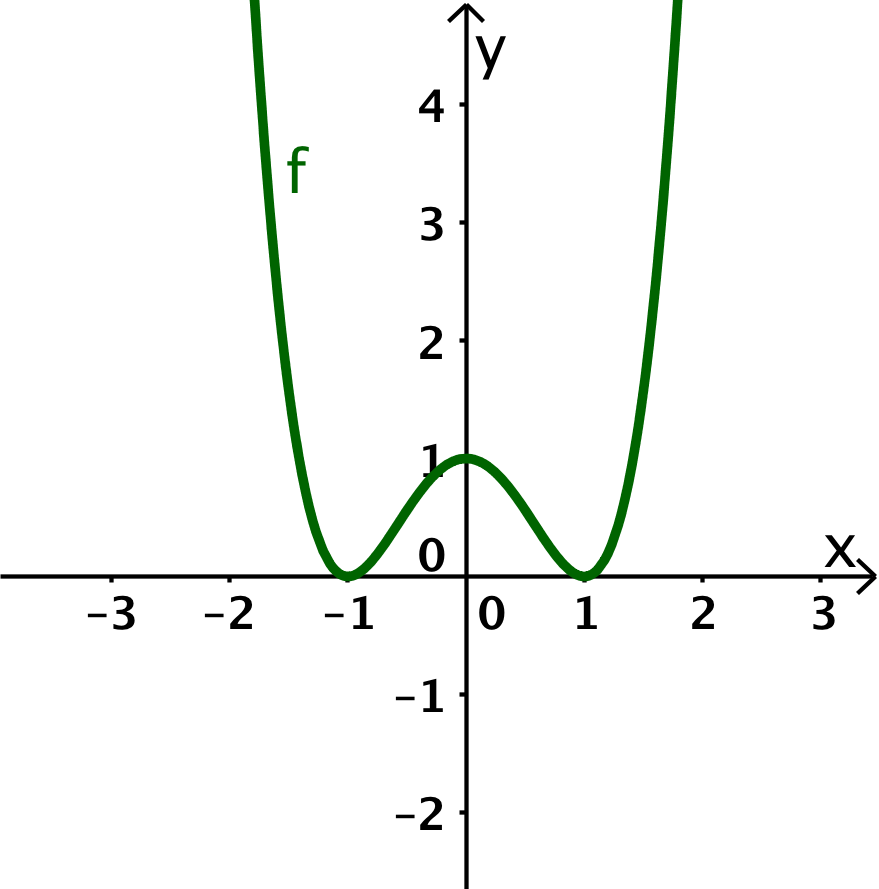
Die Funktion $ff$ besitzt 3 Extrema. Dabei sind Minima an $x=-1,x=1x=-1,\; x=1$ und Maxima an $x=0x=0$.

• Minima: Der Graph von $f^{\mathrm{\prime }}f\text{'}$ an $x=-1x=-1$ und $x=1x=1$ die $xx$-Achse von unten nach oben.

• Maxima: Der Graph von $f^{\mathrm{\prime }}f\text{'}$ an $x=0x=0$ die $xx$-Achse von oben nach unten.

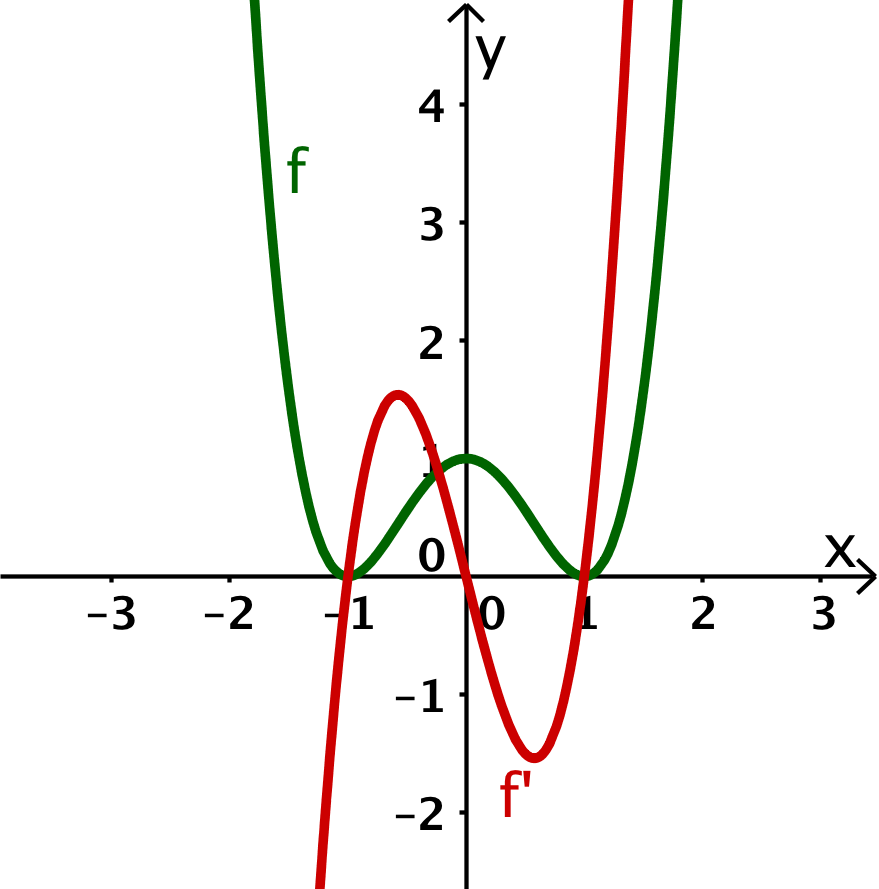
Die Steigung von $ff$ wächst betragsmäßig für $\mathrm{\mid }x\mathrm{\mid }\to \mathrm{\infty }|x|\; \backslash to\; \backslash infty$ und daher nehmen die Funktionswerte von $f^{\mathrm{\prime }}f\text{'}$ zu.

Es ergibt sich ein Graph wie rechts im Koordinatensystem.