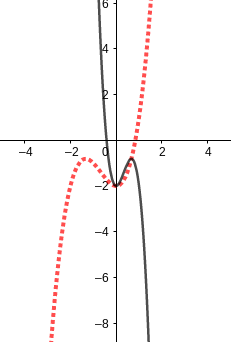
Gegeben ist die Funktion
Gib den Term der Funktion an, wenn die Funktion mit dem Streckungsfaktor in Richtung der -Achse gestreckt wird. Welche Besonderheit ergibt sich aus dem Streckungsfaktor?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?