Aufgaben zur Entstehung der allgemeinen Sinusfunktion
Wie gut kennst du dich mit der Sinusfunktion aus? Mit diesen Aufgaben lernst du die allgemeine Sinusfunktion mit deren Parameter und zu untersuchen.
- 1
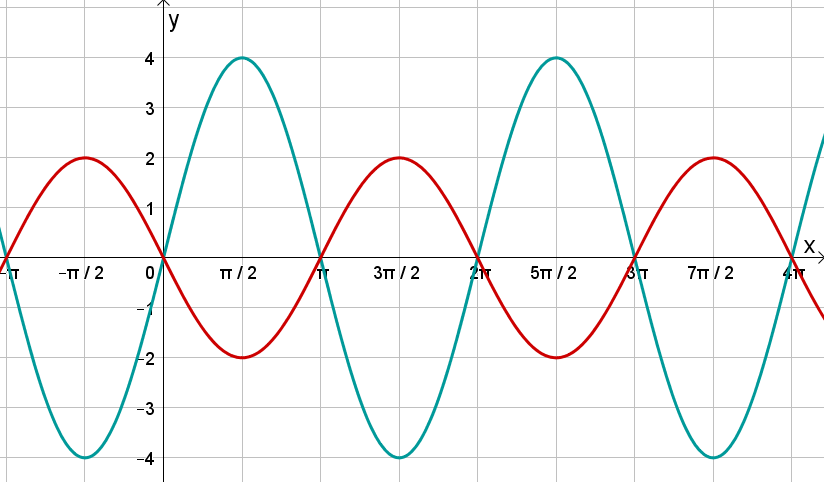
Verändere den Parameter und beobachte, wie sich der Funktionsgraph von , , gegenüber dem Graphen von (hier in schwarz abgebildet) ändert!
Beantworte anschließend die Fragen.
Für
Für
Für
Für
Für
Für
Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
- 2
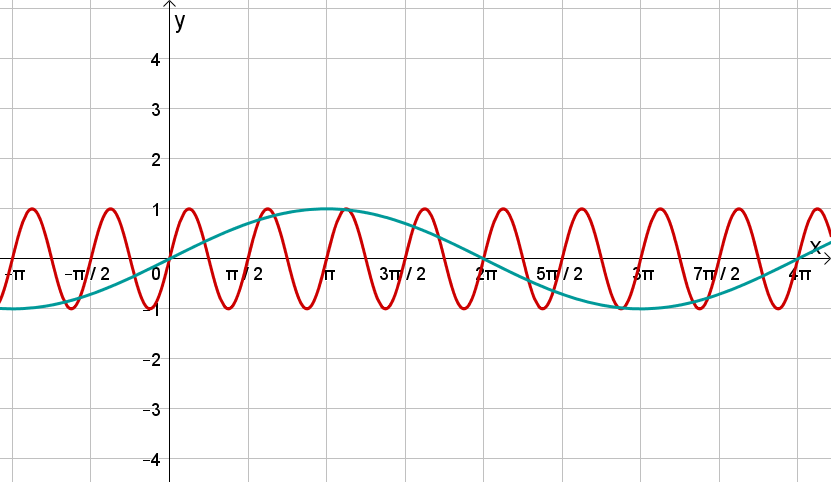
Verändere den Parameter und beobachte, wie sich der Funktionsgraph von , , , gegenüber dem Graphen von (hier in grau abgebildet) ändert!
Beantworte anschließend die Fragen.
Für
Für
Für
Die Periode der Funktion mit der Funktionsgleichung ,
Die Periode der Funktion mit der Funktionsgleichung ,
Die Periode der Funktion mit der Funktionsgleichung ,
Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
- 3
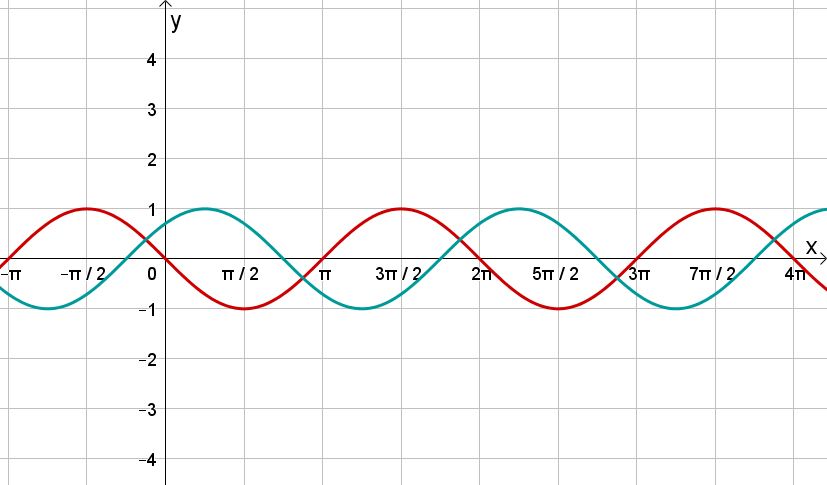
Verändere den Parameter und beobachte, wie sich der Funktionsgraph von , , gegenüber dem Graphen von (hier in grau abgebildet) ändert!
Beantworte anschließend die Fragen.
Für
Für
Für
Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?