Symmetrie zum Koordinatensystem vorhanden
Achsensymmetrie zur -Achse

Beispiel für einen Graphen, der achsensymmetrisch zur -Achse ist.
Jede ganzrationale Funktion, bei der die Variable
nur in Potenzen mit geradem Exponenten vorkommt,
ist achsensymmetrisch zur -Achse.
Punktsymmetrie zum Ursprung
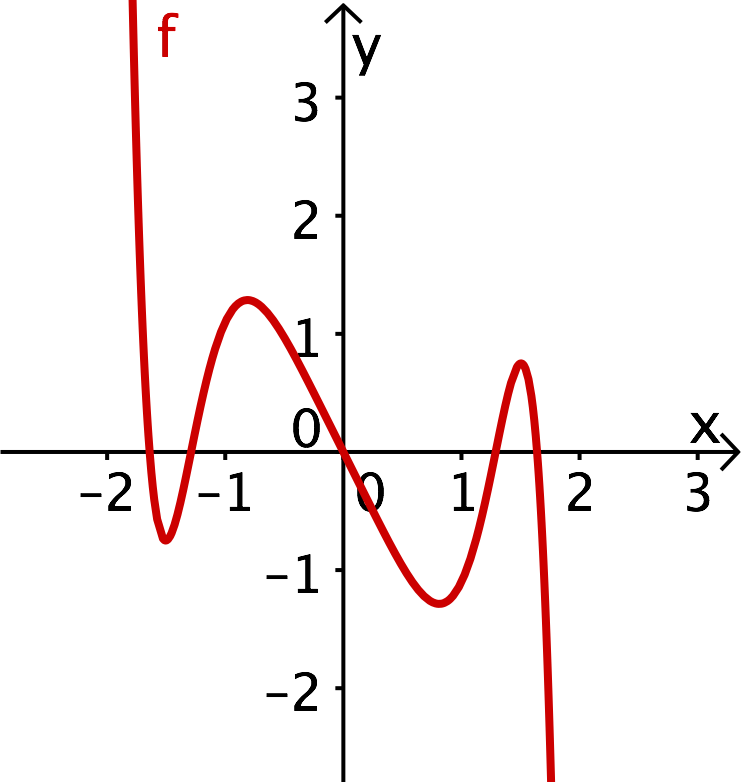
Jede ganzrationale Funktion, bei der die Variable
nur in Potenzen mit ungeradem Exponenten vorkommt,
ist punktsymmetrisch zum Ursprung .
Symmetrie zum Koordinatensystem nicht vorhanden
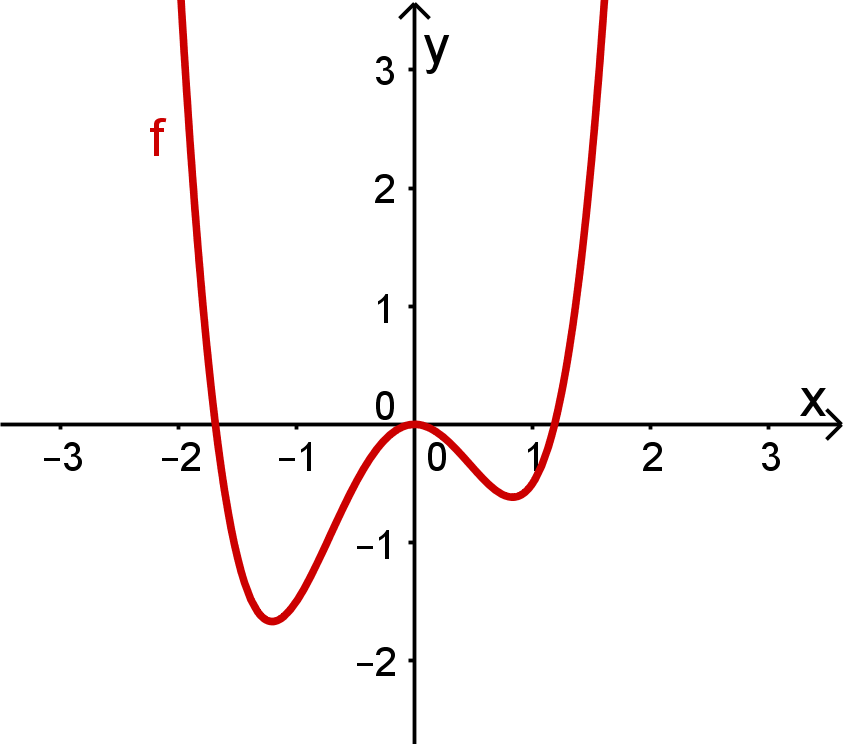
Beispiel für einen Graphen, der keine Symmetrie zum Koordinatensystem aufweist
Wenn in einer ganzrationalen Funktion die Variable
als Potenz mit geradem Exponenten
und außerdem auch
als Potenz mit ungeradem Exponenten vorkommt,
ist der Graph weder achsensymmetrisch zur -Achse noch punktsymmetrisch zum Ursprung.
Ob es Achsensymmetrie zu einer anderen Achse als der -Achse oder Punktsymmetrie zu einem anderen Punkt als dem Ursprung gibt, ist eine andere Frage, die schwieriger zu beantworten ist und hier nicht behandelt werden soll.
