Ebene aus zwei Geraden

Zwei Geraden $g$ und $h$ spannen eine Ebene $E$ auf, wenn sie parallel sind oder sich schneiden.

Mit zwei parallelen Geraden kann die Ebenengleichung in Parameterform durch drei Punkte $A,B,C$ aufgestellt werden, die nicht alle auf der gleichen Geraden liegen.

Die Ebenengleichung ergibt sich zu:

\displaystyle E:~\overrightarrow{x}=\overrightarrow{A}+\lambda\cdot\overrightarrow{AB}+\mu\cdot\overrightarrow{AC}

Vorausgesetzt die Geraden schneiden sich, so reicht es bereits einen Stützvektor einer Gerade zu wählen und die Richtungsvektoren der Geraden als Spannvektoren der Ebene zu übernehmen.

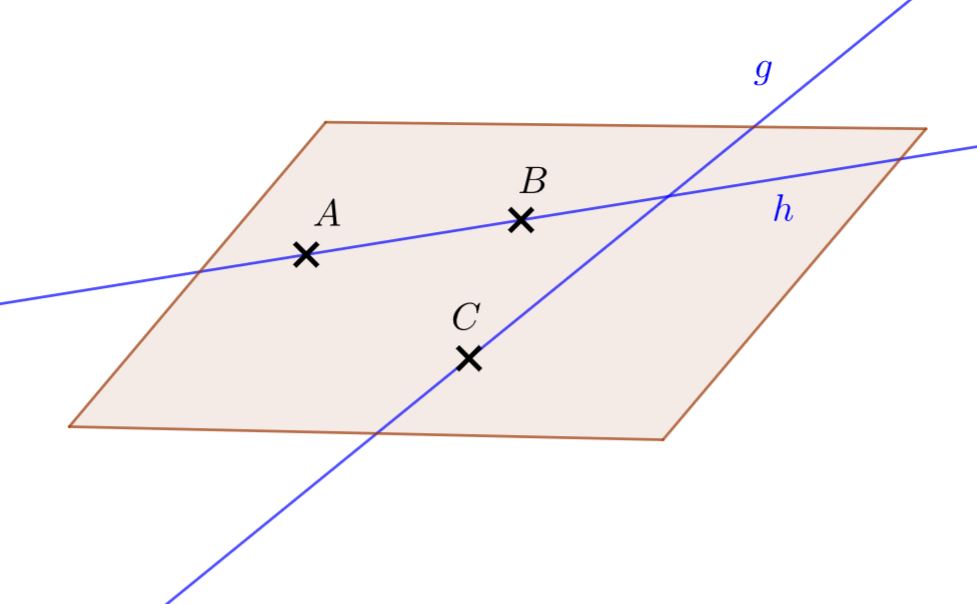
Ebenengleichung aufstellen aus zwei parallelen Geraden

Ausgehend von zwei Geradengleichungen, bspw.

\displaystyle E:~\overrightarrow{x}=\overrightarrow{A}+\lambda\cdot\overrightarrow{AB}+\mu\cdot\overrightarrow{AC}

lassen sich drei Punkte bestimmen, die nicht alle in derselben Geraden enthalten sind. Hierzu werden direkt die Aufpunkte $A(2|3|-1)$ und $B(5|-2|0)$ aus den Stützvektoren entnommen. Für den dritten Punkt wird in der Gerade $h$ , $t=1$ gesetzt:

\displaystyle E:~\overrightarrow{x}=\overrightarrow{A}+\lambda\cdot\overrightarrow{AB}+\mu\cdot\overrightarrow{AC}

Bemerkung: Das hätte mit $g$ auch funktioniert oder einem anderen Wert für den Parameter, diese Rechnung war lediglich die einfachste.

Diese drei Punkte werden in die Parameterform eingesetzt, indem die Verbindungsvektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ berechnet werden:

$\displaystyle E:~\overrightarrow{x}$	$=$	$\displaystyle \overrightarrow{A}+\lambda\cdot\overrightarrow{AB}+\mu\cdot\overrightarrow{AC}$
	↓	Einsetzen des Ortsvektors, Berechnen der Verbindungsvektoren
	$=$	$\displaystyle \begin{pmatrix}2\\3\\-1\end{pmatrix}+\lambda\cdot \begin{pmatrix}5-2\\-2-3\\0-(-1)\end{pmatrix}+\mu\cdot \begin{pmatrix}9-2\\-3-3\\-3-(-1)\end{pmatrix}$
	↓	Zusammenfassen
	$=$	$\displaystyle \begin{pmatrix}2\\3\\-1\end{pmatrix}+\lambda\cdot \begin{pmatrix}3\\-5\\1\end{pmatrix}+\mu\cdot \begin{pmatrix}7\\-6\\-2\end{pmatrix}$

Die Parameterform lässt sich dann auf die geforderte Darstellungsform umformen.

Ebenengleichung aufstellen aus schneidenden Geraden

Die beiden Geraden

\displaystyle E:~\overrightarrow{x}=\overrightarrow{A}+\lambda\cdot\overrightarrow{AB}+\mu\cdot\overrightarrow{AC}

besitzen einen gemeinsamen Schnittpunkt, wobei es nicht nötig ist, diesen zu wissen für das Aufstellen der Ebenengleichung. Für die Parameterform der Ebene wird ein Stützvektor gewählt, entweder der von $g$ oder $h$ und beide Richtungsvektoren als Spannvektoren.

Die Ebene ist damit direkt gegeben durch:

\displaystyle E:~\overrightarrow{x}=\overrightarrow{A}+\lambda\cdot\overrightarrow{AB}+\mu\cdot\overrightarrow{AC}

Übungsaufgaben

Inhalt wird geladen…

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Aufstellung von Ebenengleichung

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?