Subtrahiere die Vektoren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren subtrahieren
Komponentenweise Subtraktion:
Du subtrahierst die Vektoren voneinander, indem du ihre Koordinaten subtrahierst.
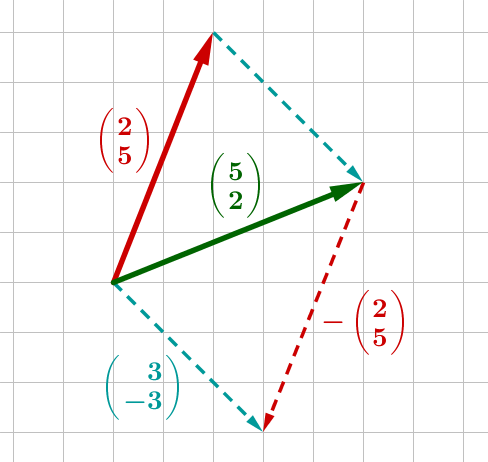
Graphische Subtraktion:
Den Lösungsvektor erhältst du, indem du den Gegenvektor des zweiten an die Spitze des ersten Vektors zeichnest.
Du siehst links auch, dass du den gleichen Vektor erhältst, wenn du die Spitzen der beiden Vektoren verbindest. Bei dieser Methode musst du allerdings aufpassen, in welche Richtung der Lösungsvektor zeigt.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren subtrahieren
Komponentenweise Subtraktion:
Du subtrahierst die Vektoren voneinander, indem du ihre Koordinaten subtrahierst.
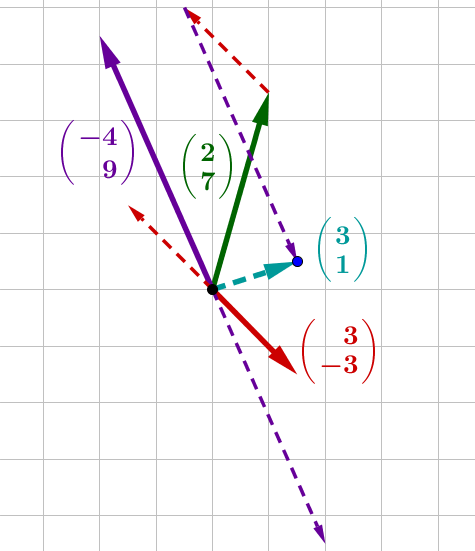
Graphische Subtraktion:
Den Lösungsvektor erhältst du, indem du den Gegenvektor des zweiten an die Spitze des ersten und den Gegenvektor des dritten an die Spitze dieses Vektors zeichnest.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren subtrahieren
Komponentenweise Subtraktion:
Du subtrahierst die Vektoren voneinander, indem du ihre Koordinaten subtrahierst.
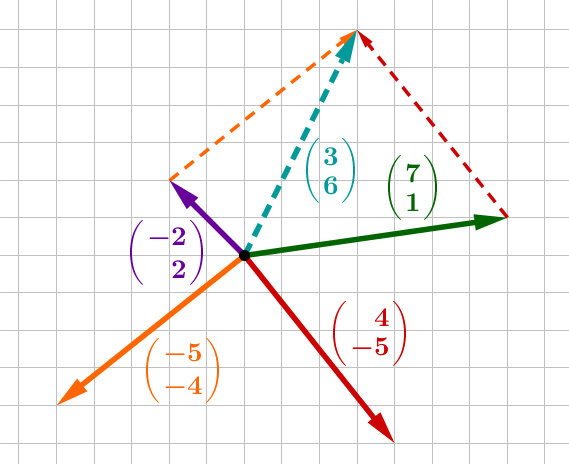
Graphische Subtraktion:
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
