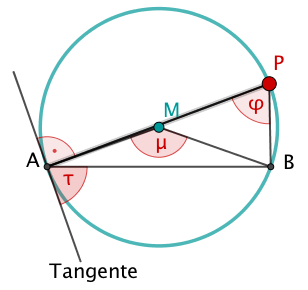
Beweiskunst
Der Punkt P liege auf dem Fasskreis der Sehne so, dass die Strecke Durchmesser ist.
Beweise für diese Lage von P den Randwinkelsatz, indem du zeigst, dass gilt:
.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Beweiskunst
Der Punkt P liege auf dem Fasskreis der Sehne so, dass die Strecke Durchmesser ist.
Beweise für diese Lage von P den Randwinkelsatz, indem du zeigst, dass gilt:
.
