Wenn man den Flächeninhalt einer zusammengesetzten Figur berechnen will, kann man ihn oft in bekannte Figuren aufteilen oder ergänzen und damit den Flächeninhalt leichter bestimmen.
Grundwissen: Flächeninhalt einfacher Figuren
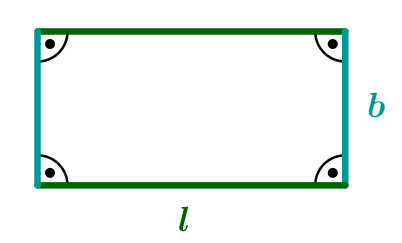
Den Flächeninhalt eines Rechtecks berechnet man, indem man die Länge mit der Breite multipliziert:
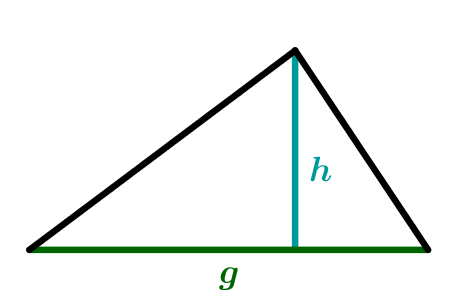
Den Flächeninhalt eines Dreiecks berechnet man, indem man die Grundseite mit der Höhe multipliziert und durch 2 dividiert:
Zerlegung in Rechtecke und Dreiecke
Schwierigere Figuren lassen sich manchmal in mehrere Rechtecke und/oder Dreiecke unterteilen. Mit diesem Trick kann man dann auch ihre Fläche einfach berechnen.
Beispiel
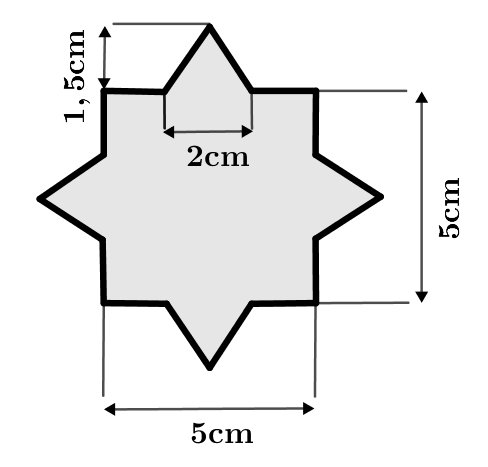
Um den Flächeninhalt dieser Figur zu bestimmen, kannst du zum Beispiel wie folgt vorgehen:
Überlege dir zuerst, in welche bekannten geometrischen Formen du die Figur zerlegen kannst.
Berechne nun den Flächeninhalt der bekannten Formen mit Hilfe der jeweiligen Formeln.
Den gesamten Flächeninhalt der Figur erhältst, indem du die Summe der berechneten Flächen addierst.
1.Bestimmung der bekannten Figuren:
Die Figur lässt sich beispielsweise in und zerlegen.
Beachte: Hier handelt es sich sogar um ein spezielles Rechteck und zwar um ein Quadrat!
2.Berechnung des Flächeninhalts der bekannten Figuren:
Die Fläche des Rechtecks lässt sich mit Hilfe der oben dargestellten Formeln und durch Einsetzen der entsprechenden Werte berechnen.
Die Fläche des Dreiecks lässt sich mit Hilfe der oben dargestellten Formel und durch Einsetzen der entsprechenden Werte berechnen.
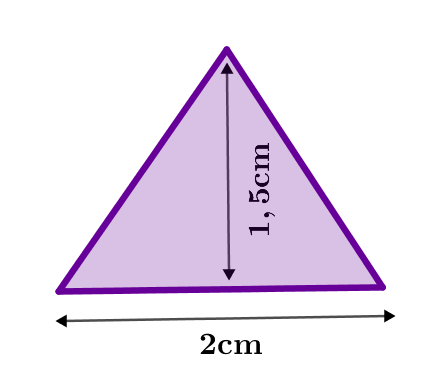
3.Flächeninhalt der gesamten Figur:
Die Summe der einzelnen Flächen liefert den Flächeninhalt der gesamten Figur.
Achtung: Es ist zu beachten, dass die Figur Dreiecke besitzt.
Der Flächeninhalte der Figur beträgt somit
Ergänzung zu einem Rechteck
Manchmal lässt sich der Flächeninhalt von schwierigen Figuren berechnen, indem man zuerst die Figur zu einer bekannten Form ergänzt und anschließend Formen, die nicht zu der Figur gehören, abzieht.
Beispiel
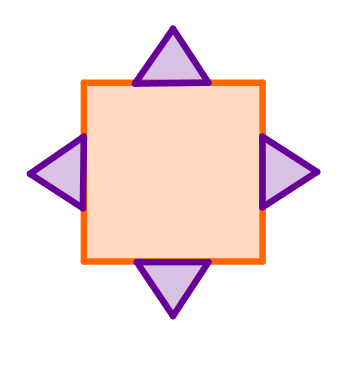
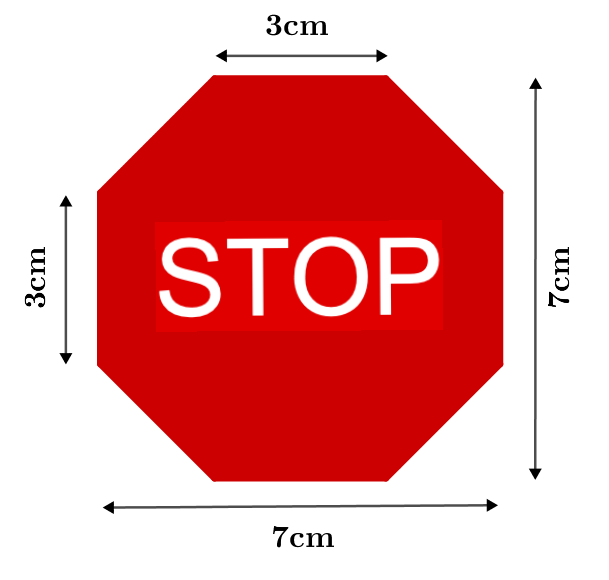
Um den Flächeninhalt dieser Figur (eines Achtecks) zu bestimmen, kannst du zum Beispiel wie folgt vorgehen:
Überlege dir zuerst zu welcher bekannten geometrische Form du die Figur ergänzen kannst.
Berechne nun den Flächeninhalt der bekannten Form mit Hilfe der entsprechenden Formel.
Bestimme die geometrischen Formen, die nicht zu der Figur gehören und ziehe diese von der ergänzten Form ab, um nur den Flächeninhalt der Figur zu erhalten.
1.Ergänzung zu einer bekannten Figur:
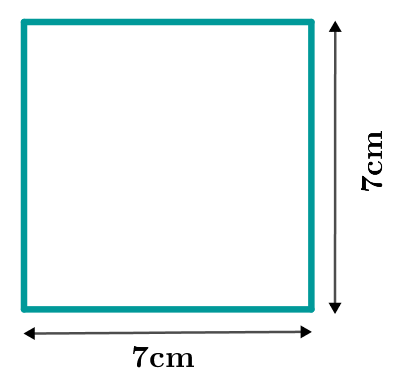
Die Figur lässt sich beispielsweise zu ergänzen.
Beachte: Hier handelt es sich sogar um ein spezielles Rechteck und zwar um ein Quadrat!

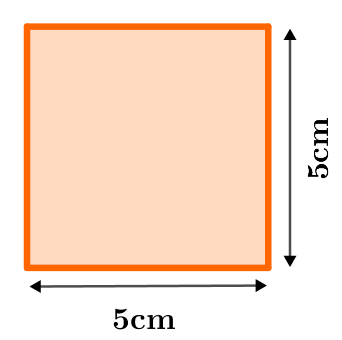
2.Berechnung des Flächeninhalts der bekannten Figur:
Die Fläche des Rechtecks lässt sich mit Hilfe der oben dargestellten Formeln und durch Einsetzen der entsprechenden Werte berechnen.
3.Abziehen der Formen, die nicht zur Figur gehören:
Um die Fläche der eigentlichen Figur zu erhalten, müssen wir noch die abziehen.
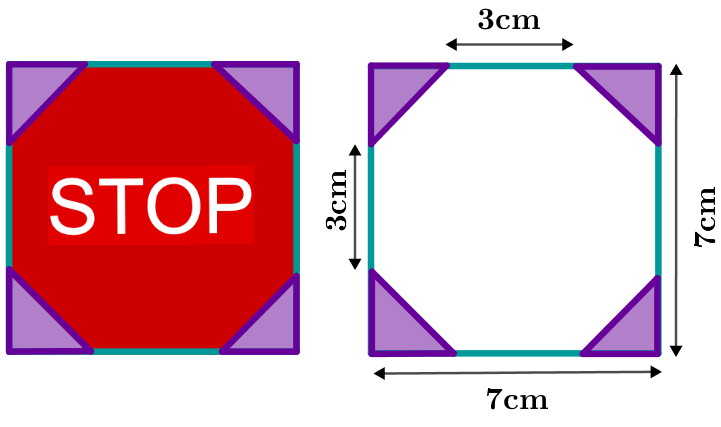
Die Fläche des Dreiecks lässt sich mit Hilfe der oben dargestellten Formel und durch Einsetzen der entsprechenden Werte berechnen. Dazu benötigt man die Grundseite und die Höhe des Dreiecks.
Bestimmung der Grundseite: Die Seitenlänge des Rechtecks beträgt und die Seite des Achtecks ist lang. Subtrahiert man die Seitenlänge des Achtecks von der Seitenlänge des Rechtecks, erhält man die Seiten von zwei Dreiecken.
Da es sich um zwei gleiche Dreiecke handelt, kann man die Seite von einem Dreieck bestimmen, indem man die durch dividiert.
Also ist die Grundseite des Dreiecks lang. Da es sich beim Rechteck um ein Quadrat handelt, sind alle Seiten gleich lang und somit sind alle Seiten der Dreiecke, die auf der Seite des Quadrats liegen, lang.
Bestimmung der Höhe: Betrachtet man die Dreiecke genauer, so erkennt man, dass es sich um rechtwinklige Dreiecke handelt. Das heißt die höhe beträgt ebenfalls .
Flächeninhalt des Dreiecks:
Flächeninhalt der gesamten Figur:
Abziehen der Dreiecke vom Rechteck, liefert uns den Flächeninhalt der gesamten Figur.
Achtung: Es ist zu beachten, dass Dreiecke abgezogen werden müssen.
Der Flächeninhalte der Figur beträgt somit .
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Flächenberechnung zusammengesetzter Figuren
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
