Mit Fasskreisbogen löst man die Frage, von wo aus man eine Strecke unter einem vorgegebenen Winkel sieht.
Fasskreisbogen erhalten ihre Bedeutung durch den sogenannten Randwinkelsatz. Man nennt diesen auch Umfangswinkelsatz oder Peripheriewinkelsatz.
Anwendung finden Fasskreisbogen bei Dreiecks- und Viereckskonstruktionen.
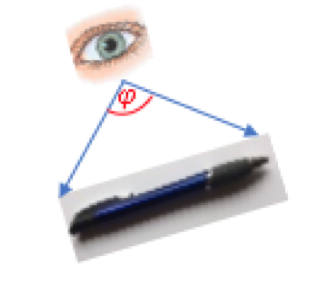
Aufgabe
Im nebenstehenden Applet ist eine Sehne des Kreises um .
Die Punkte , und sind verschiebbar. Klicke sie an und verschiebe sie!
a) Wie sind die Punkte in der Ebene verschiebbar?
b) Unter welchen Blickwinkeln erscheint die Sehne bei den verschiedenen Lagen der Punkte?
Ergebnisse:
a)
Der Punkt lässt sich beliebig in der Ebene verschieben. Der Punkt nur längs des oberen Kreisbogens. Der Punkt nur längs des unteren Kreisbogens.
b)
Die verschiedenen Punkte ergeben unterschiedliche Blickwinkel.
Der Blickwinkel eines Punktes vom oberen Kreisbogen beträgt dagegen stets . Der Blickwinkel eines beliebigen Punktes vom unteren Kreisbogen stets .
Es gilt:
Zusammenfassung des Applet-Experiments
Jeder der beiden Kreisbogen, in die die Sehne den Kreisumfang zerlegt, erfassen einen gleichen Blickwinkel.
Man spricht deshalb von den (beiden) Fasskreisbogen der Sehne.
Den jeweiligen Blickwinkel nennt man Randwinkel oder auch Umfangswinkel oder Peripheriewinkel.
Der Satz vom Thaleskreis
Ist die Sehne Durchmesser eines Kreises, so sind beide Fasskreisbogen Halbkreise und jeder erfasst einen Randwinkel von .
Von jedem Punkt eines Kreises erscheint jeder Durchmesser unter dem Blickwinkel von .
Ausnahmen: Die jeweiligen Endpunkte der Durchmesser.
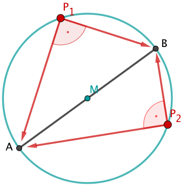
Der Randwinkelsatz
sei eine Sehne im Kreis , die kein Durchmesser ist. Dann gilt:
Alle Randwinkel des längeren Kreisbogens sind gleich groß.
Der Randwinkel ist halb so groß wie der Mittelpunktswinkel:
Der Randwinkel ist so groß wie der Sehnen-Tangentenwinkel:
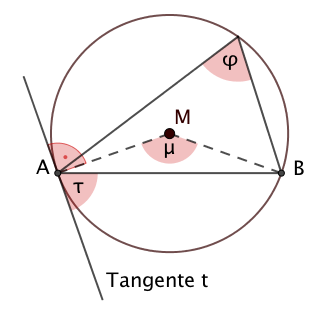
Für jedes Randwinkelmaß des kleineren Kreisbogens gilt:
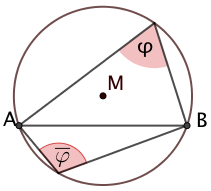
Das Fasskreisbogenpaar
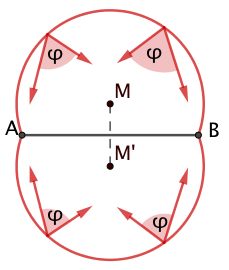
Der Randwinkelsatz besagt, dass eine Strecke von jedem Punkt seines Fasskreisbogens aus unter dem gleichen Blickwinkel erscheint.
Da sich die Größe eines Winkels bei Spiegelung an einer Geraden nicht ändert, bleibt der Blickwinkel auf die Strecke unverändert, wenn man den Fasskreisbogen an der Sehnengeraden spiegelt.
Das so erhaltene Fasskreisbogenpaar ist dann die Menge aller Punkte (der sogenannte "geometrische Ort"), von denen aus die Strecke unter dem vorgegebenen Winkel erscheint.
Fasskreisbogen konstruieren
Aufgabe
Konstruiere das Fasskreisbogenpaar zum Randwinkel .
Lösung:
Klicke im nachfolgenden Applet die einzelnen Konstruktionsschritte an.
Entscheidend ist schon im 1./2. Schritt die Konstruktion der Kreistangente im Punkt durch Antragen des Sehnen-Tangentenwinkels von . Das Lot zur Tangente führt zum Mittelpunkt des Fasskreises.
Fasskreisbogen anwenden
Aufgabe
Konstruiere ein Dreieck ABC aus dem Umkreisradius ; ; .
Lösung
Plan:
Das Teildreieck ist konstruierbar aus:und (Anwendung des Randwinkelsatzes!)
liegt dann
a) auf dem freien Schenkel von in an und
b) auf dem Kreis .
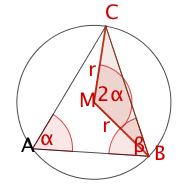
Beschreibung der Konstruktion:
Zeichne die Strecke mit .
Trage in an den Winkel an.
Der angetragene Schenkel schneidet den Kreis im Punkt .
Trage in an den Winkel an.
Der angetragene Schenkel schneidet den Kreis im Punkt .
Dreieck ist das gesuchte Dreieck.
Die Konstruktion kannst du im nebenstehenden Applet mit der Navigationsleiste (unten) schrittweise nachvollziehen.
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Fasskreisbogen und Satz des Thales
